Краткие теоретические сведения

ЭЛЕМЕНТЫТЕОРИИ МАССОВОГО ОБСЛУЖИВАНИЯ

 

 

Системы массового обслуживания (СМО) − это такие системы, в которых в случайные моменты времени поступают заявки на обслуживание, при этом поступившие заявки обслуживаются с помощью имеющихся в распоряжении системы каналов обслуживания. Примерами систем массового обслуживания могут служить: телефонные станции; ремонтные мастерские; отделы налоговых инспекций, занимающиеся приемкой и проверкой текущей отчетности предприятий; технические устройства, обслуживающие поступающие заявки и т. д. В качестве каналов обслуживания могут фигурировать: линии связи; лица, выполняющие те или иные операции; различные приборы и т. п.

Предмет теории массового обслуживания − установление вероятностных зависимостей между потоками заявок и обслуживающими их каналами. На практике обычно моменты поступления заявок случайны. В связи с этим процесс работы системы протекает нерегулярно: в потоке заявок образуются местные сгущения и разрежения. Сгущения могут привести либо к отказам в обслуживании, либо к образованию очередей. Разрежения − к непроизводительным простоям отдельных каналов или системы в целом. На эти случайности, связанные с неоднородностью потока заявок, накладываются еще случайности, связанные с задержками обслуживания отдельных заявок. Таким образом, процесс функционирования системы массового обслуживания представляет собой случайный процесс.

Поток событий. Простейший поток. Потоком событий называется последовательность однородных событий, следующих одно за другим через какие-то, вообще говоря, случайные интервалы времени. Например, поток вызовов на АТС, поток прибывающих на нижний склад машин с хлыстами и т. д. Такой поток можно изобразить как ряд точек на оси времени (рис. 7.1).

Рис. 1. Схема простейшего потока событий

 

Поток событий называется регулярным,если события следуют одно за другим через строго определенные промежутки времени. В реальных системах встречается сравнительно редко.

Важной характеристикой потока является его интенсивность − среднее число событий, приходящихся на единицу времени. Интенсивность потока может быть как постоянной, так и переменной, зависящей от времени: . Например, поток машин, движущихся по улице днем, интенсивнее, чем ночью; в часы «пик» интенсивнее, чем в другое время.

Поток называется стационарным, если его вероятностные характеристики не зависят от времени. В частности, интенсивность стационарного потока должна быть постоянной. Это, однако, не означает, что фактическое число событий, появляющихся в единицу времени, постоянно, поток неизбежно имеет точки сгущения и разрежения.

Поток событий называется потоком без последействия, если для любых двух непересекающихся участков времени и число событий, попадающих на один из них, не зависит от того, сколько событий попадает на другой (рис. 2).

Рис. 2. Схема потока событий без последействия

 

Условие отсутствия последействия означает, что заявки поступают в систему независимо друг от друга.

Поток событий называется ординарным, если события в нем появляются поодиночке, а не группами. Например, поток поездов ординарен, поток прибывающих вагонов в поезде неординарен.

Поток событий называется пуассоновским,если обладает двумя свойствами − ординарностью и отсутствием последействия. Стационарный пуассоновский поток событий называется простейшим.

В расчетах, связанных с потоками случайных событий, удобно пользоваться понятием «элемента вероятности». Рассмотрим на оси простейший поток с интенсивностью и произвольно расположенный элементарный участок времени . Элементом вероятности называется вероятность попадания на этот участок хотя бы одного события потока. Для простейшего потока элемент вероятности с точностью до малых более высокого порядка малости по сравнению с равен .

Понятие марковского процесса. Случайный характер потока заявок, а также в общем случае длительности обслуживания приводит к тому, что в системе массового обслуживания происходит случайный процесс: система в случайные моменты времени переходит из одного состояния в другое.

По характеру случайного процесса различают системы марковские и немарковские. В марковских системах входящий поток заявок и выходящий поток обслуженных заявок являются пуассоновскими. Пуассоновские потоки позволяют легко описать и построить математическую модель системы массового обслуживания. Данные модели имеют достаточно простые решения, поэтому большинство известных приложений теории массового обслуживания используют марковскую схему.

Случайный процесс, протекающий в системе S, называется марковским, если для любого момента времени вероятностные характеристики системы в будущем (при ) зависят только от ее состояния в момент и не зависят от того, как система S пришла в это состояние. Другими словами, для марковского процесса«будущее» можно «предсказать», учитывая только «настоящее» состояние системы без ее «предыстории».

Важное место среди случайных процессов занимают марковские случайные процессы с дискретными состояниями и непрерывным временем. Процесс называется процессом с дискретными состояниями, если его возможные состояния 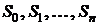можно перечислить (пронумеровать) и переход системы из состояния в состояние происходит «скачком», т. е. практически мгновенно. Процесс называется процессом с непрерывным временем, если моменты возможных переходов из состояния в состояние не фиксированы заранее, а случайны, т. е. переход может осуществиться в принципе в любой момент. Будем считать, что все переходы системы из одного состояния в другое осуществляются под действием потоков событий (поток поломок раскряжевочной машины, поток прибывающих лесовозов и т. д.).

Для процессов с дискретными состояниями и непрерывным временем справедливо следующее утверждение: для того чтобы процесс, протекающий в системе, был марковским, необходимо и достаточно, чтобы все потоки событий, переводящие систему из состояния в состояние, были пуассоновскими.

В качестве примера рассмотрим работу раскряжёвочной установки. Для процесса раскряжевки характерны следующие состояния:

− установка осуществляет раскряжевку хлыстов;

− установка исправна и свободна (простаивает из-за отсутствия хлыстов);

− установка неисправна.

Этот процесс является дискретным (три состояния 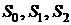) с непрерывным временем. Мы не можем заранее точно указать момент, когда установка испортится или привезут хлысты.

При анализе случайных процессов с дискретными состояниями удобно пользоваться геометрической схемой − так называемым графом состояний. Возможные состояния обозначаются прямоугольниками (кругами), а возможные переходы − стрелками. Так, в рассматриваемом примере граф состояний будет иметь вид, представленный на рис. 3.

Рис. 3. Граф состояний раскряжевочной установки

 

Раскряжевочная установка из состояния может перейти в состояние или или наоборот из состояний и − в состояние . В то же время мы видим, что из состояния (установка неисправна) установка может перейти в состояние (установка исправна, но не работает), а перейти из состояния в состояние она не может.

Уравнения Колмогорова для вероятностей состояний. Рассмотрим математическое описание марковского случайного процесса с дискретным состоянием и непрерывным временем.

Пусть система характеризуется состояниями 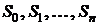, а переход из состояния в состояние может осуществиться в любой момент времени. И пусть все переходы системы S из состояния в состояние (стрелка на графе состояний направлена из в ) происходят под действием каких-либо простейших потоков событий с интенсивностями ,

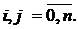
Для наглядности на графе состояний у каждой стрелки проставим интенсивность потока событий, который переводит систему по данной стрелке. Такой граф состояний называется размеченным. Так, размеченный граф работы раскряжеочной установки показан на рис. 4.

Рис. 4. Размеченный граф состояний раскряжёвочной установки

 

Здесь 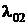− интенсивность потока отказов установки; 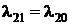− интенсивность потока восстановлений установки; 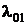− интенсивность потока расходования хлыстов; − интенсивность поступления хлыстов.

Обозначим через вероятность того, что в момент времени t система S будет находиться в состоянии . Очевидно, что

. (1)

Имея размеченный граф состояний, можно найти все вероятности как функции времени. Для этого составляются дифференциальные уравнения Колмогорова, в которых неизвестными являются вероятности состояний. Уравнения Колмогорова удобно составлять, пользуясь размеченным графом состояний и следующим мнемоническим правилом.

Правило. Чтобы записать уравнение Колмогорова для i- го состояния, нужно в левой части уравнения записать производную 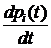; в правой части уравнения − сумму произведений вероятностей всех состояний, из которых идут стрелки в данное состояние, на интенсивность соответствующих потоков минус суммарная интенсивность всех потоков, выводящих систему из данного состояния, умноженная на вероятность данного i -го состояния.

Таким образом, каждому из состояний S ₀, S ₁, …, S_n соответствует линейное дифференциальное уравнение, а для всех состояний получаем систему из n линейных дифференциальных уравнений с n неизвестными (одно из них, любое, можно отбросить, пользуясь тем, что Р ₀(t) + Р ₁(t) + …+ Р_n (t) = 1).

Чтобы решить систему уравнений Колмогорова, нужно задать начальные условия. Так, если мы точно знаем, что в начальный момент t = 0 система находилась в состоянии S_i, то начальные условия имеют вид Р_i (0) = 1; Р_j (0) = 0, i ¹ j.

Так, уравнения Колмогорова в примере с раскряжевочной установкой (см. рис. 4) будут представлены системой

Дифференциальные уравнения Колмогорова составляются для марковских процессов с непрерывным временем.

Финальные вероятности состояний. Если процесс, протекающий в системе, длится достаточно долго, то имеет смысл говорить о предельном поведении вероятностей при . Если существуют пределы вероятностей состояний , при и эти пределы не зависят от первоначального состояния системы, то они называются финальными вероятностями системы. Это означает, что с течением времени в системе S устанавливается предельный стационарный режим, в ходе которого она переходит из состояния в состояние, но вероятности состояний уже не меняются. В этом предельном режиме каждая финальная вероятность может быть истолкована как среднее относительное время пребывания системы в данном состоянии. Система, для которой существуют финальные вероятности, называется эргодической, а соответствующий случайный процесс − эргодическим.

Если система имеет конечное число состояний S ₀, S ₁, …, и все потоки событий, переводящие систему из состояния в состояние простейшие (свойство однородности), то для существования финальных вероятностей достаточно, чтобы из любого состояния системы можно было найти путь, по которому можно добраться до любого другого состояния и вернуться в исходное состояние (свойство транзитивности).

Поскольку финальные вероятности постоянны, то производные от них равны нулю и система уравнений Колмогорова преобразуется в систему алгебраических уравнений. Решив эту систему, получаем финальные вероятности.

Таким образом, для системы S с состояниями 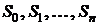получается система линейных однородных алгебраических уравнений с неизвестными . Для нахождения точного значения к уравнениям добавляют нормировочное условие (1), пользуясь которым можно выразить любую из вероятностей через другие и отбросить одно из уравнений.

 

Примеры решения задач

 

Задача. Техническое устройство может находиться в одном из трех состояний 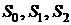. Интенсивности потоков, которые переводят устройство из одного состояния в другое, известны: 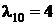, , Необходимо построить размеченный граф состояний, записать систему дифференциальных уравнений Колмогорова, найти финальные вероятности состояний и проанализировать полученное решение.

Решение.

Размеченный граф состояний представлен на рис. 5.

Рис. 5. Размеченный граф состояний

 

По графу запишем систему уравнений Колмогорова в общем виде:

 

Вместо интенсивностей потоков подставим их конкретные значения и получим искомую систему

Чтобы найти финальные вероятности состояний, в уравнениях Колмогорова отбросим первое уравнение, а по остальным составим систему алгебраических уравнений:

Решая эту систему, получим

Вывод. При достаточно большом времени работы техническое устройство с вероятностью будет находиться в состоянии , с вероятностью − в состоянии и с вероятностью − в состоянии .