Лекция №157
Тема: Последовательности.
Цель:
Учебная:
- познакомить обучающихся с последовательностями и их свойствами;
Развивающая:
- формирование умений применять приемы сравнения, обобщения, выделения главного, логически излагать мысли, делать выводы, развивать речь, внимание и память.
Воспитательная:
- способствовать формированию умений применять приемы: сравнения, обобщения, выявления главного, переноса знаний в новую ситуацию, развитию математического кругозора, мышления и речи, внимания и памяти.
Методы обучения: практическая работа, контрольная работа.
Оборудование: компьютер, проектор.
Тип урока: урок обобщения и систематизации знаний.
Формируемые на уроке ПК и ОК
ОК 2. Организовывать собственную деятельность, выбирать типовые методы и способы выполнения профессиональных задач, оценивать их эффективность и качество.
ОК 4. Осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач, профессионального и личностного развития.
План урока.
1. Организационный момент.
2. Что такое последовательность и чем она отличается от обычной функции?
3. Зачем рассматривают пределы последовательностей?
4. Почему надо доказывать существование предела?
5. Задание на дом.
6. Подведение итогов.
Ход занятия.
1. Организационный момент – приветствие, проверка посещаемости.
Занятие 2 Последовательности
Что такое последовательность и чем она отличается от обычной функции?
1. Последовательность как функция. Последовательность можно понимать как частный вид функции. Числовая последовательность определяется пра-вилом, по которому для всякого натурального числа n можно вычислить n -й член этой последовательности. Таким образом, областью определения последовательности как функции является множество N натуральных чисел. Значением этой функции является число. Если функцию обозначить буквой f, то её значение в точке n запишется как f (n). Однако для последовательностей традиционно выбирается другое обоз-начение – члены последовательности обозначаются малыми латинскими буквами – a, b, c и т.д., а значение аргумента n пишется в виде индекса: an, bn, cn и т.д.
|
|
Главная особенность последователь-ности состоит в том, что значения аргумента (номера членов последова-тельности) расположены друг за другом, и их можно перебирать, двигаясь от одного номера к следующему. Это позволяет использовать особый способ задания последовательности, который неприменим к функции общего вида и называется рекуррентным. При обычных способах задания функции можно взять любое
Числовые
последовательности
1. 1, 2, 3, 4, 5, … an = n.
2. 1, 4, 9, 16, 25, … an = n 2
3. 1, 2, 4, 8, 16, … an = 2 n -1
4. 1,  ,
,  ,
,  , … an =
, … an = 
5.  ,
,  ,
,  ,
,  , … an =
, … an = 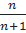
6.  ,
,  ,
, 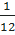 ,
, 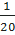 , … an =
, … an = 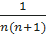
Общий член
последовательности
an
Последовательность сумм
{ an } – данная последовательность
{ sn } – последовательность сумм
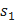 =
= 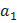
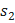 =
= 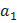 +
+ 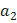
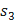 =
= 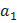 +
+ 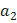 +
+ 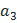
……….
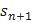 = sn +
= sn + 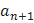
Примеры значение аргумента и для него найти соот-




Правила вычисления найти число С такое, что an ≤ С при всех n.




Итак, 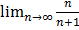 = 1, что мы, и Sn < S. Это означает, что последовательно-
= 1, что мы, и Sn < S. Это означает, что последовательно-


грессия со знаменателем q = 0,01
Применяем формулу:
2 + 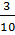 +
+ 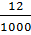 ∙
∙ 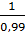 =
=
= 2 + 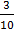 +
+ 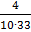 = 2 +
= 2 + 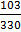 =
= 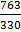
an > 0, то его можно возвести в квадрат и по-лучить для проверки неравенство a 2 – an – 2 < 0. Решив неравенство х 2 – х – 2 < 0, получим промежуток (–1; 2), в котором лежат числа последовательности (0 < an < 2). Существование предела полностью доказано.
|
|
Домашнее задание
Учебник Башмакова (О-1), стр. 165-171
Учебник Никольского, 11 класс (Д-3), §2.1
Итог урока
Обучающиеся отвечают на вопросы, что они сегодня изучили, что было понятно, а что нет.