Призмы встречающиеся в жизни

Тема: Наклонная, прямая и правильная призма.

Задание: изучить теоретические основы темы по конспекту или учебнику (Геометрия. Учебник для 10-11 классов - Атанасян Л.С., глава III, § 1, п. 30), законспектировать 2 задачи на сечения призмы, решить задачи самостоятельной работы и ответить письменно на контрольные вопросы.

Теоретический минимум и задачи

Призмы встречающиеся в жизни

Определение: Многогранник, составленный из двух равных многоугольников А₁А₂…А_n и В₁В₂…В_n, расположенных в параллельных плоскостях, и n параллелограммов, называется призмой.

А₁А₂…А_n В₁В₂…В_n - n-угольная призма.

Многоугольники А₁А₂…А_n и В₁В₂…В_n – основания призмы.

Параллелограммы А₁В₁В₂В₂, А₂В₂В₃А₃ и т.д. боковые грани призмы

 

Название призмы происходит из названия её основания.

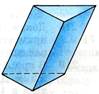
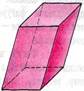
Шестиугольная призма	Треугольная призма	Четырехугольная призма

Высотой призмы называется отрезок, являющийся общим перпендикуляром плоскостей, в которых лежат основания призмы.

Высота призмы равна расстоянию h между плоскостями оснований

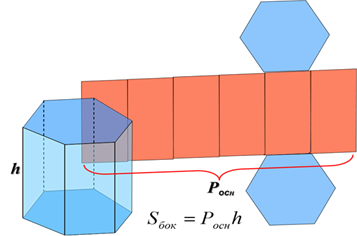Поверхность призмы состоит из двух оснований и боковой поверхности. С помощью развёртки призмы рассмотрим площадь её поверхности. 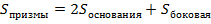. Площадь основания зависит от многоугольника в основании призмы. Для боковой поверхности можно вывести общую формулу.

 

 

 

Виды призм.

Если боковые ребра перпендикулярны к основаниям, то призма называется прямой,

в противном случае наклонной.

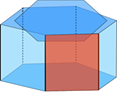Высота прямой призмы равна ее боковому ребру.

 

Призма называется правильной, если она прямая и ее основания - правильные многоугольники..

 

 

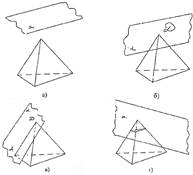
Сечения призмы.

Задача состоит в построении пересечения двух фигур: многогранника и плоскости (рис.1). Это могут быть: пустая фигура (а), точка (б), отрезок (в), многоугольник (г). Если пересечение многогранника и плоскости есть многоугольник, то этот многоугольник называется сечением многогранника плоскостью.

 

Рис. 1

Будем рассматривать только случай, когда плоскость пересекает многогранник по его внутренности. При этом пересечением данной плоскости с каждой гранью многогранника будет некоторый отрезок. Таким образом, задача считается решенной, если найдены все отрезки, по которым плоскость пересекает грани многогранника.

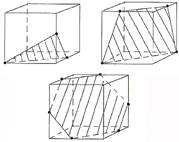
Исследуйте сечения куба (рис.2) и ответьте на следующие вопросы:

- какие многоугольники получаются в сечении куба плоскостью? (Важно число сторон многоугольника). Чему равно наибольшее число сторон многоугольника, полученного сечением многогранника с плоскостью?

Рис. 2

Методы построения сечений

) а) Метод следов заключается в построении следов секущей плоскости на плоскость каждой грани многогранника. Построение сечения многогранника методом следов обычно начинают с построения так называемого основного следа секущей плоскости, т.е. следа секущей плоскости на плоскости основания многогранника.

б) Метод вспомогательных сечений построения сечений многогранников является в достаточной мере универсальным. В тех случаях, когда нужный след (или следы) секущей плоскости оказывается за пределами чертежа, этот метод имеет даже определенные преимущества. Вместе с тем следует иметь ввиду, что построения, выполняемые при использовании этого метода, зачастую получаются “скученными”. Тем не менее в некоторых случаях метод вспомогательных сечений оказывается наиболее рациональным.

Метод следов и метод вспомогательных сечений являются разновидностями аксиоматического метода построения сечений многогранников плоскостью.

в) Суть комбинированного метода построения сечений многогранников состоит в применении теорем о параллельности прямых и плоскостей в пространстве в сочетании с аксиоматическим методом.

Задача 1.

Построить сечение призмы ABCDA₁B₁C₁D₁ плоскостью, проходящей через точки P, Q, R (точки указаны на чертеже (рис.3)).

Решение.

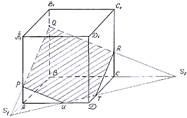
Рис. 3

1. Построим след секущей плоскости на плоскость нижнего основания призмы. Рассмотрим грань АА₁В₁В. В этой грани лежат точки сечения P и Q. Проведем прямую PQ.
2. Продолжим прямую PQ, которая принадлежит сечению, до пересечения с прямой АВ. Получим точку S₁, принадлежащую следу.
3. Аналогично получаем точку S₂ пересечением прямых QR и BC.
4. Прямая S₁S₂ - след секущей плоскости на плоскость нижнего основания призмы.
5. Прямая S₁S₂ пересекает сторону AD в точке U, сторону CD в точке Т. Соединим точки P и U, так как они лежат в одной плоскости грани АА₁D₁D. Аналогично получаем TU и RT.
6. PQRTU – искомое сечение.

Задача 2.

Построить сечение параллелепипеда ABCDA₁B₁C₁D₁ плоскостью, проходящей через точки M, N, P (точки указаны на чертеже (рис.4)).

Решение.

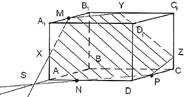
Рис. 4

1. Точки N и P лежат в плоскости сечения и в плоскости нижнего основания параллелепипеда. Построим прямую, проодящую через эти точки. Эта прямая является следом секущей плоскости на плоскость основания параллелепипеда.
2. Продолжим прямую, на которой лежит сторона AB параллелепипеда. Прямые AB и NP пересекутся в некоторой точке S. Эта точка принадлежит плоскости сечения.
3. Так как точка M также принадлежит плоскости сечения и пересекает прямую АА₁ в некоторой точке Х.
4. Точки X и N лежат в одной плоскости грани АА₁D₁D, соединим их и получим прямую XN.
5. Так как плоскости граней параллелепипеда параллельны, то через точку M можно провести прямую в грани A₁B₁C₁D₁, параллельную прямой NP. Эта прямая пересечет сторону В₁С₁ в точке Y.
6. Аналогично проводим прямую YZ, параллельно прямой XN. Соединяем Z с P и получаем искомое сечение – MYZPNX.

Самостоятельная работа

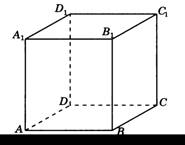
Задача 1 Дано: правильная четырёхугольная призма, ABCD. АВ=3см, АА₁ = 5см. Найти: Диагональ основания, диагональ боковой грани, диагональ призмы, площадь основания, площадь диагонального сечения, площадь боковой поверхности, площадь поверхности призмы.

 

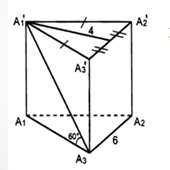
Задача 2 Дано: прямая треугольная призма.

Найти высоту призмы и площадь её боковой поверхности.

Контрольные вопросы:

1. Какой многогранник называется призмой?

2. Какая призма называется прямой?

3. Какая призма называется правильной?

4. Какое наименьшее число ребер, граней и вершин может иметь призма?

5. Сколько диагоналей призмы можно провести в четырехугольной призме, в треугольной призме?