Основные требования к алгоритмам(Вычегжанин)

ТЕОРИЯ АЛГОРИТМОВ

Основные понятия

Основные требования к алгоритмам(Вычегжанин)

С алгоритмами, т.е. эффективными процедурами, однозначно приводящими к результату, математика имела дело всегда.

Например: школьные методы умножения столбиком, деление углом многозначных чисел, метод исключения неизвестных при решении системы линейных уравнений, правило дифференцирования сложной функции – это все алгоритмы. Понятие метода вычисления считалось изначально ясным и не нуждалось в специальных исследованиях. Одним из решающих обстоятельств, приведших к пересмотру оснований математики, т.е. принципов, лежащих в основе математических рассуждений, явилось создание Кантором теории множеств. Довольно быстро стало ясно, что некоторые, кажущиеся вполне естественными рассуждения, в рамках этой теории приводят к неразрешимым противоречиям – парадоксам теории множеств. Это потребовало точного изучения принципов математических рассуждений математическими же средствами. Возникла особая отрасль математики – метаматематика.

Опыт парадоксов теории множеств научил математику крайне осторожно обращаться с бесконечностью и по возможности даже о бесконечности рассуждать с помощью финитных методов. Существо финитного подхода заключается в том, что он допускает только конечные комплексы действий над конечным числом объектов. Выяснение того, какие объекты и действия над ними следует считать точно определенными, какими свойствами и возможностями обладают комбинации действий, что можно и чего нельзя сделать с их помощью - все это стало предметом теории алгоритмов и формальных систем. Главным приложением теории алгоритмов внутри самой математики явились доказательства невозможности алгоритмического (т.е. точного и однозначного) решения некоторых математических проблем. Пока техника использовала чисто вычислительные методы, эти высокие проблемы чистой математики ее мало интересовали. В технику термин "алгоритм" пришел вместе с кибернетикой. Понадобилось осознавать, каким требованиям должна удовлетворять последовательность действий, чтобы считаться эффективно заданной.

С точки зрения современной практики алгоритм – это программа, а критерием алгоритмичности процесса является возможность его запрограммировать. Именно благодаря этой реальности алгоритма, понятие алгоритма в технике стало популярным за весьма короткий срок. В повседневной практике слово "алгоритм" употребляется слишком широко, теряя зачастую свой точный смысл В результате за алгоритм выдается любая инструкция, разбитая на шаги.

То есть алгоритм – это однозначно трактуемая процедура, осуществляемая черным ящиком для получения выхода из входа. Этим черным ящиком может быть вычислительная машина, человек или устройство. Процедура – это конечная последовательность точно опре-деленных шагов или операций, для выполнения каждой из которых требуется конечный объем оперативной памяти и конечное время. Одно из неудобств этого определения состоит в том, что термин "однозначная трактовка" весьма неоднозначен. Ничто не является абсолютно ясным или абсолютно неясным, должен быть указан, хотя бы неявно, исполнитель. Алгоритм вычисления производной кубического полинома вполне ясен тем, кто знаком с анализом, но для прочих совершенно непонятен. Может случиться, что алгоритм существует для конкретной задачи, но его трудно или невозможно описать в некоторой заданной форме. Человечество разработало эффективный алгоритм завязывания шнурков на ботинках. Но дать чисто словесное описание такого алгоритма без картинок и демонстрации очень трудно.

Чтобы создать алгоритм необходимо знать:

1. какую работу должен выполнять алгоритм.

2. какими должны быть входные данные.

3. какими должны быть выходные данные.

Даже если не следовать реальному методу построения алгоритмов, нужно четко понимать, что алгоритм будет получать входные данные и преобразовывать их, чтобы создать требуемые выходные данные. Затем следует решить, в каком порядке должны выполняться отдельные процессы, и наконец, надо решить, какие отдельные процессы будут взаимодействовать между собой, а какие зависят от тех или иных других процессов.

Рассмотрим некоторые основные принципы, по которым строятся алгоритмы, и выясним, что же именно в понятии алгоритма нуждается в уточнении.

Первое, что следует отметить в любом алгоритме – это то, что он применяется к исходным данным и выдает результаты. В технических терминах это означает, что алгоритм имеет входы и выходы.

Кроме того, в ходе работы алгоритма появляются промежуточные результаты, которые используются в дальнейшем. Т.о. каждый алгоритм имеет дело с данными – входными, промежуточными и выходными.

Термин "данные" относится к формализованному представлению информации. Данные могут состоять из файлов информационных записей в виде "битов" (единиц и нулей) или же могут иметь форму одинаковым образом оцифрованной информации.

Поскольку мы собираемся уточнять понятие алгоритма, нужно уточнить и понятие данных, то есть указать, каким требованиям должны удовлетворять объекты, чтобы алгоритм мог с ними работать. Ясно, что эти объекты должны быть четко определены и отличимы как друг от друга, так и от "необъектов".

Все данные до некоторой степени подвержены воздействиям человеческой непоследовательности, вкрадываются ошибки.

В теории алгоритмов фиксируют конкретные конечные наборы исходных объектов (называемые элементарными) и конечный набор средств построения объектов из элементарных. Набор элементарных объектов образует конечный алфавит исходных символов (цифр, букв, и т.д.) из которых строятся другие объекты; типичным средством построе­ния являются индуктивные определения, указывающие, как строить новые объекты из уже построенных.

Например, в АЛГОЛе определение идентификатора дано следующим образом: идентификатор – это либо буква, либо идентификатор, к которому приписана справа буква или цифра.

Слова конечной длины (например, числа) – наиболее обычный тип алгоритмических данных, а число символов в слове – естественная единица измерения объема обрабатываемой информации. Более слож­ный случай алгоритмических объектов – формулы. Они также опреде­ляются индуктивно и также являются словами в конечном алфавите, однако не каждое слово в этом алфавите является формулой. В этом случае перед основным алгоритмом идут вспомогательные, которые проверяют, удовлетворяют ли исходные данные нужным требованиям. Такая проверка называется синтаксическим анализом.

Второе, данные для своего размещения требуют памяти. Память обычно считается однородной и дискретной, то есть состоит из одина­ковых ячеек, причем каждая ячейка может содержать один символ алфа­вита данных. Т.о. единицы измерения объема данных и памяти согла­сованы. При этом память может быть бесконечной.

Третье, алгоритм состоит из отдельных элементарных шагов, причем множество различных шагов, из которых составлен алгоритм – конечно. Обычно элементарный шаг имеет дело с фиксированным числом символов, однако это требование не всегда выполняется.

Четвертое, последовательность шагов алгоритма детерминирована, т.е. после каждого шага указывается, какой шаг делать дальше, либо дается команда останова, после чего работа алгоритма считается законченной.

Пятое, естественно для алгоритма потребовать результативности, т.е. остановки после конечного числа шагов с указанием того, что считать результатом. Однако, проверить результативность (сходимость) гораздо труднее, чем предыдущие требования. Сходимость обычно не удается установить простым просмотром алгоритма. Общего метода проверки сходимости пригодного для любого алгоритма и любых данных вообще не существует.

Шестое, следует различать:

описание алгоритма (программу);

механизм реализации, включающий средства пуска,останова, реализации элементарных шагов, выдачи результатов и обеспечения управления ходом вычисления (ЭВМ);

процесс реализации алгоритма, то есть последо­вательность шагов, которая будет порождена при применении алгоритма к конкретным данным.

(Набиулин)

Например: рассмотрим следующую задачу: дана последо­вательность Р из n положительных чисел (n – конечное, но произвольное число); требуется упорядочить их, то есть построить последовательность R, в которой эти же числа распололжены в порядке возрастания.

Простейший способ, который приходит в голову: просматриваем Р и находим наименьшее число; вычеркиваем его из Р и выписываем его как первое число R; снова просматриваем Р и находим наименьшее число, приписываем его справа к R и т.д., пока в Р не будут вычеркнуты все числа.

Возникает вопрос, что значит "и т.д.". Перепишем описание в более четкой форме, с указанием переходов между шагами.

Шаг 1. Ищем в Р наименьшее число.

Шаг 2. Найденное число записываем справа к R и вычеркиваем из Р.

Шаг 3. Если в Р нет чисел, переходим к шагу 4, иначе переходим к шагу 1.

Шаг 4. Конец. Результатом считать последовательность R, построенную к этому моменту.

Большинство сочтет описание достаточно ясным, чтобы пользуясь им, однозначно получить нужный результат. Это впечатление опирается на некоторые неявные предположения, к правильности которых мы привыкли, но которые нетрудно нарушить: что значит "дана последо­вательность чисел"? Является ли таковой запись 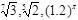? Очевидно, да, но в описании не сказано, как найти наименьшее среди таких чисел. В нем вообще не говорится о том, как искать наименьшие числа. Предполагается, что речь идет о числах, представленных в виде десятичных дробей и известно, как их сравнивать. Необходимо уточнить формы представления данных. При этом нельзя заявить, что допустимо любое представление чисел. Ведь для каждого представления существует свой алфавит (который помимо цифр может включать запятые, скобки, знаки операций и функций) и свой способ сравнения чисел (например, способ перевода в десятичную дробь). Представление чисел в виде десятичных дробей тоже не решает всех проблем. Сравнение 10-20–и разрядных чисел уже не может считаться элементарным действием: попробуйте сразу сказать, какое число больше 90811557001,15 или 32899901467,0048.

В машинных алгоритмах само представление числа еще требует дальнейшего уточнения: нужно ограничить число разрядов в числе, ведь от этого зависит, сколько ячеек памяти будет занимать число, договориться о способе размещения десятичной запятой в числе (с фиксированной или с плавающей запятой), поскольку способы обработки этих представлений различны. Наконец, на шаге 1 требуется узнать две вещи: само число (чтобы записать его в R) и его место в Р, т.е. адрес в той части памяти, где хра­нится Р (чтобы вычеркнуть его из Р), а следовательно, нужно иметь средства указания этого адреса. Таким образом, даже в этом простом примере описанию, которое выглядит вполне ясным, еще далеко до алгоритма.

В этом примере мы столкнулись с необходимостью уточнить почти все основные характеристики алгоритма, которые отмечались ранее: алфавит данных и форму их представления, память и размещение в ней элементов, элементарные шаги. Кроме того, выбор механизма реализации (человек или ЭВМ) будет влиять и на сам характер уточнения: у человека требования к памяти, представлению данных и к элементарности шагов гораздо более слабые и "укрупненные". В приведенном описании только два требования выполнены в достаточной мере: довольно очевидна сходимость алгоритма (после шагов 1 и 2 либо работа заканчивается, либо из Р вычеркивается число, поэтому после n выполнений 1 и 2 шагов алгоритм остановится) и не вызывает сомнения детерминированность: если учесть общепринятое соглашение – если шаг не содержит указаний о дальнейшем переходе, выполняется шаг, следующий за ним в описании.

Блок–схемы алгоритмов

Связи между шагами можно изобразить в виде графа:

Такой граф, в котором вершинам соответствуют шаги, а ребрам – переходы между шагами, называется блок-схемой алгоритма. Его вершины могут быть двух видов:

1) из которой выходит одно ребро – операторы;

2) из которой выходит два ребра – логические условия или предикаты.

Кроме того, имеется единственный оператор конца (из которого не выходит ни одного ребра) и единственный оператор начала. Важной особенностью блок-схем является то, что связи которые она описывает, не зависят от того, являются ли шаги элементарными или представляют собой самостоятельные алгоритмы – блоки. Для данного блока неважно, как устроены другие блоки; для программирования блока достаточно знать, где лежит исходная информация, какова форма её предcтавления, что должен делать блок и куда записывать результат. Блок-схемы соответствуют логике, которой пользуется программист для создания сложных, многовариантных, итеративных планов действий.

При всей наглядности языка блок-схем не следует переоценивать его возможности. Он отражает связи лишь по управлению. Блок-схемы не содержат сведений ни о данных, ни о памяти, ни о используемом наборе элементарных шагов. В частности, если в блок-схемах нет циклов, это еще не значит, что циклов нет в алгоритме. По существу, блок-схема это не язык, а средство для описания детерминизма.