Основные понятия про уравнения
Дано равенство f(x) = g(x), где f(x) и g(x) - алгебраические выражения, содержащие неизвестную величину х.
Требуется найти все значения х, которые удовлетворяют равенству (то есть значения х, подстановка которых равенство обращает его в верное числовое равенство). Равенство выступает в этом случае уравнением с одной неизвестной х. Множество значений х, при которых определены обе части уравнения, называют областью допустимых значений (ОДЗ) уравнения. Каждое значение х, удовлетворяющее уравнению, называется решением и корнем уравнения. Уравнение может и не иметь корней, тогда говорят, что множество его решений пусто. Решить уравнение - это значит найти все корни уравнения или доказать, что их нет.
Пример.
Уравнение 2 х + 1 = 5х – 2 имеет один корень.
Уравнение х 2 – х + 2 = 3х – 1 имеет два корня х = 1 и х = 3.
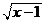Уравнение = -1 не имеет корней, множество его решений пусто Ø.
Два уравнения f1(x) = g1(x) и f2(x) = g2(x) называют равносильными (эквивалентными), если все корни одного уравнения одновременно являются корнями другого уравнения.
В процессе решения уравнений часто выполняют действия, в результате которых данное уравнение заменяется другим (обычно более простым), ему равносильным. Такой переход от одного уравнения другому может выполняться на основе следующих утверждений:
1) Если к обеим частям уравнения прибавить (вычесть) выражение, имеющее смысл во всей ОДЗ данного уравнения, то получите уравнение, равносильное данному.
Пример.
К обеим частям уравнения 2х + 1 = 5х – 2 прибавим выражение (-5х – 1). В результате получим уравнение, эквивалентное данному уравнению: 2х +1 = 5х – 2 Û -3х = -3
В частности, из этого утверждения вытекает правило о переносе членов уравнения из одной части в другую (с надлежащей переменой знака). Так, уравнение всегда можно записать в равносильной форме: f(x) – g(x) = 0.
Пример.
х2 – x + 2 = 3x – l Û x2– 4х + 3 = 0
2) Если обе части уравнения умножить (разделить) на выражение, не равное нулю и имеющее смысл во всей ОДЗ данного уравнения, то получится уравнение, равносильное данному.
Пример. Обе части уравнения -3х = -3 разделим на (-3). В результате получим уравнение, эквивалентное данному уравнению: -3х = -3 Û х = 1
7.2. Разновидности уравнений
Уравнения первой степени (линейные уравнения)
Уравнением первой степени (линейным уравнением) называют уравнение вида
ах + b = сх + d, где х - неизвестное, a, b, c, d - некоторые числа, причѐм, а ≠ с.
Для решения такого уравнения неизвестные слагаемые переносим в левую часть уравнения, а числа – в правую часть уравнения:
ax + b = cx + d Û (a – c)x = d – b
После этого левую и правую части уравнения делим на (а – с) ≠ 0. В результате
получим решение уравнения:
x = d - b
a - c
2. Уравнения второй степени (квадратные уравнения)
Корни квадратного уравнения
Уравнением второй степени (квадратным уравнением) называют уравнение вида ах2+ bх + с = 0, где х - неизвестная, а, b, с - некоторые числа, причѐм, а ≠ 0. В квадратном уравнении число а называют первым коэффициентом, число b - вторым коэффициентом, с – свободным членом.
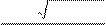Корни квадратного уравнения определяют по формуле:
x 1,2 =
- b ±
b 2 - 4 ac 2 a
Выражение D = b2 – 4ac называют дискриминантом квадратного уравнения.
Если D > 0, то уравнение имеет два действительных корня. Если D = 0, то уравнение имеет один действительный корень. Если D <0, то уравнение не имеет действительных корней.
Задание для самостоятельной работы.
1) Решить уравнения:
| 1. | х2 – 3x + 2 = 0 | 5. | 3х2 + 5х + 5 = х2 – 7х –7 |
| 2. | х2 + 2х – 8 = 0 | 6. | х2 + 6х + 7 = х2 – 3х + 2 |
| 3. | х2 + 7х = -10 | 7. | х2 + 5х – 10 = 3 – 5х – 2х2 |
| 4. | 3х2 – 8х + 1 = х – х2 – 1 |
2) Решить уравнения:
1. 2 = x +1
4. x -1 -4 - x =3
x x - 3 x + 2
2. 1 - 1 =1 5. 6 - x + x + 4 =-5
x + 2
x + 4 4
x + 2
1- x
|
x 2 + 2 x - 3 1
Частные случаи квадратных уравнений.
1) Уравнение вида х2 + рх + q = 0 называется приведенным квадратным уравнением. Данное уравнение можно получить из уравнения ах2 + bх + с = 0, если разделить его на а.
2) Уравнения вида ах2 + bх = 0 (с = 0) и ах2 + с = 0 (b = 0) называют неполными квадратными уравнениями.
Пример.
Как решить уравнения. 1) 3х2 + 5х = 0.
Разложим левую часть уравнения на множители:
3х2 + 5х = 0 Û х(3х + 5) = 0, следовательно х1 = 0, х2 = - 5
2) 4х2 – 25 = 0 Û 4х2 = 25, извлекая корень из левой и правой частей уравнения, получим: 2х = ±5, следовательно, х1 = 2,5 х2 = -2,5
Теорема Виета
Сумма корней приведенного квадратного уравнения x2 + px + q= 0 равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену: х1 + х2 = -р, х1:х2 = q.
Наоборот, если числа р, q, х1, х2 таковы, что х1 + х2 = -р, х1 –х2 = q, то х1, х2 - корни уравнения х2 + px + q = 0.
Пример.
Составить квадратное уравнение по его корням х1 = 3, х2 = -5. Определим р и q: p = -(3 – 5) = 2, q = 3·(-5) = -15.
Получим уравнение х2 + 2х – 15 = 0
Задание для самостоятельной работы.
Составить квадратные уравнения по их корням:
| 1. | х1 = 2, х2 = -4 | 3. | х1 = 5, х2 = -0,4 |
| 2. | х1 = -6, х2 = -7 | 4. | х1 = 3, х2 = 21 |
Квадратный трѐхчлен
Алгебраическое выражение ах2 + bх + с называют квадратным трѐхчленом. Если корни уравнения ах2 + bх + с = 0 равны х1 и х2, то квадратный трѐхчлен можно разложить на множители по формуле: ах2 + bх + с = а(х – х1)(х – х2).
Если корни уравнения ах2 + bх + с = 0 равны между собой, то есть х1= х2, то квадратный трѐхчлен можно разложить на множители по формуле:
ах2 + bх + с = а(х – х1)2
Пример.
Разложить на множители квадратный трѐхчлен 7x2 – 3х – 4
Корни уравнения 7х2 – 3х – 4 = 0 равны х1 = 1, х2 = - 4
Следовательно, 7х2 – 3х – 4 = 7 (х – 1)(х + 4)
Действие разложения квадратного трѐхчлена на множители используют при решении уравнений.
Пример.
Решить уравнение
2 x +1 +
x - 2
1- 3 x
x 2 + x - 6
= x +1
x + 3
Преобразуем знаменатель второго слагаемого:
2 x + 1 +
x - 2
1 - 3 x =
(x - 2)(x + 3)
x + 1
x + 3
После этого приводим выражение к общему знаменателю и получаем равносильное
x 2 + 5 x + 6
уравнение
(x - 2)(x + 3)
= 0.
Умножив обе части уравнения на выражение (x – 2)(x + 3),
приводим уравнение к виду
x 2 + 5 x + 6 = 0. Корнями уравнения является х1 = -2, х2 = -3.
Задание для самостоятельной работы.
1) Разложить множители на квадратные трѐхчлены:
| 1. | х2 + 2х – 8 = 0 | 3. | 3х2 – 2х – 5 = 0 |
| 2. | х2 + 7х + 10 = 0 | 4. | 4х2 – 7х – 15 = 0 |
2) 
Решить уравнения:
| 1. | x + 2 + x + 3 + x + 5 =0 x -1 x +1 1- x 2 |
| 2. | 2 x -1 + 3 x +1 = x -1 x + 2 x 2 - x - 6 x - 3 |
| 4. | 1 - 1 = 1 x 2 + x - 6 x 2 - x - 6 x 2 - 5 x + 6 |
| 5. | x -1 + x +1 +2(x + 4) =0 x + 2 x - 2 4 - x 2 |
Уравнения, которые приводятся к квадратным уравнениям
Уравнение вида ах4 + bх2+ с = 0 называется биквадратным уравнением. С помощью замены переменной по формуле х2 = y оно приводится к квадратному уравнению ay2 + by + с = 0.
Пример.
Решить уравнение х4 – 5х2 + 4 = 0. Выполним замену переменной х2 = у и получим уравнение у2 – 5у + 4 = 0. Корни данного уравнения равны у1 = 1, у2 = 4. Следовательно, х2 = 1, х2 = 4. Корни данных уравнений являются корнями исходного уравнения х1,2 = ±1, х3,4 = ±2.
Метод замены переменной применяется и в более сложных случаях. Пример.
Решить уравнение
x 2 +1 +
x
x
x 2 +1
= -2,5. Выполним замену переменной
x 2 + 1
|
x
В результате получим уравнение
y + 1 = -2,5, которое преобразуем к равносильному
y
квадратному уравнению у2 + 2,5у + 1 = 0. Корни данного уравнения равны у1 = -2, у2 = 0,5.
Подставив выражение
x 2 +1
x
, получим два уравнения
x 2 +1
x
= -2 и
x 2 +1
x
= -0,5, которые
приводятся к квадратным уравнениям х2 + 2х + 1 = 0 и х2 + 0,5х + 1 = 0. Первое уравнение имеет корень х = -1, второе уравнение корней не имеет. Следовательно, исходное уравнение имеет один корень х = -1.
Задание для самостоятельной работы.
Решить уравнения:
| 1. | х4 – 10х2 + 9 = 0 |
| 2. | 4х4 – 5х2 + 1 = 0 |
3. Иррациональные уравнения
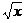
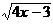Иррациональными называются уравнения, которые содержат неизвестную величину
под знаком корня. Например:
= 5,
= x. Во многих случаях, применяя возведение
в степень обеих частей уравнения, можно свести иррациональное уравнение к ал- гебраическому уравнению, которое является следствием исходного уравнения. Однако при возведении уравнения в степень могут полниться посторонние корни. Поэтому после решения алгебраического уравнения, к которому привели данное иррациональное уравнение, следует сделать проверку – подставить найденные корни в исходное уравнение и сохранить лишь те, которые ему удовлетворяют, а остальные – посторонние – отбросить.
Пример.
1) 
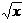= 5. Возводим в квадрат левую и правую части уравнения и находим корень
уравнения х = 5.
2) 
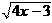= x. Возводим в квадрат левую и правую части уравнения
4х – 3 = х2 Û х2 – 4х + 3 = 0. Корни данного уравнения равны: х1 = 1, х2 = 3. Проверка показывает, что оба корня удовлетворяют исходному уравнению.
3) 
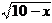= 3 x. Возводим в квадрат левую и правую части уравнения
10 – х = 9х2 Û 9х2 + х – 10 = 0. Корни данного уравнения равны х1 = 1, х2 = показывает, что исходному уравнению удовлетворяет только корень х1 = 1.
- 4. Проверка
7
Задание для самостоятельной работы.
Решить уравнения:
| 1. | 5 x - 6 = x | 8. | 2 x - 3 - x - 2 = 0 |
| 2. | 7 x - 8 = x | 9. | 2 x -1 + x + 4 = 6 |
| 3. | - 2 x = 5 x -1 | 10. | 10 - x - x + 3 = 1 |
| 4. | x +1 = 2 x | 11. | 2 x +1 + x - 8 = 7 |
| 5. | x + x + 4 = 3 x - 7 | 12. | x - 2 + 7 - x = 3 x |
| 6. | x 2 + 5 x + 1 + 1 - 2 x = 0 | 13. | x + 4 + 3 - 2 x = 1- 5 x |
| 7. | x -1 + x - 3 = 0 | 14. | x 2 + 2 x 2 - 5 = 13 |
7.3. 
Системы уравнений
Пусть даны равенства:
ì f 1 (x, y) =0,
|
|
где f1(x, y), f2(x, y) - алгебраические выражения, содержащие известные величины х и у. Требуется найти все значения х и у, которые одновременно удовлетворяют равенствам. Равенства называют системой двух уравнений с двумя неизвестными х и у. Значения х и у, удовлетворяющие уравнениям, называются решением системы уравнений. Решить систему уравнений - это значит найти все решения системы или доказать, что их нет.
Если система уравнений содержит п уравнений и п неизвестных, ее называют системой “п” уравнений с “п” неизвестными (число неизвестных может и не равняться числу уравнений).
Система называется совместной, если она имеет хотя бы одно решение, и
несовместной, если она не имеет ни одного решения.
Система называется определѐнной, если она имеет конечное число ращений, и
неопределѐнной, если она имеет бесконечное число решений.
Две системы называются равносильными, если они имеют одно и то же множество решений.
|
ì a 1 x + b 1 y = c 1,
называется системой двух линейных
|
уравнений (уравнений первого порядка) с двумя неизвестными.
Пример.
Решить системы уравнений.
|
î
Данную систему решим методом исключений (методом Гаусса). Для этого первое уравнение умножим на (–2) и сложим со вторым уравнением:
ì x +3 y =5, Ûì-2 x -6 y =-10,Ûì x +3 y =5,Ûì x +3 y =5,Ûì x =2,
|
|
|
|
|
|
î
Первое уравнение умножим на 2 и сложим со вторым уравнением:
ì 4 x - y =-6,Ûì8 x -2 y =-12,Ûì4 x - y =-6,
|
|
|
Данная система несовместная.
3) ì
5 x - 3 y = 2,
|
Первое уравнение умножим на 2 и сложим со вторым уравнением:
ì 5 x -3 y =2,
Ûì 10 x -6 y =4,
Ûì5 x -3 =2,
|
|
|
Данная система неопределѐнная.
í-10 x + 6 y = -4
í 0 = 0
Задание для самостоятельной работы.
Решить системы уравнений:
| 1. | ì2 x 1 -3 x 2 =8, x + 2 x = -3 î 1 2 | 7. | ì x -2 y =0, í x 2 + y 2 - 5 = 0 î |
| 2. | ì3 x 1 + x 2 =4, í6 x + 2 x = 1 î 1 2 | 8. | ì x 2 + y 2 + 3 xy = -1, í x + 2 y = 0 î |
| 3. | ì x 1 - x 2 =1, í2 x - 2 x = 2 î 1 2 | 9. | ì x 2 + xy - y 2 = 1, í x - 2 y = 1 î |
| 4. | ì 2 x 1 + x 2 +4 x 3 =8, ï x + x + x = 2, í 1 2 3 ïî- x 1 + x 2 - 2 x 3 = -2 | 10. | ì 3 x - y =5, í 2 2 î3 x - 2 xy - y - 7 = 0 |
| 5. | ì x 1+3 x 2 + x 3 =7, ï x + 2 x + x = 5, í 1 2 3 ïî x 1+ 3 x 2+ 5 x 3= 11 | 11. | ì x -5 y -3 =0, í2 2 î x - 3 xy - 2 y = 8 |
| 6. | ì - x 1 + x 2 + x 3 =8, ï2 x + x + x = 16, í 1 2 3 ïî3 x 2 + 4 x 3= 4 |