МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
РОССИЙСКОЙ ФЕДЕРАЦИИ
Государственное образовательное учреждение
Высшего профессионального образования
Санкт-Петербургского государственного университета
Сервиса и Экономики.
Контрольная работа
По дисциплине: Статистика.
Вариант №1.
Выполнила: Мельниченко Светлана
Вячеславовна
Студентка: 3 курса ИРЭиУ
Группы: 0605
Заочной формы обучения
Шифр специальности: 080109
Санкт-Петербург
Задача №1.
Приводятся данные по территориям Северного и Северо-Западного районов за 2002 год.
| Численность населения на 1.01. 2000, млн. чел. | Среднедушевой доход в месяц, тыс. руб. | Валовой региональный продукт, млрд. руб. | Численность (среднегодовая) занятых в экономике | Основные фонды в экономике (на конец года), млрд. руб. | |||
| Всего, млн. чел. | В % от численности населения | ||||||
| A | Z1 | Z2 | Z3 | Z4 | Z5 | Z6 | |
| Карелия | 0,8 | 1,7 | 11,3 | 0,312 | 40,8 | 81,3 | |
| Коми | 1,1 | 2,1 | 28,4 | 0,495 | 43,5 | 179,6 | |
| Архангельская | 1,5 | 1,2 | 22,8 | 0,567 | 38,9 | 170,5 | |
| Вологодская | 1,3 | 1,3 | 24,1 | 0,572 | 43,4 | 123,7 | |
| Мурманская | 1,0 | 2,5 | 23,8 | 0,423 | 42,3 | 142,1 | |
| СПб | 4,7 | 1,7 | 89,8 | 2,330 | 50,0 | 425,3 | |
| Ленинградская | 1,7 | 1,0 | 21,2 | 0,671 | 40,3 | 185,3 | |
| Новгородская | 0,7 | 1,4 | 9,4 | 0,303 | 41,7 | 61,1 | |
| Псковская | 0,8 | 0,9 | 6,5 | 0,302 | 37,7 | 69,1 |
Задание:
Необходимо построить групповую таблицу, выделив группы территорий со среднедушевым ежемесячным доходом: «до 1,500 тыс. руб.»; «1,500 тыс. руб. и более». В сказуемом рассчитать число территорий, в т.ч., в % к итогу, показатели обеспеченности ресурсами 1-ой территории, показатели доли занятых, фондовооружённости, фондоотдачи, выработки. Оформите таблицу с соблюдением известных правил. Проанализируйте результаты и основные выводы изложите в краткой аналитической записке.
|
|
Решение:
Построим таблицу:
| Группы территорий по ежемесячному доходу | Порядковый номер региона | Наименование области | Численность населения на l.01.2000, млн. чел. | Среднедушевой доход в месяц, тыс. руб. | Валовой региональный продукт, млрд. руб. | Численность (среднегодовая) занятых в экономике | Основные фонды в экономике (на конец года), млрд. руб. | Фондовооруженность, руб. | |
| Всего, млн. чел. | В % от численности населения | ||||||||
| А | |||||||||
| до 1500 руб. | Псковская | 0.8 | 0.9 | 6.5 | 0.302 | 37.7 | 69.1 | 228807.95 | |
| Ленинградская | 1.7 | 21.2 | 0.671 | 40.3 | 185.3 | 276154.99 | |||
| Архангельская | 1.5 | 1.2 | 22.8 | 0.567 | 38.9 | 170.5 | 300705.47 | ||
| Вологодская | 1.3 | 1.3 | 24.1 | 0.572 | 43.4 | 123.7 | 216258.74 | ||
| Новгородская | 0.7 | 1.4 | 9.4 | 0.303 | 41.7 | 61.1 | 201650.17 | ||
| Итого по группе | - | 2.415 | - | 609.7 | - | ||||
| в т.ч. в % к итогу | 55.56 | - | - | - | - | - | - | - | |
| В среднем по группе | 1.2 | 1.15 | 16.8 | 0.483 | 40.44 | 121.94 | 252463.77 | ||
| 1500 руб. и более | Карелия | 0.8 | 1.7 | 11.3 | 0.312 | 40.8 | 81.3 | 260576.92 | |
| СПб | 4.7 | 1.7 | 89.8 | 2.33 | 425.3 | 182532.19 | |||
| Коми | 1.1 | 2.1 | 28.4 | 0.495 | 43.5 | 179.6 | 362828.28 | ||
| Мурманская | 2.5 | 23.8 | 0.423 | 42.3 | 142.1 | 335933.81 | |||
| Итого по группе | 7.6 | - | 153.3 | 3.56 | - | 828.3 | - | ||
| в т.ч. в % к итогу | 44.44 | - | - | - | - | - | - | - | |
| В среднем по группе | 1.9 | 1.86 | 38.33 | 0.89 | 47.08 | 207.08 | 232668.54 | ||
| Всего по совокупности | 13.6 | 237.3 | 5.975 | - | |||||
| в т.ч. в % к итогу | - | - | - | - | - | - | |||
| В среднем по совокупности | 1.51 | 1.59 | 26.37 | 0.66 | 43.39 | 159.78 | 243665.89 |
Анализ полученной таблицы показывает, что в группе территорий по ежемесячному доходу «до 1500 тыс.руб.» 5 регионов, что составляет 55,56% от общего числа территорий. В среднем численность населения каждого региона в группе «до 1500 тыс.руб.» составляет 1,2 млн. чел., среднедушевой доход в группе составляет 1,15 тыс. руб. / мес., валовой региональный продукт составляет в среднем 16,8 млрд. руб.; в группе «до 1500 тыс.руб.» в среднем занято 40,44% населения от численности населения регионов, основные фонды в среднем составляют 121,94 млрд. руб. на регион, фондовооруженность составляет в среднем 252463.77 руб.
|
|
В группе территорий по ежемесячному доходу «1500 тыс.руб. и более» 4 региона, что составляет 44,44% от общего числа территорий. В среднем численность населения каждого региона в группе «1500 тыс.руб. и более» составляет 1,9 млн. чел., среднедушевой доход в группе составляет 1,86 тыс. руб. / мес., валовой региональный продукт составляет в среднем 38,33 млрд. руб.; в группе «1500 тыс.руб. и более» в среднем занято 47,08% населения от численности населения регионов, основные фонды в среднем составляют 207,08 млрд. руб. на регион, фондовооруженность составляет в среднем 232668.54 руб.
Необходимо отметить, что, несмотря на рост ежемесячного дохода как группировочного признака, средняя фондовооруженность в группе «1500 тыс.руб. и более» ниже, чем в группе «до 1500 тыс.руб.», однако в группе «1500 тыс.руб. и более» выше доля занятых в экономике, следовательно, можно сделать вывод о том, что уровень ежемесячного дохода в исследуемой совокупности не зависит только от фондовооруженности занятых, на уровень ежемесячного дохода влияют и другие факторы.
|
|
Задача №2.
Приводятся сведения по регионам Европейской части России.
Задание:
Выполните расчёт средних значений каждого показателя, укажите вид и форму использованных средних, приведите формулы расчёта, проверьте правильность результатов.
| Регионы | Численность населения, млн. чел. | Численность занятых в экономике в % от численности населения | Среднемесячная заработная плата 1-го занятого в экономике, тыс. руб. | Стоимость валового регионального продукта в среднем на | |
| 1-го занятого в экономике, тыс. руб. | 1 руб. стоимости основных фондов в экономике, коп. | ||||
| Л | П | К | В | Ф | |
| Северный | 5,7 | 41,7 | 2,06 | 46,6 | 15,8 |
| Северо-Западный | 7,9 | 45,9 | 1,69 | 35,2 | 17,1 |
| Центральный | 29,2 | 45,5 | 1,85 | 46,4 | 20,9 |
Решение:
Для расчета всех показателей используем формулу средней арифметической простой: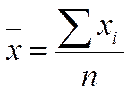 
| Регионы | Численность населения, млн. чел. | Численность занятых в экономике в % от численности населения | Среднемесячная заработная плата 1-го занятого в экономике, тыс. руб. | Стоимость валового регионального продукта в среднем на | |
| 1-го занятого в экономике, тыс. руб. | 1 руб. стоимости основных фондов в экономике, коп. | ||||
| Л | П | К | В | Ф | |
| Северный | 5.7 | 41.7 | 2.06 | 46.6 | 15.8 |
| Северо-Западный | 7.9 | 45.9 | 1.69 | 35.2 | 17.1 |
| Центральный | 29.2 | 45.5 | 1.85 | 46.4 | 20.9 |
| Средняя арифметическая простая | 14.27 | 44.37 | 1.867 | 42.733 | 17.933 |
Проверим полученные результаты, используя свойства средней – если средний показатель определен правильно, то сумма отклонений значений признака от среднего значения по совокупности должна быть равна нулю:
| Регионы | Расхождение между значением признака и средним значением | ||||
| Численность населения, млн. чел. | Численность занятых в экономике в % от численности населения | Среднемесячная заработная плата 1-го занятого в экономике, тыс. руб. | Стоимость валового регионального продукта в среднем на | ||
| 1-го занятого в экономике, тыс. руб. | 1 руб. стоимости основных фондов в экономике, коп. | ||||
| Л | П | К | В | Ф | |
| Северный | -8.57 | -2.67 | 0.193 | 3.867 | -2.133 |
| Северо-Западный | -6.37 | 1.53 | -0.177 | -7.533 | -0.833 |
| Центральный | 14.93 | 1.13 | -0.017 | 3.667 | 2.967 |
| Итого |
Анализ полученных результатов показывает, что вид используемых средних и сами средние значения показателей определены верно, т.к. при использовании других видов средних, например, при определении среднего значения показателя «Численность занятых в экономике в % от численности населения» как средней арифметической взвешенной нулевого значения суммы отклонений не получается.
Задача №3.
Приводятся данные за 2002 год о распределении территорий РФ по стоимости валового регионального продукта в среднем на 1 руб. стоимости основных фондов в экономике, копеек (E) -фондоотдача.
Задание: Выполните расчёт абсолютных и относительных показателей вариации (RE, 
, LE, 
), коэффициент асимметрии и показатель моды, постройте на одном графике гистограмму и полигон распределения частот; выполните анализ полученных результатов и оформите его в аналитической записке.
| Группы территорий РФ по стоимости валового регионального продукта в среднем на 1 руб. стоимости основных фондов в экономике (фондоотдача), копеек Ei | Число территорий в каждой группе, fi |
| от 7,6 до 11,3 | |
| от 11,3 до 15,0 | |
| от 15,0 до 18,7 | |
| от 18,7 до 22,4 | |
| от 22,4 и более | |
| Итого: |
Решение:
RE = 26.1 - 7.6 = 18,5 коп.
Составим вспомогательную таблицу:
| Интервалы | 
| 
| 
| Накопленные частоты |
| 7.6 - 11.3 | 9.45 | 160.65 | ||
| 11.3 - 15 | 13.15 | 433.95 | ||
| 15 - 18.7 | 16.85 | 235.9 | ||
| 18.7 - 22.4 | 20.55 | 205.5 | ||
| 22.4 - 26.1 | 24.25 | 72.75 | ||
| Итого | - | 1108.75 | - |
Среднюю арифметическую определим по формуле средней арифметической взвешенной:
| = 14.4 копеек |
Модальный интервал (с наибольшей частотой):2-й. Наибольшая частота: 33.
Моду определим по следующей формуле:
| = 12.99 копеек |
Построим вспомогательную таблицу:
| Интервалы |
|
|
| 
| 
| 
|
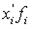
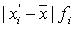
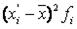
| 7.6 - 11.3 | 9.45 | 160.65 | 4.95 | 84.15 | 416.54 | |
| 11.3 - 15 | 13.15 | 433.95 | 1.25 | 41.25 | 51.56 | |
| 15 - 18.7 | 16.85 | 235.9 | 2.45 | 34.3 | 84.03 | |
| 18.7 - 22.4 | 20.55 | 205.5 | 6.15 | 61.5 | 378.22 | |
| 22.4 - 26.1 | 24.25 | 72.75 | 9.85 | 29.55 | 291.07 | |
| Итого | - | 1108.75 | 24.65 | 250.75 | 1221.42 |
Среднее линейное отклонение определим по следующей формуле:
| = | 3.26 |
Дисперсию определим по следующей формуле:
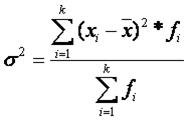
| = | 15.86 |
Среднее квадратическое отклонение определим по следующей формуле:
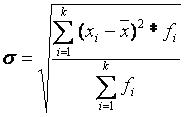
| = | 3.98 |
Коэффициент вариации определим по следующей формуле:
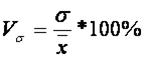
| = | 27.64 |
Для определения коэффициента асимметрии построим вспомогательную таблицу:
| Интервалы |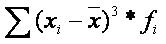 
| 
|
| 7.6 - 11.3 | -2061.89 | 10206.33 |
| 11.3 - 15 | -64.45 | 80.57 |
| 15 - 18.7 | 205.89 | 504.42 |
| 18.7 - 22.4 | 2326.08 | 14305.42 |
| 22.4 - 26.1 | 2867.01 | 28240.1 |
| Итого | 3272.64 | 53336.84 |
Коэффициент асимметрии определим по следующей формуле:
| = | 0.67 |
Гистограмма и полигон распределения частот:
|
По исследуемой совокупности размах вариации фондоотдачи составляет 18,5 коп.
Средняя фондоотдача в исследуемой совокупности составляет 14.4 копеек, при этом самым распространенным уровнем фондоотдачи является 12.99копеек.
Показатель среднего линейного отклонения говорит о том, что в данной совокупности фондоотдача в среднем отклоняется от своей средней величины на 3.26 копеек.
Показатель среднего квадратического отклонения говорит о том, что в данной совокупности фондоотдача в среднем отклоняется от своей средней величины на 3.98 копеек.
Значение коэффициента вариации указывает на однородность исследуемой совокупности.
Так как коэффициент асимметрии больше нуля, то распределение с правосторонней асимметрией.
Задача №4.
Структура среднего размера ежемесячных дотаций и льгот, полученных домашними хозяйствами (семьями) в 2000 году (на получателя в месяц, рублей).
Задание:
Проанализируйте особенности структур, используя оценочные показатели различий структуры.
| Дотации и льготы на: | Федеральные округа | |
| Центральный | Дальневосточный | |
| 1. питание | ||
| 2. оплату транспортных расходов | ||
| 3.оплату жилья и коммунальных услуг | ||
| 4. оплату отдыха | ||
| 5. оплату медицинских услуг | ||
| 6. содержание и обучение детей | ||
| 7. другие цели |
Решение:
| № п / п | Дотации и льготы на: | Федеральные округа | Отношение доли Дальневосточного к Центральному | |||
| Центральный | Дальневосточный | |||||
| руб. | % | руб. | % | |||
| Питание | 4.96 | 8.24 | 3.28 | |||
| Оплату транспортных расходов | 4.34 | 5.7 | 1.36 | |||
| Оплату жилья и коммунальных услуг | 3.4 | 5.79 | 2.39 | |||
| Оплату отдыха | 49.72 | 39.62 | -10.1 | |||
| Оплату медицинских услуг | 11.47 | 24.96 | 13.49 | |||
| Содержание и обучение детей | 23.11 | 10.12 | -12.99 | |||
| Другие цели | 3.01 | 5.57 | 2.56 | |||
| Итого | - |
Анализ полученных результатов показывает, что в структуре дотаций и льгот в Дальневосточном округе на 3,28 пункта выше доля дотаций на питание, на 1,36 пункта выше доля дотаций на оплату транспортных расходов, на 2,39 пункта выше доля дотаций и льгот на оплату жилья и коммунальных услуг, на 13,49 пункта выше доля дотаций на оплату медицинских услуг; на 2,56 пункта выше доля дотаций на другие цели, чем в Центральном округе. В структуре дотаций и льгот в Центральном округе выше доля дотаций и льгот на оплату отдыха, на содержание и обучение детей, чем в Дальневосточном округе.
Задача №5.
Имеются фактические данные государственной статистики о системе интернатных учреждений для детей.
| Виды интернатных учреждений для детей | Число учреждений | В них детей, тыс. человек | ||
| К0 | К1 | Д0 | Д1 | |
| Дома ребёнка | 18,5 | 19,3 | ||
| Детские дома | 42,4 | 72,3 | ||
| Детские дома-интернаты | 36,0 | 29,3 | ||
| Итого: | — | — | 96,9 | 120,9 |
Задание:
1.Определите недостающий признак-фактор и рассчитайте его отчётные и базисные значения.
2.Рассчитайте общие индексы: а) числа учреждений; б) численности детей в них в) индекс недостающего признака-фактора. Представьте результаты в системе взаимосвязанных индексов.
3.Определите абсолютный прирост численности детей в интернатных учреждениях за счёт каждого из двух факторов. Представьте результаты в виде взаимосвязанной системы.
Решение:
| Виды интернатных учреждений для детей | Число учреждений | В них детей, тыс. человек | Содержится в одном учреждении детей, чел. | |||
| Дома ребёнка | 18.5 | 19.3 | 69.81 | 75.98 | ||
| Детские дома | 42.4 | 72.3 | 75.18 | 58.12 | ||
| Детские дома-интернаты | 29.3 | 187.82 | ||||
| Итого: | 96.9 | 120.9 | - | - |
Общий индекс числа учреждений (Iу): 1.672
Общий индекс численности детей в учреждениях (Iч): 1.248
Общий индекс числа детей, содержащихся в одном учреждении (Iс): 1.34.
Система взаимосвязанных индексов: Iу = Iч* Iс => 1,672 = 1,248 * 1,34.
Анализ индексов показывает, что в целом за 1992 – 2002 г.г. число учреждений для детей выросло на 67,2%, при этом общее число детей, содержащихся в интернатных учреждениях, выросло на 24,8%, а число детей, содержащихся в среднем в каждом интернатном учреждении – на 34%.
Задача №6.
Проанализировать данные о реализации молочных продуктов в регионе.
| Группы молочных товаров | Выручка от реализации товаров, млн. руб. | Изменение цен за период, % | |
| База | Отчёт | 
| |
| W0 | W1 | ||
| Молоко | 490,9 | + 4 | |
| Сметана | 249,5 | + 8 | |
| Творог | 207,2 | + 11 | |
| Итого | 947,6 | ? |
Задание:
1.Рассчитайте индексы цен по каждой из трёх товарных групп.
2.Рассчитайте общий индекс цен как средний из индивидуальных индексов по схеме: а) Пааше; б) Ласпейреса;
3.Объясните причину различий их значений.
Решение:
Индекс цен по каждой товарной группе определим по формуле:
| Группы молочных товаров | Выручка от реализации товаров, млн. руб. | Индекс цен, ip | |
| База | Отчёт | ||
| W0 | W1 | ||
| Молоко | 490.9 | 1.04 | |
| Сметана | 249.5 | 1.08 | |
| Творог | 207.2 | 1.11 | |
| Итого | 947.6 | - |
Для расчета общего индекса цен по схемам паше и Ласпейреса построим вспомогательную таблицу:
| Группы молочных товаров | Выручка от реализации товаров, млн. руб. | p0q1 | iq | p1q0 | |
| База | Отчёт | ||||
| W0 | W1 | ||||
| Молоко | 490.9 | 472.02 | 1.18 | 416.02 | |
| Сметана | 249.5 | 231.02 | 1.1 | 226.82 | |
| Творог | 207.2 | 186.67 | 1.02 | 203.14 | |
| Итого | 947.6 | 889.71 | - | 845.98 |
а) по схеме Паше: Ip = 947.6 / 889.71 = 1.065;
б) по схеме Ласпейреса: Ip = 845.98 / 793 = 1.067.
Анализ полученных общих индексов цен показывает, что согласно схеме Пааше в среднем по трем товарным группам цены выросли в 1.065 раза или на 6,5%; согласно схеме Ласпейреса в среднем по трем товарным группам цены выросли в 1.067 раза или на 6,7%.
Индекс цен, определенный по схеме Ласпейреса, отличается от индекса цен, определенный по схеме Пааше, т.к. весами в индексе Ласпейреса выступает количество продукции базисного периода, а в индексе Пааше – отчетного периода.
Задача №7.
Приводятся данные государственной статистики о среднедушевых денежных доходах за месяц, тыс. руб. (Di), по территориям Российской Федерации за 2002 год.
Задание:
1.Проведите 13%-ую бесповторную выборку, используя таблицу случайных чисел.
2.Рассчитайте выборочную величину среднемесячного душевого дохода 
и долю территорий, где среднедушевой ежемесячный доход меньше среднедушевого прожиточного минимума населения за месяц во II полугодии 2002 года, который составил 1,26 тыс. руб. (
)
3.Определите среднюю возможную ошибку (μ) и с вероятностью 0,9722 предельную ошибку (Δ) для выборочной средней и для выборочной доли.
4.Рассчитайте доверительный интервал, в котором будут находиться генеральная средняя (
)и генеральная доля (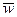
).
| № | Территория | Di | № | Территория | Di | № | Территория | Di |
| Белгородская обл. | 1,36 | Новгородская обл. | 1,71 | Саратовская обл. | 1,37 | |||
| Брянская обл. | 1,12 | Псковская обл. | 1,22 | Ульяновская обл. | 1,15 | |||
| Владимирская обл. | 1,09 | Респ. Адыгея | 1,11 | Курганская обл. | 1,19 | |||
| Воронежская обл. | 1,23 | Респ. Дагестан | 0,87 | Свердловская обл. | 1,68 | |||
| Ивановская обл. | 0,82 | Респ. Ингушетия | 0,52 | Тюменская обл. | 4,87 | |||
| Калужская обл. | 1,17 | Кабардино-Балкарская респ. | 1,12 | Челябинская обл. | 1,88 | |||
| Костромская обл. | 1,17 | Респ. Калмыкия | 0,93 | Респ. Алтай | 1,19 | |||
| Курская обл. | 1,27 | Карачаево-Черкесская респ. | 0,90 | Респ. Бурятия | 1,36 | |||
| Липецкая обл. | 1,69 | Респ. Северная Осетия-Алания | 1,84 | Респ. Тыва | 1,08 | |||
| Московская обл. | 1,86 | Краснодарский край | 1,55 | Респ. Хакасия | 1,53 | |||
| г. Москва | 8,53 | Ставропольский край | 1,34 | Алтайский край | 1,16 | |||
| Орловская обл. | 1,32 | Астраханская обл. | 1,46 | Красноярский край | 2,30 | |||
| Рязанская обл. | 1,11 | Волгоградская обл. | 1,17 | Иркутская обл. | 2,19 | |||
| Смоленская обл. | 1,65 | Ростовская обл. | 1,61 | Кемеровская обл. | 2,20 | |||
| Тамбовская обл. | 1,46 | Респ. Башкортостан | 1,69 | Новосибирская обл. | 1,31 | |||
| Тверская обл. | 1,20 | Респ. Марий Эл | 0,85 | Омская обл. | 1,27 | |||
| Тульская обл. | 1,41 | Респ. Мордовия | 1,12 | Томская обл. | 1,97 | |||
| Ярославская обл. | 1,65 | Респ. Татарстан | 1,75 | Читинская обл. | 0,96 | |||
| Респ. Карелия | 2,10 | Удмуртская респ. | 1,42 | Респ. Саха | 3,52 | |||
| Респ. Коми | 2,76 | Чувашская респ. | 0,99 | Приморский край | 1,61 | |||
| Архангельская обл. | 1,73 | Кировская обл. | 1,13 | Хабаровский край | 1,96 | |||
| Вологодская обл. | 1,75 | Нижегородская обл. | 1,39 | Амурская обл. | 1,50 | |||
| Калининградская обл. | 1,67 | Оренбургская обл. | 1,39 | Камчатская обл. | 2,93 | |||
| Ленинградская обл. | 1,32 | Пензенская обл. | 0,96 | Магаданская обл. | 2,93 | |||
| г. Санкт-Петербург | 2,41 | Пермская обл. | 2,14 | Сахалинская обл. | 2,53 | |||
| Мурманская обл. | 3,33 | Самарская обл. | 2,40 |
Решение:
Поскольку совокупность содержит 77 ед., то объем выборки составит 13% или 10 ед. Начальная точка: 16-я строка 5-й столбец. Получаем номера наблюдений для включения в выборку: 72, 58, 68, 03, 30, 06, 11, 44, 57, 18.
Определим выборочную величину среднемесячного душевого дохода:
| № | Территория | Доход |
| Приморский край | 1.61 | |
| Челябинская обл. | 1.88 | |
| Омская обл. | 1.27 | |
| Владимирская обл. | 1.09 | |
| Респ. Дагестан | 0.87 | |
| Калужская обл. | 1.17 | |
| г. Москва | 8.53 | |
| Респ. Татарстан | 1.75 | |
| Тюменская обл. | 4.87 | |
| Ярославская обл. | 1.65 |
Выборочная величина среднемесячного душевого дохода: = 2.47 тыс. руб.
Дисперсия: 5.817.
Среднее квадратическое отклонение: 2.41
Средняя ошибка выборки: 0.711
Предельная ошибка (t=2.2): 1.56
Границы генеральной средней: 0.91 ≤ xсред. ≤ 4.03
Таким образом, на основании проведенного выборочного обследования с вероятностью 0,9722 можно заключить, что среднемесячный душевой доход лежит в пределах от 0,91 до 4,03 тыс. руб.
Далее проведем анализ выборочной доли: w = 0.039
Дисперсия доли: 0.0375
Средняя ошибка выборки: 0.057
Предельная ошибка выборки (t=2.2): 0.1254
Границы генеральной доли: -0.0864 ≤ p ≤ 0.1644.
Следовательно, с вероятностью 0,9722 можно утверждать, что доля лиц, имеющих доход ниже 1,26 тыс. руб., не превышает 16.44%.
Задача №8.
Предлагается проанализировать фактические данные о численности специалистов, выпущенных высшими учебными заведениями РФ, тыс. чел., на начало учебного года
| Годы | |||||||||||
| Тыс. чел. | 406,8 | 425,3 | 443,6 | 409,9 | 403,2 | 428,2 | 457,7 | 500,8 | 554,8 | 635,1 | 720,0 |
Задание:
1.Определите вид динамического ряда и постройте график фактических уровней.
2.Рассчитайте показатели динамики за каждый год изучаемого отрезка времени.
3.Выполните расчёт динамических средних за I-ый период (1992-1995 гг.) и за II-ой период (1996-2002 гг.)
4.Проанализируйте результаты, сделайте выводы.
Решение:
Представленный в задаче динамический ряд интервальным рядом динамики с равноотстоящими уровнями. График фактических уровней:
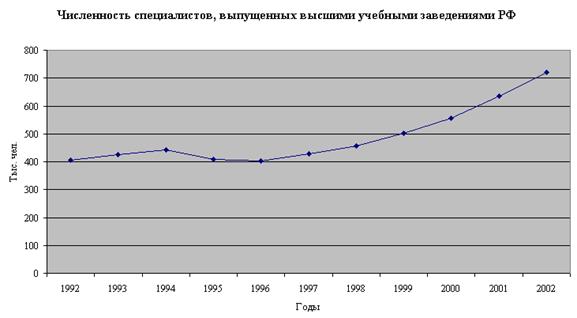
Определим показатели ряда динамики:
| Показатели | |||||||||||
| Абсолютный уровень ряда динамики | 406.8 | 425.3 | 443.6 | 409.9 | 403.2 | 428.2 | 457.7 | 500.8 | 554.8 | 635.1 | |
| Абсолютный прирост цепной | 18.5 | 18.3 | -33.7 | -6.7 | 29.5 | 43.1 | 54.0 | 80.3 | 84.9 | ||
| Абсолютный прирост базисный | 18.5 | 36.8 | 3.1 | -3.6 | 21.4 | 50.9 | 228.3 | 313.2 | |||
| Коэффициент роста цепной | 1.045 | 1.043 | 0.924 | 0.984 | 1.062 | 1.069 | 1.094 | 1.108 | 1.145 | 1.134 | |
| Коэффициент роста базисный | 1.045 | 1.09 | 1.008 | 0.991 | 1.053 | 1.125 | 1.231 | 1.364 | 1.561 | 1.77 | |
| Темп (процент) прироста | 4.548 | 4.303 | -7.597 | -1.635 | 6.2 | 6.889 | 9.417 | 10.783 | 14.474 | 13.368 | |
| Значение 1% прироста | 4.068 | 4.253 | 4.436 | 4.099 | 4.032 | 4.282 | 4.577 | 5.008 | 5.548 | 6.351 | |
| Средний уровень ряда | 489.582 | ||||||||||
| Средний абсолютный прирост | 31.32 | ||||||||||
| Средний коэффициент роста | 1.0588 | ||||||||||
| Средний темп прироста | 5.88 |
Далее выполним расчёт динамических средних за I-ый период (1992-1996 гг.) и за II-ой период (1997-2002 гг.).
| Период | Средняя |
| 1992-1996 г.г. | 417.76 |
| 1997-2002 гг. | 549.43 |
Анализ полученных результатов показывает, что за период исследования в среднем в год высшие учебные заведения выпускали 489.582 тыс. специалистов, при среднем ежегодном увеличении на 31,32 тыс. чел. или на 5,88%. Анализ динамических средних говорит о том, что в среднем во II-м периоде количество выпускников увеличилось на 131.67 тыс. чел., чем в I-м.