ЧАСТИЦА В ПОТЕНЦИАЛЬНОЙ ЯМЕ
Потенциальная яма — модель системы, в которой частицы могут удаляться от выделенной точки (центра) только на некоторое конечное расстояние. Физическая природа ограничений может быть различной. Так, например, система может быть окружена жесткими стенками, от которых частицы будут отражаться при столкновении; частицы могут быть связаны с центром жесткой или упругой связью и т.д. В любом случае на частицу действует возвращающая сила, заставляющая частицу совершать движения циклического типа в ограниченном объеме пространства.
Ясно, что структуры, наиболее интересные для химиков (атомы, ионы, молекулы) относятся к структурам именно такого типа, так как составляющие их частицы — ядра и электроны — движутся циклическим способом в ограниченном объеме пространства. Поэтому с помощью простой модели потенциальной ямы можно прояснить многие важные особенности атомов и молекул.
Модель "потенциальной ямы" отличается от модели "свободной частицы" тем, что в ней потенциальная энергия частицы отлична от нуля, по крайней мере, в некоторых областях пространства. С физической точки зрения, это означает, что в этих областях пространства на частицу действуют внешние силы, величина которых определяется зависимостью потенциальной энергии от пространственных координат: F = – grad U (x, y, z). Поскольку характер зависимости U от переменных x, y, z может быть весьма разнообразным, существует множество различных конкретных случаев. Среди них можно выделить некоторые стандартные ситуации:
- прямоугольная яма ("потенциальный ящик"),
- цилиндрическая яма ("жесткий плоский ротатор"),
- параболическая яма ("гармонический осциллятор") и др.
ЧАСТИЦА В ПОТЕНЦИАЛЬНОМ ЯЩИКЕ
В этом случае зависимость потенциальной энергии от пространственных координат имеет следующий вид (для простоты ограничимся одномерным случаем движения вдоль оси х):

В промежутке от х = 0 до х = L потенциальная энергия нулевая, и когда частица находится именно здесь (т.е. внутри "ящика"), на нее не действуют никакие силы. В остальных местах потенциальная энергия бесконечно велика, и поэтому частица не может выйти за пределы ящика: в момент касания стенки на частицу действует бесконечно большая сила, мгновенно обращающая направление ее движения. Другими словами, попав внутрь ящика частица уже не может выбраться за его пределы и вынуждена двигаться от стенки к стенке.
Классическое описание
В классической механике такой тип движения называется возвратно-поступательным: частица все время движется равномерно и прямолинейно (вдоль оси х), но направление движения периодически изменяется на противоположное. Следовательно, классическое описание такой частицы практически ничем не отличается от описания свободной частицы, за исключением некоторой потери определенности относительно направления движения. Все допустимые состояния частицы стационарны и каждое из них можно охарактеризовать двумя взаимосвязанными наблюдаемыми:
• энергия (Е = Т), имеющая определенное и постоянное значение, и всегда представляющей собой кинетическую энергию (за исключением точек возврата),
• импульс р и его проекция на ось х, который может иметь всего два возможных значения рх = ± р.
При этом выполняется соотношение Т = р 2/2 m.
В отличие от свободной частицы, для возвратно-поступательного движения можно определить еще одну наблюдаемую: частоту n = р /2 mL, имеющую смысл только для достаточно длинных промежутковвремени.
Подчеркнем то обстоятельство, что мы можем приготовить классическую частицу в состоянии с любой энергией (импульсом), и это состояние будет стационарным.
Отметим две особенности такой системы.
Во-первых, рассмотрим задачу о характере распределения частицы вдоль ящика. Если усреднить результаты наблюдений по достаточно большому промежутку времени, то мы получим полностью равномерное распределение. Действительно, так как частица всегда движется с одной и той же скоростью, то время, за которое она пробегает любой постоянный отрезок пути, будет одним и тем же, независимо от расположения этого отрезка внутри ящика (ближе к центру или к стенкам). Этот результат не зависит ни от величины энергии частицы, ни от размеров ящика..
Во-вторых, если сделать одну из стенок ящика подвижной и медленно (по сравнению с движением самой частицы) вдвигать ее в ящик, уменьшая тем самым его размер, то будет наблюдаться постепенное увеличение энергии частицы. Такой способ изменения энергии механической системы называется адиабатическим. Физический механизм этого явления достаточно понятен: когда частица отражается от неподвижной стенки, ее энергия не изменяется, но когда частица отражается от стенки, движущейся навстречу, она каждый раз приобретает небольшую дополнительную порцию энергии. Условие “медленности” обусловлено тем, что при быстром перемещении стенки частица может не успеть удариться об нее, и изменение размера системы произойдет без изменения энергии. Поэтому, в идеале, адиабатическим можно назвать только бесконечно медленное перемещение стенки. Подчеркнем, что процесс увеличения энергии связан с изменением пространственной координаты и, следовательно, с наличием механической силы (Fx = – dE / dx). Можно сказать, что частица, запертая в ящике, препятствует уменьшению его размера, и такое уменьшение всегда сопряжено с необходимостью преодоления силы сопротивления (давление) и совершенияработы, которая и идет на увеличение энергии частицы. Аналогично, если позволить подвижной стенке выдвигаться наружу, то частица сама будет совершать работу над внешней средой, и энергия частицы будет постепенно уменьшаться. С математической точки зрения этот процесс описывается с помощью понятия адиабатического инварианта (I): произведение импульса на размер ящика остается постоянной величиной р • L = I = const, тогда р = I / L и Т = I 2/2 mL 2.Другими словами, энергия зависит от размера ящика по квадратичному закону. Заметим, что при уменьшении размера ящика и увеличении скорости движения частицы, частота ее циклического движения будет возрастать вместе с энергией. При этом, отношение Т /n = I = const или Т = I n (энергия пропорциональна частоте). Это соотношение (в виде Е = h n) часто трактуется как чисто квантовомеханический закон. В действительности, такое соотношение обусловлено только адиабатическим характером воздействия на замкнутую механическую систему с циклическим типом движения.
Квантовомеханическое описание
В случае квантово-механической системы состояние движения частицы описывается вектором состояния или эквивалентной ему волновой функцией, зависящей от координаты х и от времени. Среди всех возможных состояний нас будут интересовать только некоторые выделенные состояния — стационарные. Для них волновая функция, как обычно, имеет стандартный вид:
j(x, t) = j(x) • e– i w t
а ее пространственная часть j(х) является решением стационарного уравнения Шредингера: Н j(х) = Е j(х). Оператор Гамильтона включает в себя только оператор кинетической энергии (потенциальная энергия во всей доступной области пространства равна 0) и уравнение Шредингера (в промежутке от 0 до L) имеет точно такой же вид, что и для свободной частицы. Общий вид решений получается в точности таким же, что и для свободной частицы:
j(х) = А j+ + В j– = А • ехр[ i(p /h) x ] + В • ехр[– i(p /h) x ].
Принципиальное отличие данного случая заключается в том, что в любой точке за пределами ящика волновая функция должна быть равна 0 (поскольку вероятность найти там частицу равна нулю). Это означает, что на вид возможных волновых функций (решений уравнения) накладываются ограничения (граничные условия):
j(х = 0) = 0 и j(х = L) = 0.
Подставим эти граничные значения координаты х в выражение для волновой функции и получим:
j(0) = А • ехр (0) + В • ехр (0) = А + В = 0
j(L) = А • ехр [ i(p /h) L ] + В • ехр [– i (p /h) L ] = 0.
Из первого уравнения следует, что В = – А. Сделаем эту подстановку во второе уравнение и получим:
j(L) = А {ехр [ i(p /h) L ] – ехр [–i(p /h) L ]} = 0.
Разность двух комплексно сопряженных чисел, которая стоит в фигурных скобках, можно преобразовать в соответствии с формулой Муавра (ехр [i • m ] = cos [ m ] + i • sin [ m ]):
j(L) = А {ехр [ i(p /h) L ] – ехр [–i(p /h) L ]} = А • 2i • sin [(p /h) L ] = 0.
Синус равен нулю тогда, когда угол кратен 180°. Следовательно, получаем условие (p /h) L = p • n, где n — любое целое число (n = 0, 1, 2,...).
Отсюда следует, что значения импульса и энергии, при которых возможен стационарный тип движения частицы в ящике, определяются формулами:
р = [(ph)/ L ] • n и Е = [(p2h2)/2 mL 2] • n 2 = R • n 2
Константа R может рассматриваться как некоторая единица энергии, величина которой приспособлена к конкретной модели с заданными значениями размера ящика (L) и массы запертой в нем частицы (m).
Таким образом, для микроскопической частицы в ящике стационарными являются не любые состояния, а только некоторые, выделенные в отношении значений импульса и энергии. Поскольку такие состояния образуют дискретное множество, их можно пронумеровать с помощью целого числа n, которое называется поступательным (или трансляционным) квантовым числом.
Полученные результаты можно изобразить графически в виде энергетической и импульсной диаграмм, которые состоят из дискретного множества энергетических или импульсных уровней.
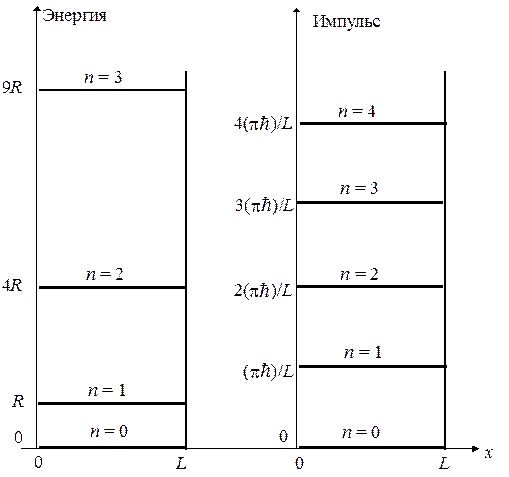
Уровни энергии образуют дискретный набор, расходящийся по квадратичному закону. Для характеристики подобных закономерностей часто используют понятие плотности уровней, которая равна числу уровней энергии, приходящихся на единичный интервал энергетической шкалы: W = dN / dE. Для рассматриваемого случая плотность уровней уменьшается по мере возрастания энергии по закону: W ~ 1/ E 2. Подчеркнем, что уровни энергии не вырождены, т.е. одному значению энергии отвечает одно состояние.
В связи с дискретным характером допустимых значений энергии, можно поставить такой вопрос: что произойдет, если приготовить частицу с начальной энергией, не совпадающей ни с одним из разрешенных значений? Такое начальное состояние будет нестационарным и с течением времени будет эволюционировать: в зависимости от внешнего окружения частица или потеряет или приобретет некоторое количество энергии. Эволюция закончится когда энергия частицы совпадет с одним из разрешенных значений.
Характер такой эволюции можно изобразить следующей схемой:

При любом начальном значении за малый промежуток времени (t *) энергия приобретет одно из стационарных значений и в дальнейшем будет оставаться постоянной. Механизм такой релаксации, обычно связан с электромагнитным взаимодействием между заряженной частицей и окружающей средой.
Поскольку время релаксации очень мало́ (для электронов t * ~ 10–8 с), то для больших промежутков времени можно вообще не принимать во внимание возможность короткоживущих нестационарных состояний и ограничиться рассмотрением только стационарных состояний. Именно такая ситуация имеет место в химии. Химические процессы сравнительно медленны, и поэтому короткоживущие нестационарные состояния атомов и молекул не оказывают на их протекание никакого влияния.
Обратимся теперь к анализу волновых функций, описывающих стационарные состояния. Мы выяснили, что они должны иметь вид:
j(х) = А • 2i • sin [(p /h) • х ] = А • 2i • sin [(p n / L) • x ].
Коэффициент А можно найти из условия нормировки: ò[j(х)]2 dx = 1.
Подставив выражение для функции, получим: 4 А 2òsin2[(p n / L) • x ] dx = 1. Табличный интеграл от квадрата синуса равен:
òsin2 (mx) dx = 1/2 х – (1/4 m) sin (2 mx)
Подставим пределы интегрирования (х = 0 и х = L) и получим:
4 А 2 òsin2 [(p n / L) • x ] dx = (4 А 2) [ L /2 – (L /4p n)sin(2p n)] = 1
или 4 А 2 (L /2) = A 2 (2 L) = 1, откуда найдем А = (1/2 L) 0,5.
Таким образом, окончательно получаем нормированный вид волновой функции:
j(х) = (2/ L) 0,5 • sin [(p n / L) • x ].
Заметим, что наличие или отсутствие множителя i (мнимой единицы) не играет никакой роли, так как при вычислении вероятностей (возведении в квадрат) он исчезает.
Теперь мы можем построить графические изображения самих волновых функций, а также их квадратов, которые задают пространственное распределение частицы по длине ящика.
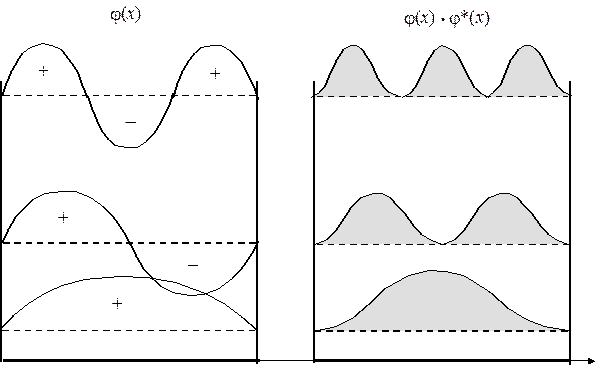
Отметим некоторые характерные особенности полученного результата.
Во-первых, волновая функция действительно имеет вид "волны". В определенных точках эта волна меняет свой знак на противоположный. Такие точки называются узловыми (или просто узлами). Каждой волновой функции можно приписать определенную узловую структуру — количество узлов и характер их распределения в пространстве. Такая структура изменяется закономерно по мере увеличения энергии или квантового числа. Это проявление общего квантовомеханического правила: чем больше узлов, тем выше энергия.
Поэтому знание только узловой структуры волновых функций позволяет распределить соответствующие состояния по энергетической шкале (т.е. построить качественную энергетическую диаграмму).
Во-вторых, пространственное распределение частицы не является равномерным, как в классическом описании. Напротив, имеются области, где вероятность обнаружения частицы больше, и, соответственно, меньше. При этом, наблюдается характерная зависимость функции распределения от величины энергии или квантового числа. Только при чрезвычайно больших значениях квантового числа: n → ∞ ("классический предел"), минимумы и максимумы располагаются так тесно, что не могут быть обнаружены экспериментально, и мы получаем усредненное "квазиравномерное" распределение.
В третьих при n = 0 и Е = 0 волновая функция повсюду обращается в 0. Это означает, что в таком состоянии частицу обнаружить невозможно, и, следовательно, такое состояние не является физически допустимым. Поэтому в качестве минимально возможного значения квантового числа необходимо принять n = 1, чему соответствует не равная нулю минимально допустимая величина энергии Е 1 = R. Эта энергия называется нулевой энергией, так как от нее отсчитывают, обычно, энергии всех прочих уровней. Подчеркнем, что наличие нулевой энергии является чисто квантовым эффектом.
Рассмотрим некоторые обобщения полученных результатов.
Влияние массы частицы
Масса частицы входит в выражение для энергии:
Е = [(p2h2)/2 mL 2] • n 2 = R • n 2,
из которого следует, что чем больше масса частицы, тем меньше будет величина постоянной R, и тем ближе друг к другу будет располагаться уровни энергии стационарных состояний. Другими словами, плотность уровней возрастает прямо пропорционально массе. При стремлении массы к бесконечности, т.е. в случае макроскопической частицы, плотность уровней также стремится к бесконечности. В этом случае дискретность практически исчезает и любое значение энергии становится допустимым, что полностью согласуется с предсказаниями классической механики.
Если рассмотреть серию частиц, например молекул, запертых в одинаковые ящики, то плотность уровней будет зависеть от массы этих молекул.
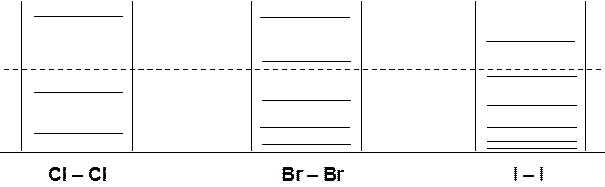
Из этой схемы легко видеть, что при заданных внешних условиях, определяющих некоторую максимально возможную энергию, разнообразие поступательных состояний тем больше, чем больше масса молекулы. В свою очередь разнообразие доступных состояний может оказывать заметное влияние на поведение молекул, в том числе и на их реакционную способность.
Влияние размеров ящика
Энергии стационарных состояний зависят от параметра L — длины нашего одномерного ящика, причем эта зависимость имеет обратно-квадратичный характер, точно такой же, что и в классическом случае. Разница заключается в том, что в квантовой механике не требуется соблюдение адиабатичности процедуры изменения размера ящика. Это связано с тем, что скорости движения микроскопических частиц настолько велики, что любые перемещения макроскопических стенок будут автоматически удовлетворять условию адиабатичности.
При уменьшении размеров ящика все уровни одновременно будут повышаться, причем квадратичный характер их относительного расположения сохранится. При очень малых размерах ящика можно получить ситуацию, когда разумной энергией будет обладать всего одно состояние (основное) и мы будем наблюдать систему, внутренняя энергия которой не поддается изменению ни при каких внешних воздействиях. Именно такая ситуация наблюдается для атомных ядер и элементарных частиц.
При увеличении размеров ящика, напротив, все уровни одновременно будут снижаться, причем квадратичный характер зависимости также сохранится. При увеличении размеров до бесконечности расстояния между соседними уровнями уменьшатся до нуля и дискретность уровней исчезнет, Мы получим еще один классический предел — любое значение энергии станет допустимым.
Отсюда вытекает важное заключение:
любые процессы, приводящие к изменению размеров доступной для связанной частицы области пространства, неизбежно сопряжены и с изменением энергии частицы.
Частица, предоставленная сама себе, будет стремиться заполнить собой весь доступный ей объем. Напротив, любые ограничения в доступном объеме требуют затраты внешней работы, т.е. могут протекать только в принудительном порядке, но не самопроизвольно.
Ясно, что чем меньше размер ящика, тем труднее его изменить, тем менее податливой к внешним воздействиям является система. Так, например, малые размеры атомов обуславливают высокую жесткость атомных структур и построенных из них веществ. Именно поэтому мы не проваливаемся сквозь пол, и в окружающем нас мире полно всяких жестких предметов. Здесь полезно провести аналогию с газом, запертым в сосуде: газ оказывает давление на стенки и сопротивляется попыткам уменьшения доступного ему объема. Аналогично, единственная микрочастица, запертая в микроскопическом объеме пространства, оказывает давление на стенки и сопротивляется попыткам уменьшения доступного ей объема. Различие только в характере зависимости давления от размеров ящика. Предоставленный самому себе газ стремиться занять как можно больший объем пространства. Аналогично, электрон, предоставленный самому себе, стремиться двигаться таким образом, чтобы ему был доступен наибольший возможный объем пространства.
Так, например, геометрическая форма молекул обусловлена тем, что электроны стремятся занять собой максимальный объем пространства. Поэтому деформировать молекулу можно только насильно, совершая над ней работу. При снятии внешних воздействий молекула самопроизвольно возвращается к равновесной форме, выделяя назад энергию, затраченную на ее деформацию.
При объединении электронных оболочек двух атомов объем пространства, доступный электронам, увеличивается, и энергия молекулы меньше энергии двух отдельных атомов. Разница составляет энергию химической связи. При попытках разделения молекулы на отдельные атомы мы ограничиваем область пространства, доступную для электронов, и должны совершать работу, идущую на разрушение химического взаимодействия.
Из полученной нами картины вытекает еще один вывод. Изменить энергию частицы, запертой в потенциальной яме, можно двумя принципиально различными способами.
Во-первых, мы можем изменить размер ящика, перемещая стенки. Характерно то, что при таком способе энергия частицы изменяется непрерывно и ей может быть придано любое значение. При таком процессе частица все время находится в стационарном квантовом состоянии, с одним и тем же значением квантового числа n. Работа, которую мы затрачиваем на увеличение энергии частицы, полностью сохраняется в системе и может быть всегда извлечена из нее назад в том же самом виде работы (для этого нужно совершить обратное перемещение стенки). Заметим, что таким способом у системы можно отнять даже нулевую энергию. Для этого, правда, придется увеличивать размер потенциального ящика до бесконечности.
Во-вторых, посредством некоторых возмущений (например, облучения или чрезвычайно резкого удара), при которых происходит кратковременный сдвиг стенки и возвращение ее в прежнее положение, частицу можно перевести в другое квантовое состояние. Естественно, что ее энергия при этом увеличится скачкообразно, "квантовым" образом. Размеры ящика в этом случае остаются прежними, и расположение энергетических уровней не меняется. Энергию, поглощенную частицей в таком квантовом скачке, нельзя полностью извлечь из системы в виде работы, а можно только в виде излучения с неопределенным направлением (хаотического).
Влияние формы ящика
Что произойдет, если стенки ящика сделать не вертикальными, а наклонными или кривыми? В качественном отношении картина не изменится, но численные значения энергий станут несколько другими.
Например, если сделать стенки расходящимися кверху, то очевидно, что по мере увеличения ширины ямы, степень расходимости уровней энергии будет становиться все меньше и меньше. Можно подобрать такую форму ямы, что уровни энергии вообще перестанут расходится, а будут расположены эквидистантно. Именно такая картина наблюдается для потенциальной ямы параболической формы (гармонический осциллятор). Если стенки ямы расширяются чересчур быстро, то уровни могут даже начать сходиться — расстояния между ними будут все меньше и меньше. Такая ситуация наблюдается для гиперболической ямы (кулоновские силы). В атоме водорода, например, энергетические уровни сходятся по квадратичному закону E = – R / n 2.
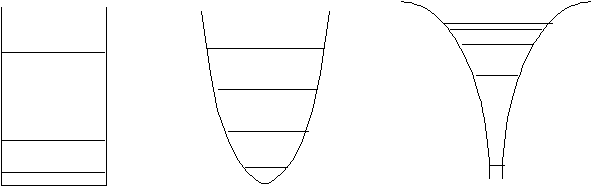
При изменении формы ямы изменяется и вид волновых функций. При этом, однако, узловая структура сохраняется полностью. Так, например, в атоме водорода 1 s -орбиталь не имеет узлов, 2 s -орбиталь имеет один узел и т.д. Другими словами, атомные орбитали представляют собой просто деформированные определенным образом отрезки синусоид, которые мы получили в качестве волновых функций частицы в ящике.