Уравнения математической физики
Классификация дифференциальных уравнений второго порядка в частных производных. Понятие корректности задачи для уравнений математической физики. Пример Адамара.
Некоторое выражение  является уравнением в частных производных.
является уравнением в частных производных.
Рассмотрим линейное ДУ 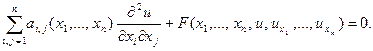 (1) Чтобы его упростить в точке
(1) Чтобы его упростить в точке  , мы должны в этой точке упростить соответствующую квадратичную форму
, мы должны в этой точке упростить соответствующую квадратичную форму  Из курса высшей алгебры известно, что любая квадратичная форма может быть приведена к каноническому виду
Из курса высшей алгебры известно, что любая квадратичная форма может быть приведена к каноническому виду  где
где  . Канонический вид формы зависит от коэффициентов
. Канонический вид формы зависит от коэффициентов  а значит и канонический вид (1) в фиксированной точке, также определяется
а значит и канонический вид (1) в фиксированной точке, также определяется 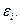 Если квадратичная форма знакоопределена, т. е. все
Если квадратичная форма знакоопределена, т. е. все  одного знака и отличны от нуля, то уравнение (1) относят к уравнениям эллиптического типа.
одного знака и отличны от нуля, то уравнение (1) относят к уравнениям эллиптического типа.
Если все  отличны от нуля и все за исключением одного имеют один знак, а этот один противоположного знака, то уравнение (1) относят к уравнением гиперболического типа. Если среди
отличны от нуля и все за исключением одного имеют один знак, а этот один противоположного знака, то уравнение (1) относят к уравнением гиперболического типа. Если среди  только один равен нулю, а все остальные одного знака, то тип уравнения – параболический. Если уравнение не относится ни к одному из перечисленных типов, то мы будем говорить, что уравнение не относится к УМФ. Может так оказаться, что тип уравнения в каждой точке одинаковый, то говорят, что тип уравнения одинаковый во всей области.
только один равен нулю, а все остальные одного знака, то тип уравнения – параболический. Если уравнение не относится ни к одному из перечисленных типов, то мы будем говорить, что уравнение не относится к УМФ. Может так оказаться, что тип уравнения в каждой точке одинаковый, то говорят, что тип уравнения одинаковый во всей области.
Уравнение вида  является уравнением гиперболического типа, т.е. уравнение описывающее колебание струны.
является уравнением гиперболического типа, т.е. уравнение описывающее колебание струны.
Уравнение вида  описывает процесс колебания струны, когда на неё действуют ещё какие-то силы.
описывает процесс колебания струны, когда на неё действуют ещё какие-то силы.
Уравнение колебания мембраны имеет вид 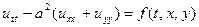 .
.
С помощью уравнений гиперболического типа описываются колебания.
Простейшее уравнение параболического типа - это уравнение теплопроводности 
Уравнение распространения тепла имеет вид  .
.

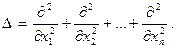
С помощью уравнения эллиптического типа описываются т.н. стационарные процессы, т.е. процессы независящие от времени. Простейший представитель уравнения эллиптического типа - это уравнение Лапласса 
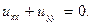
 ,т.е. задана задача Коши.
,т.е. задана задача Коши.
 , т.е. если концы струны закреплены, то задана смешанная задача.
, т.е. если концы струны закреплены, то задана смешанная задача.
Запись  обозначает, что на левом конце температура равна нулю,
обозначает, что на левом конце температура равна нулю,  -тепловой поток,
-тепловой поток,  ,
,  -температура окружающей
-температура окружающей
среды.
Задача для смешанного типа уравнений не ставится.
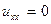 ,
, 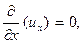 =>
=>  =>
=>  -это уравнение содержит две произвольные функции.
-это уравнение содержит две произвольные функции.
1) 
 ,Эта система составляет задачу Дирихле. 2)
,Эта система составляет задачу Дирихле. 2) 
 -вторая ограниченная задача или задача Нелли. 3)
-вторая ограниченная задача или задача Нелли. 3) 
 К сожалению, эту задачу мы решать не умеем.
К сожалению, эту задачу мы решать не умеем.
Корректно поставленная задача - это задача, которая имеет единственное решение и это решение должно быть устойчивым.
Пример Адамара -это пример некорректно поставленной задачи.
 -задача Коши для уравнения эллиптического вида.
-задача Коши для уравнения эллиптического вида.
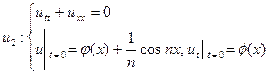 . Решение этих задач должно мало отличаться друг от друга.
. Решение этих задач должно мало отличаться друг от друга.  .
.  (1).Будем
(1).Будем
искать решение этой задачи в виде  Подставляя эту функцию в уравнение, получим
Подставляя эту функцию в уравнение, получим 
 .Если
.Если  ,то
,то

 Получаем, что функция
Получаем, что функция  удовлетворяет нашему уравнению, но она должна удовлетворять ещё начальным условиям.
удовлетворяет нашему уравнению, но она должна удовлетворять ещё начальным условиям. 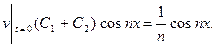 Отсюда следует, что
Отсюда следует, что  .
.  =>
=>  , получили систему
, получили систему  =>
=>  является решение задачи (1).
является решение задачи (1). 
Задачи Коши. Метод характеристик. Формула Даламбера.
Задача Коши для волнового ур-я: 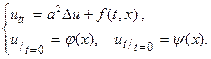
Задача Коши для ур-я теплопроводности: 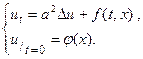
Метод характеристик.
Решим задачу, описывающую колебание струны (зад. Коши для однородн. волн. ур-я): 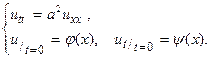 (1)
(1)
Найдём общее решение ур-я  (2), для этого приведём его к каноническому виду:
(2), для этого приведём его к каноническому виду:
Уравнение характеристик имеет вид dx=  dt (из ady=(b
dt (из ady=(b 
 )dx, где b=0, a=1, c=-a
)dx, где b=0, a=1, c=-a  , dy
, dy 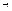 dx, dx
dx, dx 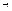 dt), характеристиками будут решения этого ур-я:
dt), характеристиками будут решения этого ур-я:
x-at=c  и x+at=c
и x+at=c  .
.
Сделаем замену ξ=x-at, η=x+at, и выразив производные  и
и  через ξ и η придём к уравнению
через ξ и η придём к уравнению  =0 (канонический вид ур-я (2)).
=0 (канонический вид ур-я (2)).
Общее решение этого ур-я u=F(ξ)+Φ(η).
Сделав обратную замену получим общее решение ур-я (2): U(t,x)=F(x-at)+Ф(x+at), где F и Ф – любые дифферинц. ф-ции. Подберём эти ф-ии так чтобы выполнялись начальные условия задачи (1).

Продифференцируем первое из ур-ий, умножим на a и сложим со вторым, получим:
2aФ’(x)=ψ(x)+aφ’(x)  Ф’(x)=
Ф’(x)=  , отсюда
, отсюда
Ф(x)= 

F(x)=φ(x)-ψ(x)= 
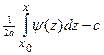 .
.
Тогда u(t,x)= 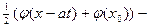
 +
+  +
+
 . Сократив и преобразовав, получим решение задачи (1):
. Сократив и преобразовав, получим решение задачи (1):
u(t,x)= 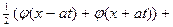
 - формула Даламбера
- формула Даламбера