Если количество уравнений равно количеству неизвестных, то система имеет единственное решение, если ранг системы меньше числа неизвестных, то количество решений бесконечно.
Обратный ход метода:
Если решение единственно:

Вопрос № 13: Однородная система линейных алгебраических уравнений:
1. Однородная система линейных алгебраических уравнений.
а) Свойства.
2. Теорема о существовании линейно независимых решений.
а) Доказательство.
Система называется однородной, если все свободные члены равны нулю.
Однородная система всегда совместна. Существует только одно решение.
Теоремииа о существовании не нулевых решений однородной системы:
Однородная система имеет не нулевые решения тогда, когда ранг матрицы коэффициентов меньше числа неизвестных.
Доказательство:
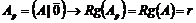
Не единственность решения 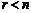
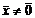
Однородная система с одинаковым количеством уравнений и неизвестных имеет не нулевые решения тогда, когда определитель матрицы коэффициентов не равен нулю.
Теорема:
Любая линейная комбинация решений однородной системы сама является её решением:
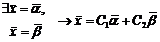
Доказательство:
Пусть существуют два решения, 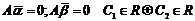
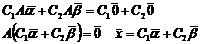
Теорема о существовании линейно независимых решений:
Путь ранг системы равен рангу матрицы коэффициентов и меньше числа неизвестных, тогда существует число линейно независимых решений, равное разности количества переменных и ранга системы.
Доказательство:
Пусть базисный минор содержится в левом верхнем углу матрицы.
Строки, не входящие в базисный минор можно отбросить, а свободные неизвестные перенести через знак равенства.
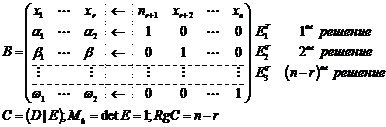
Вопрос № 14: Фундаментальная система решений однородной системы уравнений:
1. Фундаментальная система решений однородной системы уравнений.
2. Структура общего решения однородной и не однородной системы уравнений.
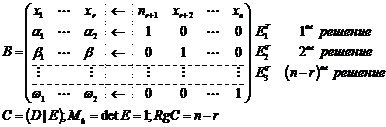
Структура общего решения однородной системы уравнений:
ФСР называется система из n-r линейно независимых частных решений
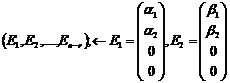
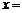
Теорема: Общее решение однородной системы уравнений:
Общим решением однородной системы линейных уравнений является линейная комбинация столбцов фундаментального решения.
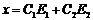
Структура общего решения не однородной системы уравнений:
Рассмотрим систему линейных уравнений: Неоднородная система 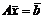 , однородная система:
, однородная система: 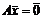
Теорема:
Разность двух решений неоднородной системы является решением соответствующей однородной системы.
Доказательство:
Пусть столбец α является решением неоднородной системы 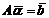 , β – решение системы
, β – решение системы 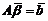 , тогда после вычитания одного из другого получим:
, тогда после вычитания одного из другого получим:  удовлетворяет однородной системе. Из теоремы следует, что общее решение однородной системы является суммой какого-либо её частного решения и общего решения соответствующей однородной системы
удовлетворяет однородной системе. Из теоремы следует, что общее решение однородной системы является суммой какого-либо её частного решения и общего решения соответствующей однородной системы


Вопрос № 15: Собственные векторы и собственные значения матрицы:
1. Собственные векторы матрицы.
2. Собственные значения матрицы.
а) Определение.
б) Свойства.
Арифметическим собственным вектором квадратной матрицы А порядка п называется такой не нулевой столбец:
 , где λ – собственной значение матрицы.
, где λ – собственной значение матрицы.
У каждой матрицы может быть пара из собственных векторов и собственных значений.
Множество всех собственных значений матрицы называется спектром.
 – ненулевые решения однородной системы уравнений.
– ненулевые решения однородной системы уравнений.
Однородная система имеет ненулевые решения, если ранг матрицы В равен количеству коэффициентов.
 – характеристическое уравнение матрицы А.
– характеристическое уравнение матрицы А.
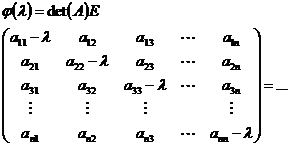 Проверить!!!¿¿¿
Проверить!!!¿¿¿
Рациональное алгебраическое уравнение степени N. Всегда имеет N корней, среди которых могут быть и кратные. Проверить!!!¿¿¿
Если определитель матрицы А равен нулю, то характеристический многочлен не содержит свободных членов.
У вырожденной матрицы хотя бы одно значение равно нулю. ¿¿¿
…???
При этом сами фундаментальные решения образуют систему линейно независимых уравнений.
Свойства собственных векторов и собственных значений матрицы:
1. Максимальное количество линейно независимых собственных векторов, соответствующих данному собственному значению 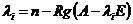 .
.
2. Линейная комбинация из собственных векторов соответствует одному и тому же, в свою очередь являющемуся собственным вектором для этого собственного значения.
3. Собственные векторы с попарно различными «чего-то такое???» значениями являются??? Проверить¿¿¿
4. Если матрица АТ=А, то все её собственные значения являются действительными числами.
5. Спектр вырожденной матрицы А содержит хотя бы один нулевой элемент.
6. Если матрица имеет пары??? комплексные сопряженные ¿¿¿,!!! То соответствующие им собственные векторы тоже комплексные.
Вопрос № 16: Нахождение собственных векторов и собственных значений матрицы:
Для вычисления собственных значений матрицы необходимо составить характеристическое уравнение: 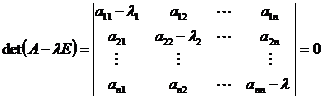
составив уравнение можно найти его корни, они-то и будут собственными значениями матрицы.
Собственные векторы матрицы соответствуют собственным значениям матрицы.
Вопрос № 17: Линейные операции над векторами:
1. Линейные операции над векторами.
2. Базис.
3. Координаты вектора.
4. Аффинная система координат.
а) На плоскости.
б) В пространстве.
5. Прямоугольная система координат.
а) На плоскости.
б) В пространстве.
Аналитическая геометрия – это методы решения геометрических задач с помощью аналитических операций.
Векторная алгебра:
D Геометрическим вектором называется направленный отрезок прямой, который можно переносить параллельно самому себе.
D Модулем вектора называется его длина.
D Нулевым вектором называется вектор, начало и конец которого совпадают.
D Коллинеарными называются вектора, лежащие на параллельных прямых.
D Равными называются коллинеарные, со направленные вектора, имеющие одинаковую длину.
D Компланорными называются векторы, расположенные в одной и той же, или в параллельных плоскостях.
Линейные операции над векторами:
1. Сложение:
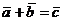
2. Умножение на число:

Вектор, умноженный на минус единицу меняет своё направление
на противоположенное.
3. Вычитание:
– это сложение с вектором, умноженным на минус единицу[3].
Теорема о взаимной колиниарности векторов:
Для всех векторов а, не равных нулю, все вектора в колиниарны а, то вектор в можно представить, как произведение вектора а на некоторое ненулевое число.
Свойства линейных операций над векторами:
1. 
2. 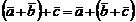
3. 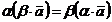
4. 
Линейная зависимость и независимость геометрических векторов:
Линейной комбинацией геометрических векторов  называется вектор
называется вектор 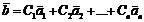
Системой из N векторов 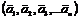 называется линейно независимой, если ни один из них не является и не может быть представлен в виде линейной комбинации других векторов этой системы.
называется линейно независимой, если ни один из них не является и не может быть представлен в виде линейной комбинации других векторов этой системы.
Если линейная комбинация всех этих векторов является нулевым вектором, то в случае равенства нулю всех «С»: 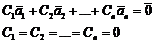 , иначе если “Ci” не равно нулю, то система векторов называется линейно зависимой.
, иначе если “Ci” не равно нулю, то система векторов называется линейно зависимой.
Теорема №1:
Два колиниарных вектора всегда линейно зависимы.
Теорема №2:
Три комплонарных[4] вектора всегда линейно зависимы.
Теорема №3:
Любые четыре геометрических вектора линейно зависимы.
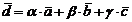
Базис:
Базисом на плоскости, или в пространстве называется максимальная система из линейно независимых векторов.
1. Базис на прямой является единственным вектором, параллельным данной прямой.
2. Базис на плоскости – это любая пара из не коллинеарных векторов, параллельных этой плоскости.
3. Базис в пространстве – это любые три не комплонарных вектора.
Разложение вектора по базису называется представление его в виде линейной комбинации векторов базиса.
Теорема:
Для заданного вектора а и выбранного базиса разложение, по базису является единственным.
Координаты вектора в базисе:
Координатами любого вектора в пространстве (в базисе) называются коэффициенты его разложения базису.
Свойства:
При сложении векторов одного и того же базиса, складываются соответствующие координаты.
При умножении вектора на число, умножаются все координаты этого вектора число.
Системы координат на плоскости и в пространстве:
Аффинная система координат:
Аффинной системой координат называется совокупность из точки – начала координат, и базиса.
Не аффинная система координат:
Не аффинной системой координат является полярная (цилиндрическая, сферическая) система координат.
Декартова система координат:
Частным случаем аффинной системы координат является прямоугольная Декартова система координат.
Вопрос № 18: Скалярное произведение векторов:
1. Скалярное произведение векторов.
а) Свойства.
б) Применение.
в) Выражение через координаты сомножителей.
Проекция вектора на вектор:

Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними.

Свойства:
1.  – Коммутативность.
– Коммутативность.
2. 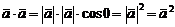
3. 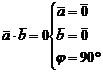
4. 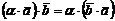
5. 

Скалярное произведение векторов, заданных своими декартовыми координатами равно сумме по парных произведений соответствующих координат сомножителей.
Применение скалярного произведения:
1. 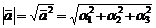
2. Определение перпендикулярности векторов, как скалярное произведение, равное нулю.
3. 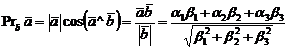
4. 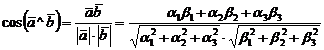
Вопрос № 19: Векторное произведение векторов:
1. Векторное произведение векторов.
а) Свойства.
б) Геометрический смысл.
в) Выражение через координаты сомножителей.
Векторным произведением векторов называется вектор, обозначаемый 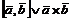 , который обладает двумя свойствами:
, который обладает двумя свойствами:
1. Перпендикулярен двум исходным векторам.
2. Составляет с исходными векторами правую тройку[5]
3. 
Направление результирующего вектора определяется по правилу буравчика.
Свойства векторного произведения:
1.  – проверка на колиниарности.
– проверка на колиниарности.
2. 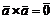
3. 
4. 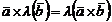
5. 
6. 
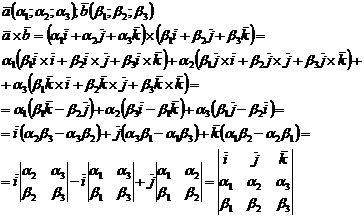
Вопрос № 20: Смешанное произведение векторов:
1. Смешанное произведение векторов.
а) Свойства.
б) Геометрический смысл.
в) Выражение через координаты сомножителей.
Смешанным произведением трёх векторов называется число, обозначаемое 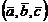 , равное скалярному произведению трёх его сомножителей, на векторное произведение двух первых.
, равное скалярному произведению трёх его сомножителей, на векторное произведение двух первых.
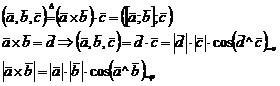
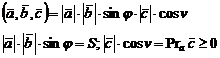
1.  >0, когда
>0, когда  , а значит угол v – острый, следовательно, вектора составляют правую тройку.
, а значит угол v – острый, следовательно, вектора составляют правую тройку.
2.  <0, когда
<0, когда 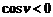 , а знаЭ
, а знаЭ
3. чит угол v – тупой, следовательно, вектора составляют левую тройку.
4. 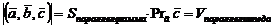
Свойства смешанного произведения:
1.  =0 тогда, когда
=0 тогда, когда  комплонарны.
комплонарны.
2. 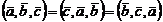
3. 
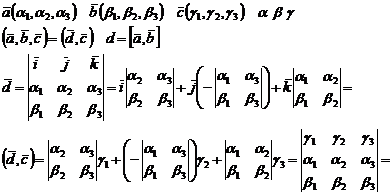
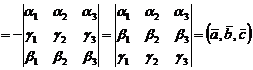
Вопрос № 21: Прямая на плоскости:
1. Прямая на плоскости.
а) Уравнения.
1) Общее.
2) Параметрическое.
3) Каноническое.
б) Расстояние до точки.
в) Угол между прямыми.
На плоскости задана прямоугольная декартова система координат.
Уравнение 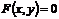 называется уравнением линии L на плоскости, если координаты всех точек линии подчиняются закону F, а координаты всех точек, не лежащих на линии
называется уравнением линии L на плоскости, если координаты всех точек линии подчиняются закону F, а координаты всех точек, не лежащих на линии 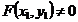 .
.
Линия – это геометрическое место точек, координаты которых удовлетворяют закону  – основное уравнение прямой на плоскости.
– основное уравнение прямой на плоскости.
Векторное уравнение прямой на плоскости:

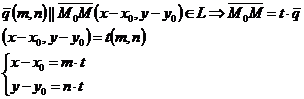
Параметрическое уравнение прямой на плоскости:

Каноническое уравнение прямой на плоскости:
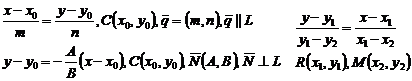
Расстояние от точки до прямой:

Угол между прямыми:
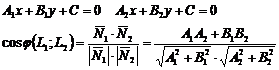
Вопрос № 22: Плоскость в пространстве:
1. Плоскость в пространстве.
а) Уравнение:
1) Общее.
2) Параметрическое.
3) Каноническое.
б) Расстояние до точки.
в) Угол между плоскостями.
Общее уравнение плоскости в пространстве:

Параметрическое уравнение прямой:
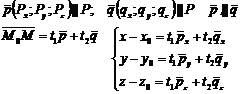
Векторное уравнение плоскости в пространстве:
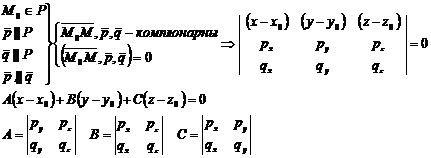
Расстояние от точки до плоскости:

Уравнение плоскости, проходящей через три заданные точки:
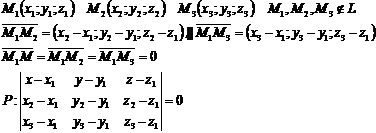
Угол между прямой и плоскостью:
Углом между прямой и плоскостью называется любой смежный угол, образованный самой прямой и проекцией этой прямой на плоскости:

Вопрос № 23: Прямая в пространстве:
1. Прямая в пространстве.
а) Уравнение.
1) Общее.
2) Параметрическое.
3) Каноническое.
4) Переходы между ними.
б) Угол между прямыми.
в) Угол между прямой и плоскостью.
Общее уравнение прямой в пространстве:
Общее уравнение прямой в пространстве выводится из условия задания прямой, как пересечения двух плоскостей:
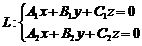
Параметрическое уравнение прямой:
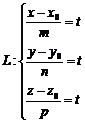
Каноническое уравнение прямой:
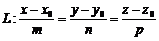
Угол между прямыми:
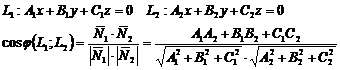
Угол между прямой и плоскостью:

Вопрос № 24: Три типа взаимного расположения прямых в пространстве:
1. Три типа расположения двух прямых в пространстве:
а) Параллельные прямые.
б) Пересекающиеся.
в) Скрещивающиеся прямые.
2. Расстояния:
а) Между точкой и прямой.
б) Между параллельными прямыми в пространстве.
в) Между скрещивающимися прямыми в пространстве.
Параллельные прямые в пространстве:
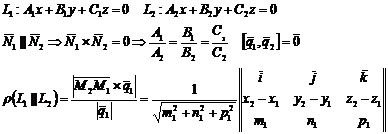
Пересекающиеся прямые в пространстве:

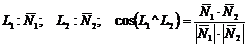
Скрещивающиеся прямые:
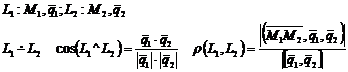
Вопрос № 25: Кривые второго порядка:
1. Кривые второго порядка.
а) Типы.
1) Геометрические определения
2) Канонические уравнения.
2. Общее уравнение.
а) Преобразование к каноническому.
1) Перенос начала координат.
2) Поворот осей.
Кривой второго порядка называется алгебраическая линия второй степени, общее уравнение которой имеет следующий вид: 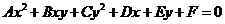 . Любые уравнения такого вида можно привести к каноническому виду.
. Любые уравнения такого вида можно привести к каноническому виду.
Кривые второго порядка подразделяются на Эллипс, Гиперболу и Параболу.
Эллипс:
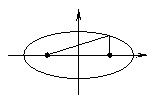 Эллипсом называется геометрическое место точек плоскости, сумма расстояний каждой из которых до двух заданных фокусов есть величина постоянная
Эллипсом называется геометрическое место точек плоскости, сумма расстояний каждой из которых до двух заданных фокусов есть величина постоянная
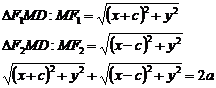

Эксцентриситет:
Эксцентриситет характеризует степень сжатия 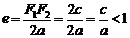
Коэффициент сжатия: 
Параметрическое уравнение эллипса:
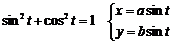
Оптические свойства:
Если взять эллиптическое зеркало, и в один из фокусов поместить источник света, то отражённые лучи пересекутся в другом фокусе.
Гипербола:
Гиперболой называется геометрическое место точек плоскости, абсолютная величина разности расстояний каждой из которых до двух заданных фокусов, находящихся на расстоянии 2с является величиной постоянной, равной 2а.
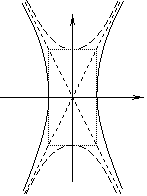
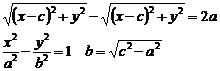
Эксцентриситет:
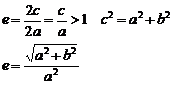
Оптические свойства:
Гиперболическое зеркало даёт расходящийся пучок света.
Парабола:
 Параболой называется геометрическое место точек плоскости, каждая из которых равноудалена от заданной точки – фокуса, и заданной прямой, называемой директрисой, причём расстояние от точки до прямой равно р:
Параболой называется геометрическое место точек плоскости, каждая из которых равноудалена от заданной точки – фокуса, и заданной прямой, называемой директрисой, причём расстояние от точки до прямой равно р:
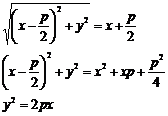
Приведение кривой к каноническому виду:
Приведение общего уравнения второго порядка к каноническому виду производится в два действия:
1. Определение новой системы координат, оси которой повёрнуты относительно основной. Поворот определяется слагаемыми, представляющими собой произведение переменных.
2. Сдвиг начала координат вдоль осей новой системы. Сдвиг определяется линейными членами уравнения. Преобразование на данной стадии осуществляется выделением полных квадратов.
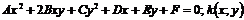 – квадратичная форма.
– квадратичная форма.
Приведение квадратичной формы к взвешенной сумме квадратов:
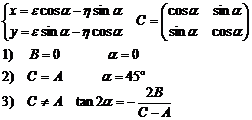 !!!¿¿¿
!!!¿¿¿
Вопрос № 26: Поверхности второго порядка:
1. Поверхности второго порядка.
а) Эллипсоид.
б) Конус.
в) Гиперболоиды.
2. Канонические уравнения.
3. Исследование форм методом сечений.
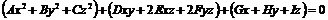
С помощью поворота можно исключить смежные произведения переменных, каждая их которых определяет свою поверхность (эллипсоид, гиперболоид, параболоид, конус, цилиндроид).
Исследование функции поверхности проводится при помощи канонического уравнения с помощью метода сечений.
Если все переменные в уравнении есть и все входят квадратично, то:
1. Если все слагаемые положительны, то 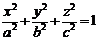 – Эллипсоид.
– Эллипсоид.
1)  Строим координаты сечения х=0
Строим координаты сечения х=0
(плоскость по YZ)
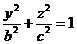
2) 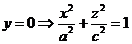
3) 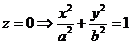
2.  – Однополосный гиперболоид.
– Однополосный гиперболоид.
1) 
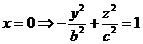
Гипербола:
2) 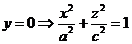
Эллипс:
3) 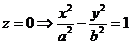
Парабола:

3.  – двух полосный гиперболоид:
– двух полосный гиперболоид:
1) 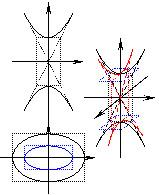

Гипербола:
2) 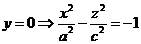
Гипербола:
3) 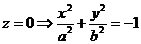
Эллипс:
4. 
 – Эллиптический конус
– Эллиптический конус
1) 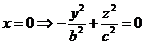
Пересекающиеся прямые:
2) 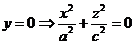
Эллипс:
3) 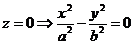
Пересекающиеся прямые:
Вопрос № 27: Поверхности второго порядка:
1. Поверхности второго порядка
а) Параболоиды.
б) Цилиндроиды.
2. Канонические уравнения.
3. Исследование форм методом сечений.
Все переменные есть, но две из них входят с квадратами, а одна линейно, получаемые таким образом поверхности называются параболоидами.
1. 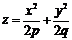 – эллиптический параболоид.
– эллиптический параболоид.
а)  – Парабола.
– Парабола.
б) 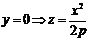 – Парабола.
– Парабола.
в) 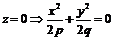 – Эллипс.
– Эллипс.
2.  – Гиперболический параболоид.
– Гиперболический параболоид.
а) 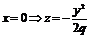 – Парабола, ветви вверх.
– Парабола, ветви вверх.
б) 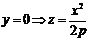 – Парабола, ветви вниз.
– Парабола, ветви вниз.
в) 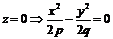 – Гипербола, симметрия относительно ОХ
– Гипербола, симметрия относительно ОХ
Цилиндроиды:
Отсутствует одна из переменных:
3. 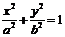 – Эллиптический цилиндр.
– Эллиптический цилиндр.
а) 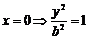 – две параллельные прямые.
– две параллельные прямые.
б) 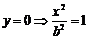 – две параллельные прямые.
– две параллельные прямые.
в) 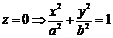 – Эллипс.
– Эллипс.
4. 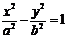
а)  – две параллельные прямые.
– две параллельные прямые.
б) 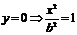 – две параллельные прямые.
– две параллельные прямые.
в) 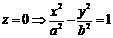 – Гипербола.
– Гипербола.
5.  – Параболический цилиндр.
– Параболический цилиндр.
Вопрос № 28: Квадратичная форма многих переменных и её матрица:
1. Квадратичная форма многих переменных.
а) Её матрицы.
2. Приведение квадратичной формы к каноническому виду.
а) Приведение квадратичной формы к взвешенной сумме квадратов.
Квадратичной формой N переменных называется однородный многочлен второй степени относительно этих переменных:
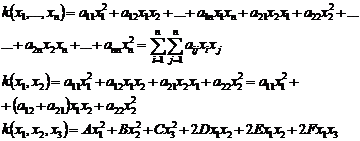
Квадратичную форму всегда можно представить в матричном виде:
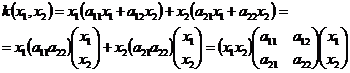
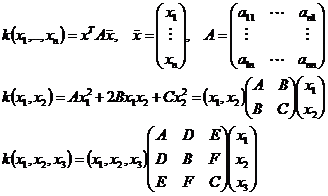
Диагональным, или каноническим видом квадратичной формы называют её вид в случае, если матрица коэффициентов является диагональной:

Для выполнения преобразования необходимо установить связь между исходными и новыми переменными
Линейное преобразование одной группы переменных:
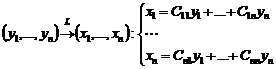 такое преобразование, при котором каждая из переменных х – линейная комбинация переменной у:
такое преобразование, при котором каждая из переменных х – линейная комбинация переменной у: 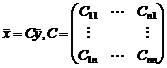
Если С не вырождена, то есть её определитель не равен нулю, существует обратная к ней матрица, такая, что:

Для приведения квадратичной формы к каноническому виду необходимо произвести такие преобразования, что бы матрица квадратичной формы стала диагональной.
Условия приведения квадратной матрицы к диагональному виду:
Если квадратная матрицы порядка п имеет несколько линейно независимых собственных векторов и соответствующих собственных значений, то она может быть приведена к диагональному виду, причём элементы диагональной матрицы являются собственные значения.
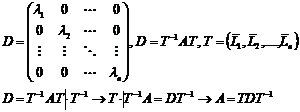
Пример:

Понятие об ортогонально матрице:
Для того, что бы новая, повёрнутая система координат была прямоугольной необходимо, что бы матрицы линейных преобразований была ортогональной.
Матрица линейных преобразований называется ортогональной, если её столбцы являются ортогональными арифметическими векторами.
Арифметическим вектором в линейной алгебре называется столбец из нескольких чисел
Скалярным произведением двух векторов одной и той же размерности называется сумма по парных произведений соответствующих координат. 
Нормой вектора называется квадратный корень из его скалярного квадрата.
Матрица С называется ортогональной, если её столбцы нормированы.
Ортогональная матрица обладает следующим свойством: операцию обращения можно заменить операцией транспонирования. 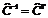
Процедура Шмидта ортогонализации матриц:
Любую систему линейно независимых векторов, то есть базис п -мерного пространства, можно преобразовать в ортогональную систему векторов с помощью следующей рекуррентной процедуры:

Любая арифметическая система координат может быть преобразована в прямоугольную систему координат:
Доказательство:

Применяя Процедуру Шмидта к столбцам невырожденной матрицы С можно сделать её ортогональной: 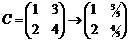
Приведение квадратичной формы к каноническому виду:

Для этого воспользуемся свойством собственных векторов и собственных значений матрицы А. Так как матрица А симметрична, все её собственные значения, среди которых могут быть кратные, являются действительными числами.
Каждому  кратности
кратности  соответствует
соответствует  штук собственных векторов (линейно независимых). Следовательно, полная система собственных векторов матрицы А состоит из п штук, и все они линейно независимы, по этому матрицу из квадратичной формы может быть преобразована к диагональному виду:
штук собственных векторов (линейно независимых). Следовательно, полная система собственных векторов матрицы А состоит из п штук, и все они линейно независимы, по этому матрицу из квадратичной формы может быть преобразована к диагональному виду:
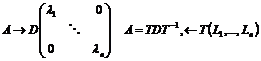
Так как все столбцы линейно независимой матрицы Т можно сделать ортогональными с помощью процедуры Шмидта, и нормированными, то:
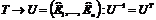
В результате матрицу квадратичной формы можно представить в виде: 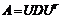 , тогда подставив это выражение в формулу квадратичной формы, получим:
, тогда подставив это выражение в формулу квадратичной формы, получим: 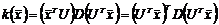
Замена 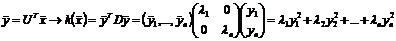
Любую квадратичную форму можно преобразовать с помощью линейного ортогонального преобразования в новые переменные, при этом старые и новые переменные будут связаны  , где U состоит из ортогональной и нормированной системы собственных векторов матрицы А квадратичной формы, при этом весовыми коэффициентами канонического представления являются собственный значения матрицы А.
, где U состоит из ортогональной и нормированной системы собственных векторов матрицы А квадратичной формы, при этом весовыми коэффициентами канонического представления являются собственный значения матрицы А.
Вопрос № 29: Знакоопределённые квадратичные формы многих переменных:
1. Знакоопределённые квадратичные формы многих переменных.
а) Критерии знакоопределенности.
1) Собственных значений.
2) Сильвестра.
Понятие знакоопределённости квадратичной формы используется для:
1. Определение типа кривой или поверхности второго порядка по её общему уравнению.
2. При исследовании функции многих переменных на экстремум, так как достаточным условием является знакоопределенность второго дифференциала.
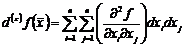
Квадратичная форма называется положительно определённой, если она при любых ненулевых значениях своих аргументов принимает только положительные значения.
Если квадратичная форма меньше, либо равна нулю, то она отрицательно полу определена, иначе не определена.
Критерии знакоопределённости квадратичной формы:
Критерий собственных значений матрицы:
Приведём квадратичную форму к каноническому виду:
 , тогда для всех х – у не равно нулю, так как квадрат не нулевых чисел больше нуля. Ответственность за знак квадратичной формы несу её коэффициенты.
, тогда для всех х – у не равно нулю, так как квадрат не нулевых чисел больше нуля. Ответственность за знак квадратичной формы несу её коэффициенты.
1. Если все собственные значения больше нуля, то квадратичная форма тоже больше нуля.
2. Если все собственные значения меньше нуля, то квадратичная форма тоже меньше нуля.
3. Если все собственные значения больше, либо равны нулю, то квадратичная форма тоже меньше нуля.
4. Если некоторые собственные значения равны нулю, а остальные меньше, то квадратичная форма отрицательно полу определена.
5. Если некоторые собственные значения больше нуля, а остальные меньше, то квадратичная форма может иметь любой знак.
Знакоопределённость квадратичной формы совпадает со знаками собственных значений её матрицы, то есть критерий собственных значений является полным, но трудоёмким, так как для вычисления собственных значений необходимо решить характеристическое уравнение матрицы.
Критерий Сильвестра:
Критерий Сильвестра позволяет выделить положительную и отрицательную знакоопределённость квадратичной формы с помощью вычисления нескольких определителей, являющихся угловыми минорами квадратичной формы.
После вычисления миноров суждение о знакоопределенности квадратичной формы выносится по следующему правилу:
1. Если все угловые миноры положительны, то квадратичная форма положительно определена.
2. Если угловые миноры чередуются знаком, начиная с минуса, то есть: 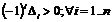 ,то квадратичная форма отрицательно определена.
,то квадратичная форма отрицательно определена.
3. Если идёт чередование знаков, начиная с плюса, или любое другое сочетание знаков, или существуют миноры, равные нулю (последний минор не равен нулю), то форма знака неопределенна.
4. Если последний минор равен нулю, в этом случае критерий Сильвестра не различает знакоопределённости формы, и необходимо использовать другой критерий.
Это свидетельствует о грубости метода.
Для заметок
[1] Для вычисления разности необходимо умножить вычитаемое на минус единицу и сложить получившиеся компоненты.
[2] Порядки матриц считаются согласованными, если число столбцов первой матрицы равно числу строк второй.
[3] Единичным называется такой вектор, который имеет единичную и колиниарен (параллелен) данному.
[4] Комплонарные вектора – вектора, лежащие в одной плоскости, или в параллельных плоскостях
[5] Тройка векторов называется правой, если из третьего вектора кротчайший поворот от первого ко второму виден, как поворот против часовой стрелки.