(7)
где а - коэффициент, определяемый при идентификации зависимости S(V).
Соответствующее значение nопт определяется по формуле
Так же, как и при вычислении nопт по формуле (3) в данном случае, при получении нецелочисленного значения nопт необходимо проверить неравенство (4) и установить nопт как это было описано выше. Далее, расчет осуществляется по формулам (5) и (6). Минимум общих издержек определяется по формуле
Кроме рассмотренных, также интересным для практики является случай, когда объем поставок, рассчитанный по формулам (5) и (7), не может быть реализован по причине ограниченной вместимости склада, либо из-за нехватки финансовых ресурсов, необходимых для оплаты поставки в определенный период времени, либо по каким-либо другим причинам. Иными словами, при определении оптимальной нормы запаса необходимо учитывать ограничение вида 
- предельный размер одной поставки. В этом случае целевая функция (1) примет вид
где l - неопределенный множитель, подлежащий определению.
Минимизация этой функции по V дает следующее значение для Vопт:
Порядок расчета оптимальных параметров управления с использованием этой формулы следующий. Вначале определяется значение Vопт для l=0. Если окажется, что 
, то дальнейшие вычисления осуществляются так, как это было описано выше. Если же будет иметь место неравенство 
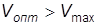, то значение оптимального объема поставок принимается равным 
, а дальнейшие вычисления оптимальных значений числа и периодичности поставок осуществляются аналогично рассмотренному ранее. Потери прибыли, которые возникают в связи с ограничением оптимального размера поставок, определяются следующим образом. Для случая постоянных удельных издержек по поставкам будем иметь потери прибыли, равные:
Аналогичным образом определяются потери прибыли для случая, когда имеет место скидка на размер поставки:
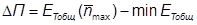
Значение DП является экономической оценкой ограничений на размер поставки. Исходя из этого значения, в каждом конкретном случае принимается решение о целесообразности элиминирования обстоятельств, порождающих указанные ограничения. Очевидно, что если стоимость устранения ограничения (например, аренда дополнительных складских площадей или заёма дополнительных финансовых ресурсов) оказывается выше величины DП, то с некоторой потерей прибыли стоит смириться. Если же имеет место обратное, то экономически целесообразно предпринять соответствующие действия, направленные на устранение обстоятельств, порождающих указанное ограничение.
Практическая часть.
Вариант №14
Исходные данные:
Общая потребность в ресурсе за интервал планирования -328 шт.,
Интервал планирования – 180 дней,
Удельные издержки хранения – 124 у.е./шт./интервал планирования,
Удельные издержки по поставкам (постоянная часть) – 18 у.е./поставку,
Коэффициент переменной части удельных издержек по поставкам:
а – 0,1 и а0 – 0,01,
Ограничения по максимальному размеру поставки – 30 шт.
В процессе расчёта в рамках модели управления ресурсами с постоянными удельными издержками по поставкам, а также для случая скидки на размер поставки определяем:
· оптимальный размер поставки;
шт.
· оптимальное число поставок;
поставок
т.к. результатом стало число не целочисленное в данном случае необходимо проверить неравенство следующего вида
где [nопт] – целая часть значения nопт
получаем
,
что не противоречит истине, следовательно, 
т.е.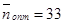 
поставки
Далее определяются объемы поставок по формуле:
шт.
При вычислении 
по этой формуле оказалось, что оптимальный объем измеряется дробным числом, в то время как по условию он должен быть целым. В этом случае необходимо в рамках 
организовывать некоторое количество поставок размером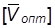 
и соответствующее число поставок размером 
так, чтобы в сумме 
число поставок удовлетворило потребность в размере Q. На данном примере мы можем это сделать вводя в расчёт 2-е переменные 
и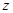 
и составляя простейшую систему уравнений
Корнями данного уравнения являются =31 и 
=2 т.е. для достижения 
=328 шт. в рамках 
=33 поставкам необходимо сделать 31 поставку по 10 шт. и 2-е поставки по 9шт.
· оптимальную периодичность поставок:
дней
· минимум величины суммарных издержек:
у.е.
Для случая скидки на размер поставки определяем оптимальный размер поставки;
· оптимальное число поставок;
шт.
· оптимальную периодичность поставок;
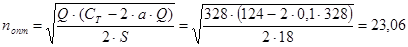поставок
т.к. объём поставки снова не целочисленное число делаем расчет подобный предыдущему пункту т.е. считаем неравенство
что противоречит истине, следовательно, = 24 поставкам. Далее определяем объёмы поставок по формуле:
шт.
определяем аналогично предыдущему пункту, а именно составляя систему уравнений
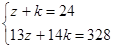
Корнями данного уравнения являются =16 и =8 т.е. для достижения 
=328 шт. в рамках =24 поставкам необходимо сделать 16 поставку по 14 шт. и 8 поставок по 13 шт.
· оптимальную периодичность поставок:
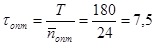дней
· минимум общих издержек по хранению и восполнению ресурсов;
у.е.
В процессе расчёта в рамках модели управления ресурсами с постоянными удельными издержками по поставкам и ограничением на поставку определяем:
шт.
Т.к. выполняется условие 
, то ограничения по поставке нет, следовательно, нет и потери по прибыли. Однако мы можем рассчитать потерю прибыли, когда имеет место скидка на размер поставки:
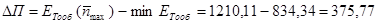у.е.
Для построения графиков сводим данные в таблицу
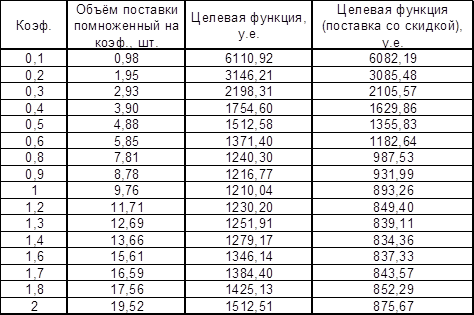
Аналитическая часть
На основе полученных результатов проводится анализ, в процессе которого сравниваем значения целевой функции при оптимальных значениях и значениях, отличающихся от оптимальных на 50% делается вывод о чувствительности соответствующей модели. В качестве примера выбираем модель управления ресурсами с применением скидки на размер поставки
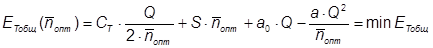
у.е.
у.е.
Разница составляет 82,98 у.е. или 9,9%, что по всей видимости говорит о нечувствительности системы к сильным изменения параметров управления