Лабораторная работа №4
«Применение одно продуктовых моделей управления ресурсами для управления процессом закупок и поставок на склад в условиях рынка».
Вариант № 14.
| Выполнил студент гр.4ВАП4 Молчанов Д.Н. Принял Диколов С.В. |
Москва 2003г.
Лабораторная работа №4.
Тема: применение одно продуктовых моделей управления ресурсами для управления процессом закупок и поставок на склад в условиях рынка.
Цель работы: является закрепление теоретического материала и приобретение практических навыков использования одно продуктовых моделей управления ресурсами в работе менеджеров по закупкам и поставкам ресурсов в условиях рынка.
Отчёт о проделанной работе.
Теоретическая часть.
Существует много моделей управления запасами, каждая из которых разработана для тех или иных производственно-технологических условий. Рассмотрим ряд наиболее простых моделей, относящихся к так называемым одно продуктовым, т.е. предназначенными для определения оптимальной нормы запаса одного вида ресурсов, поставляемых на склад и потребляемых со склада в течение некоторого цикла (планового периода) Т. Несмотря на свою простоту, эти модели нашли широкое применение в практике работы менеджеров, занимающихся материально-техническим обеспечением своей организации, т.к. оказались достаточно эффективными и не требующими больших затрат на вычисления.
Сначала рассмотрим ситуацию, когда потребление (спрос) ресурсов осуществляется с постоянной за цикл Т интенсивностью - m = const. Тогда общая потребность в ресурсе за один цикл составит величину 
. Ресурс восполняется за счет поставок объемом V, количество которых n выбирается таким образом, чтобы выполнялось условие 
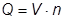. Обозначим также условные затраты по хранению ресурсов на складе СT, а удельные издержки по одной поставке, не связанные с объемом поставки величиной S. Общие затраты на хранение и поставку ресурсов на склад за время Т, зависящие от политики поставок, определяемой величинами n и V, составят
|
|
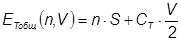
Если учесть взаимосвязь между n и V, то эти издержки можно записать так
(1)
Оптимальная норма запаса, т.е. величина 
будет иметь место тогда, когда ЕTобщ(V) будет минимальной. Таким образом, задача управления запасами в данной ситуации заключается в том, чтобы организовать процесс поставок объемом Vопт в количестве поставок, равном nопт, и периодичностью 
. Эти параметры можно определить, осуществляя минимизацию функции ЕTобщ. После определения первой производной и приравнивания ее к нулю, получим выражение
Отсюда определим оптимальный объем поставок
(2)
На основе выражения (2) определяем значение
(3)
При практическом использовании этой формулы необходимо учитывать, что в общем случае значения nопт могут получаться нецелочисленными, что противоречит физическому смыслу n как количества поставок. Округление по арифметическим правилам до целого в данном случае неправомерно, т.к. целевая функция ЕTобщ (n) несимметрична относительно значения nопт и указанная процедура округления может привести к существенной ошибке в определении минимума ЕTобщ. Для исключения возможной ошибки в данном случае необходимо проверить неравенство следующего вида
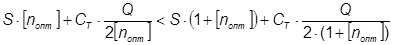(4)
где [nопт] – целая часть значения nопт
|
|
Если неравенство выполняется, то в качестве оптимального числа поставок принимается значение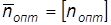 
. Если неравенство имеет противоположный смысл, то в качестве оптимального числа поставок принимается значение 
. Далее определяются объемы поставок по формуле:
(5)
При вычислении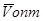 
по этой формуле может оказаться, что оптимальный объем измеряется дробным числом, в то время как по условию он должен быть целым. Например, когда ресурсы измеряются штуками (двигатели, запчасти и агрегаты, автомобили и т.п.). В этом случае необходимо в рамках 
организовывать некоторое количество поставок размером 
и соответствующее число поставок размером 
так, чтобы в сумме 
число поставок удовлетворило потребность в размере Q.
Оптимальная периодичность поставок определяется по формуле:
(6)
Расчет заканчивается определением минимума величины суммарных издержек по формуле:
В практике рыночных отношений встречаются ситуации, когда удельные затраты на поставку не являются постоянными как в рассмотренном выше случае, а зависят от размера поставок. Эта практика носит название скидок на размер поставок и осуществляется с целью заинтересовать потребителя в закупке оптовых поставок определенного размера, оптимального для производителя, т.к. производитель имеет возможность в этом случае существенно снизить свои затраты на производство, в частности, из-за уменьшения количества переналадок оборудования и смены технологической документации. Наиболее часто в указанных ситуациях зависимость удельных затрат на поставку выражается следующим образом
|
|
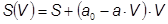
где S - часть издержек на поставку, не зависящая от ее объема,
- дополнительные расходы, зависящие от объема поставок.
С учетом этого обстоятельства, суммарные издержки на хранение и поставки (целевая функция) будут равны
Учитывая взаимосвязь n и V при условии m=const, целевую функцию можно представить в следующем виде
