Министерство науки и высшего образования
Российской Федерации
Федеральное государственное бюджетное образовательное учреждение
Высшего образования
«Московский государственный технологический университет «СТАНКИН»
(ФГБОУ ВО «МГТУ «СТАНКИН»)
Институт автоматизации и робототехники
Кафедра робототехники и мехатроники
Дисциплина «Пакет прикладных программ Matlab для исследований и разработок»
ОТЧЁТ
По лабораторной работе
на тему:
«Основы программирования в среде MATLAB/Scilab»
Выполнил:
студент группы АДБ-18-09 __________ _______ Сулаев Т.А.
(дата) (подпись) (ФИО)
Принял
преподаватель: __________ _______ Ким В. Л.
(дата) (подпись) (ФИО)
Оценка: ________ Дата:_________
Москва 2020
Цель работы: получение базовых знаний для работы в среде MATLAB: создание векторов и матриц, проведение основных операций с ними, знакомство со встроенными функциями среды.
Задание №1:
Вычислите выражение, заданное в таблице 1 согласно вашему варианту. В качестве переменной N можно выбрать любое положительное число (желательно не слишком большое).
Решение:
N=9
N =
9.
--> A=cos(N)^2
A =
0.8301584
--> B=log10(N^2)*log2(N^4 + N^2)
B =
24.232802
C=exp(N - 1)
C =
2980.9580
--> D=A - 2*B
D =
-47.635445
--> ans=(A^2\9 - B^1\2)\(C^2 + D + A^2 + B^5)^2
ans =
2.291D+13
1.1. попробуйте незначительно изменить исходное выражение, заданное в
таблице согласно вашему варианту (например, поменять знак сложения на знак
вычитания) и пересчитать, не вводя заново выражение, а воспользоваться тем,
что система запоминает все последние действия пользователя (для это нужно
использовать клавишу ↑).
A=cos(N)^3
A =
-0.7563824
ans =
1.900D+13
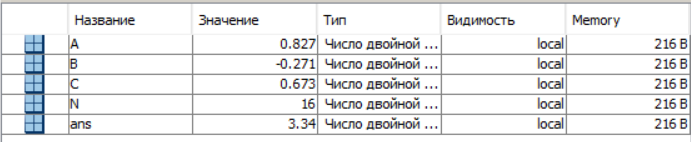
Задание 1.2: Получите результаты вычислений пункта 1.1. в форматах short и long
Операция short
y = iconvert(A, 2)
y =
--> y = iconvert(B, 2)
y =
--> y = iconvert(C, 2)
y =
--> y = iconvert(D, 2)
y =
-47
--> y = iconvert((A^2\9 - B^1\2)\(C^2 + D + A^2 + B^5)^2, 2)
y =
0
Операция long
y = iconvert(A, 4)
y =
--> y = iconvert(B, 4)
y =
--> y = iconvert(C, 4)
y =
--> y = iconvert(D, 4)
y =
-47
--> y = iconvert((A^2\9 - B^1\2)\(C^2 + D + A^2 + B^5)^2, 4)
y =
-2147483648
Задание №2: операции с матрицами и комплексными числами.
2.1 Получите комплексное число a+ bi, где a и b, - любые действительные числа. Определите:
- комплексно-сопряженное число числу a +bi;
- вычислите квадрат комплексно-сопряженного числа;
- вычислите произведение исходного комплексного числа и комплексносопряженного числа;
- вычислите выражение. sin(a+ bi) + cos(a +bi)
--> a= 13; --> A=a+b*%i A = 13. + 99.i
--> b=99; --> B=a-b*%i B = 13. - 99.i
--> A*B ans = 9970. + 0.i
-->sin(a+b*%i)+cos(a+b*%i) ans = 6.564D+42 + 2.409D+42i
2.2 Введите две матрицы A и B размерностью три на три (используйте любые действительные числа для заполнения матриц).
| B 2 8 7 6 1 4 5 2 1 |
| A 3 2 3 2 7 6 7 8 1 |
Задаём значение в матрицы.
A=[3 2 3; 2 7 6; 7 8 1] B=[2 8 7; 6 1 4; 5 2 1 ]
2.3 Выполнение над матрицами операций сложения, вычитания, умножения и деления.
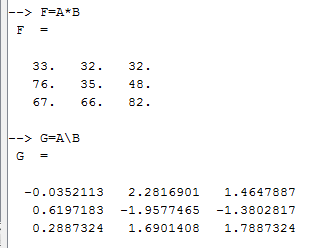
2.4 Выполните транспонирование матриц A и B
2.5 Создание матрицы С с комплексными числами.
| --> C=A+B 1. + 9.i 4. + 6.i 7. + 3.i 2. + 8.i 5. + 5.i 8. + 2.i 3. + 7.i 6. + 4.i 9. + i |
| --> B=B*%i 0. + 9.i 0. + 6.i 0. + 3.i 0. + 8.i 0. + 5.i 0. + 2.i 0. + 7.i 0. + 4.i 0. + i |
2.6 Матрица G комплексно сопряжённая матрице С
| --> G = C’ 30 - 2*i 84 - 6*5i 138 - 11*i 24 + 0*i 69 + 0*i 114 + 0*i 18 - 4*i 54 - 8*5i 90 - 13*i |
2.7 Возведение матрицы А в квадрат двумя способами.
.
2.8 Вычисление произведения первой строки матрицы A,и матрицы B, а также произведение матрицы B и третьего столбца матрицы A.
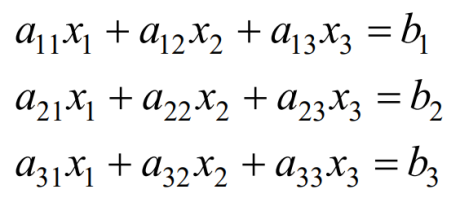
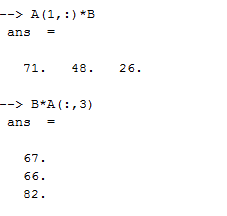
2.9 Решнние системы линейных уравнений.
-->B1=[-1.32; -3.91; -5.4]
-->x_inv=inv(A1)*-B1
2.10 Создание блочной матрицы К из транспонированных матриц А и В.
2.11 Удаление второго столбца и третьеё строки из матрицы К.
2.12 Заполнение матрицы нулями и заполнение необходимой области 5.
| --> k =eye(5,5) 1 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 1 |
| --> K =eye(7,4) 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 |
| --> o=ones(9,9) 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 |
Прямоугольная и квадратная матрица состоящая из единиц
| --> O=ones(6,4) 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 |
2.15 Создайте с помощью функции rand матрицу 4 на 5, элементы которой представляют собой случайные числа в интервале от 0 до N, где N - номер вашего варианта.
| G =16*rand(4,5) G = 3.3811978 10.646098 14.051464 11.621611 3.6995795 12.096702 10.054269 1.0939846 3.1762301 3.4634122 0.0035382 13.595924 8.9735777 8.7081171 14.134221 5.2852335 10.971696 10.597711 3.7131966 10.440216 |
2.16
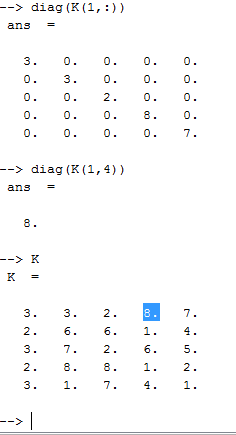
Из элементов первой строки блочной матрицы К с помощью функции diag сформируйте диагональную матрицу.
| g=B/A -0.049 1.197 -0.035 2.380 -0.521 -0.014 1.113 -0.451 0.366 |
| l=B*A 33. 32. 32. 76. 35. 48. 67. 66. 82. |
| G=A\B -0.035 2.282 1.465 0.619 -1.958 -1.380 0.289 1.690 1.789 |
| L=A*B 33. 32. 32. 76. 35. 48. 67. 66. 82. |
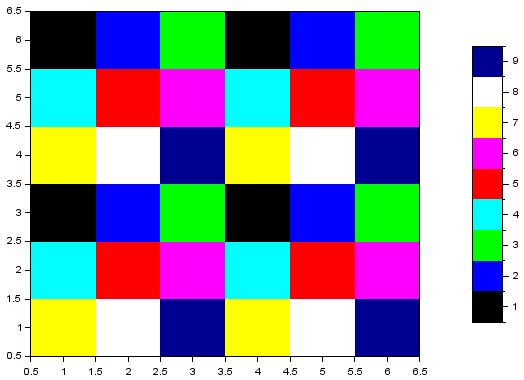
2.18 Выполните визуализацию блочной матрицы, используя команды Matplot, colorbar, colormap(gray). Объясните, какой результат позволяет получить каждая из команд.
-->Matplot(t)
-->colorbar
-->foo=scf();Matplot(T)
-->colorbar
-->foo.color_map=graycolormap(32)
| --> T=[A,A; A,A] 1 2 3 1 2 3 4 5 6 4 5 6 7 8 9 7 8 9 1 2 3 1 2 3 4 5 6 4 5 6 7 8 9 7 8 9 |
| Визуализация блочной матрицы |
Matplot() ‒ это лист иерархии графических объектов. Он представляет двумерные графики поверхности, используя цвета и изображения.
Сolorbar() ‒ рисует вертикальную цветную полосу справа от текущих осей. Ширина намеченных осей предварительно сужается на 15%. Освобожденная комната используется для цветной полосы, которая состоит из своих собственных осей.
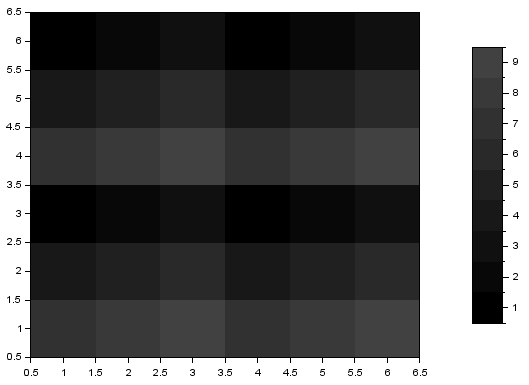
Сolormap(gray)‒ Команда устанавливает палитру затемнённости.
| Визуализация блочной матрицы с градацией серого |
| R 0.7071068 -0.7071068 0 0.7071068 0.7071068 0 0 0 1 |
| --> A4=[1,0,-1;1,0,1;0,1,0] 1 0 -1 1 0 1 0 1 0 |
-->det(A4) ans = -2
--> R=[sqrt(2)/2, -sqrt(2)/2, 0; sqrt(2)/2, sqrt(2)/2, 0; 0, 0, 1]
-->det(R) ans = 1.0000000
2.20 Определение ранга матрицы.
| D 1 0 0 0 0 1 0 1 0 0 0 0 0 1 0 0 |
-->D=[1,0,0,0;0,1,0,1;0,0,0,0;0,1,0,0]
-->rank(D) ans = 3
2.21 Скалярное произведение двух векторов
По Dot не получилось 
| -->cross(a,b) -4 -1 |
| --> b=[2;1;-1] -1 |
| --> a=[1;1;3] |
Задание №3: применение функций и команд MATLAB для выполнения инженерных расчётов.
3.1 Определить 1 v и удостовериться, что величина скорости движущегося объекта будет одинаковой для обоих наблюдателей, т.е. 1 v.=2v
| X -2 -4 |
| V2 |
| V1 0. -1. 0. 1. 0. 0. 0. 0. 1. |
-->V1=[cosd(f), -sind(f), 0; sind(f), cosd(f), 0; 0, 0, 1]
-->V2=[1;2;4]
-->x=linsolve(V1,V2)
-->v1=sqrt(V2(1,1)^2+V2(2,1)^2+V2(3,1)^2) v1 = 4.5825757 модуль v1
-->X=sqrt(x(1,1).^2+x(2,1).^2+x(3,1).^2) X = 4.5825757 модуль v2
Скорости движущихся объектов равны для обоих наблюдателей.
| --> x=linsolve(V1,v2) -3.5 -4 |
| v2 3.5 |
| Vn 1.5 |
--> v2=Vn+V2
--> x=linsolve(V1,v2)
--> X=sqrt(x(1,1).^2+x(2,1).^2+x(3,1).^2) X = 5.6789083 ¯\_(ツ)_/¯
--> v1=sqrt(Vn(1,1).^2+Vn(2,1).^2+Vn(3,1).^2) v1 = 5.6789083
| -->ra |
| -->rc 3.2 |
| -->rb |
| -->vo1 |
| -->rco 4.8 -6 |
| -->rao -3 |
| -->rbo -1.5 |
-->rbo=cross(rb,w)
| -->w 1.5 |
| -->vC 6.8 -5 |
| -->vA -2 |
| -->vB -0.5 |
-->vB=rbo+vo1
-->vC=rco+vo1
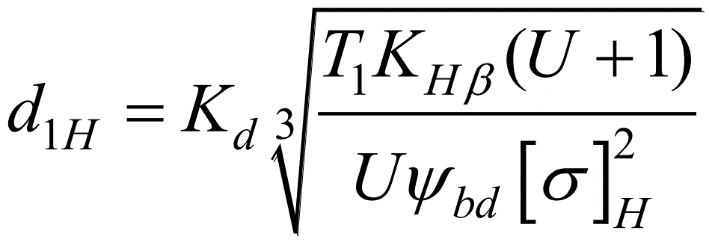3.3 Определить диаметр шестерни, исходя из контактной выносливости зубьев1 Используя формулу (рис. 3).
-->Kd=690 -->T1=100
-->Khb=1.12 -->U=5
| рис. 3 |
-->d1H = Kd*((T1*Khb*(U+1))/(U*psibd*sigmaH^2))^(1/3) d1H = 52.362984
-->T1=130 -->U=20
Изменение некоторых параметров.
-->d1H = Kd*((T1*Khb*(U+1))/(U*psibd*sigmaH^2))^(1/3) d1H = 54.660659
Вывод: в результате лабораторной работы получил базовые знания работы в среде MatLab/SciLabи научился функции и команды MatLab/SciLab для решения различного рода задач. Увидел несколько примеров практического применения программы, а так же примеры теоретических и визуальных расчетов.