К итоговому занятию
По математическому анализу
(1-й семестр 2014-2015 уч. год)
ВЫБЕРИТЕ ОДИН ВАРИАНТ ОТВЕТА
001. ПРИ УМНОЖЕНИИ МАТРИЦЫ РАЗМЕРНОСТИ
РАЗМЕРНОСТИ  НА МАТРИЦУ ПОЛУЧИЛАСЬ МАТРИЦА
НА МАТРИЦУ ПОЛУЧИЛАСЬ МАТРИЦА  РАЗМЕРНОСТИ
РАЗМЕРНОСТИ  . ТОГДА РАЗМЕРНОСТЬ МАТРИЦЫ
. ТОГДА РАЗМЕРНОСТЬ МАТРИЦЫ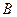 РАВНА…
РАВНА…
1.  2.
2.  3.
3.  4.
4. 
002. УСТАНОВИТЕ СООТВЕТСВИЕ МЕЖДУ ОПРЕДЕЛИТЕЛЯМИ И ИХ ЗНАЧЕНИЯМИ
| Определитель | Значение определителя |
1.  2.
2.  3.
3. 
|
1.  2.
2.  3.
3. 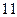 4.
4.  5.
5. 
|
ВЫБЕРИТЕ ОДИН ВАРИАНТ ОТВЕТА
003. МАТРИЦА 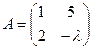 НЕ ИМЕЕТ ОБРАТНОЙ МАТРИЦЫПРИ
НЕ ИМЕЕТ ОБРАТНОЙ МАТРИЦЫПРИ  РАВНОМ…
РАВНОМ…
1. 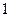 2.
2.  3.
3.  4.
4. 
004. ДАНА СИСТЕМА УРАВНЕНИЙ 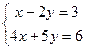 . ЧТОБЫНАЙТИ ЗНАЧЕНИЕ ПЕРМЕННОЙ
. ЧТОБЫНАЙТИ ЗНАЧЕНИЕ ПЕРМЕННОЙ  ПО ФОРМУЛАМ КРАМЕРА, ДОСТАТОЧНО ВЫЧИСЛИТЬ ОПРЕДЕЛИТЕЛИ…
ПО ФОРМУЛАМ КРАМЕРА, ДОСТАТОЧНО ВЫЧИСЛИТЬ ОПРЕДЕЛИТЕЛИ…
1.  и
и  2.
2.  и
и  3.
3.  и
и  4.
4.  ,
,  и
и 
005. ЕСЛИ 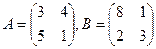 , ТО ЭЛЕМЕНТ
, ТО ЭЛЕМЕНТ  МАТРИЦЫ
МАТРИЦЫ РАВЕН
РАВЕН
1. 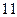 2.
2.  3.
3.  4.
4. 
006. ДАНА СИСТЕМА ЛИНЕЙНЫХ УРАВНЕНИЙ  . ТОГДА МАТРИЧНАЯ ФОРМА ЗАПИСИ ИМЕЕТ ВИД
. ТОГДА МАТРИЧНАЯ ФОРМА ЗАПИСИ ИМЕЕТ ВИД
1) 
| 2) 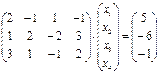
| 3) 
| 4) 
|
Ответ:
007. ВЕКТОРНЫМ ПРОИЗВЕДЕНИЕМ  или
или 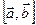 называется…
называется…
1. Вектор, перпендикулярный плоскости векторов  с модулем, определяемым формулой
с модулем, определяемым формулой 
2. число, обозначаемое  или
или  и равное
и равное  .
.
3. площадь параллелограмма, построенного на отрезках  с углом
с углом 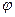 между ними:
между ними: 
008. СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ ВЕКТОРОВ  И
И  , ЕСЛИ
, ЕСЛИ  И УГЛОМ
И УГЛОМ  МЕЖДУ НИМИ, РАВНО…
МЕЖДУ НИМИ, РАВНО…
| 1) 12 | 2) 7 | 3) 6 | 4) 
| 5) 0 |
009. КООРДИНАТА  ТОЧКИ
ТОЧКИ  , ПРИНАДЛЕЖАЩЕЙ ПЛОСКОСТИ
, ПРИНАДЛЕЖАЩЕЙ ПЛОСКОСТИ  , РАВНА
, РАВНА
1) 
| 2) 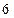
| 3) 
| 4) 
|
010. ЗНАЧЕНИЕ ПРЕДЕЛА 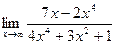 РАВНО…
РАВНО…
1)  2)
2) 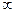 3) 0 4)
3) 0 4) 
011. ЧИСЛО ТОЧЕК РАЗРЫВА ФУНКЦИИ  РАВНО…
РАВНО…
1) 1; 2) 2; 3) 3; 4) точек разрыва не имеется
012. ЗАКОН ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ ИМЕЕТ ВИД:
 ,
,  – КООРДИНАТА ТОЧКИ В МОМЕНТ ВРЕМЕНИ
– КООРДИНАТА ТОЧКИ В МОМЕНТ ВРЕМЕНИ  . ТОГДА СКОРОСТЬ ТОЧКИ В МОМЕНТ ВРЕМЕНИ
. ТОГДА СКОРОСТЬ ТОЧКИ В МОМЕНТ ВРЕМЕНИ  РАВНА:
РАВНА:
ВАРИАНТЫОТВЕТОВ:
| 1) 12 | 2) 15 | 3) 5 | 4) 22 |
013. ПРОИЗВДНАЯ ЧАСТНОГО  РАВНА…
РАВНА…
ВАРИАНТЫОТВЕТОВ:
1) 
| 2) 
| 3) 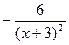
| 4) 
| 5) 1 |
014. ПРИ ИСПОЛЬЗОВАНИИ ПРАВИЛА ЛОПИТАЛЯ ПРИ ВЫЧИСЛЕНИИ ПРЕДЕЛА  ПОЛУЧИЛИ ПРЕДЕЛ ФУНКЦИИ
ПОЛУЧИЛИ ПРЕДЕЛ ФУНКЦИИ
1) 
| 2) 
| 3) 
| 4) 
|
ВЫБЕРИТЕ ВАРИАНТЫСОГЛАСНО ТЕКСТУ ЗАДАНИЯ
015. УСТАНОВИТЕ СООТВЕСТВИЕ МЕЖДУ ФУНКЦИЕЙ И ЕЁ ПРОИЗВОДНОЙ.
Функция имеет вид: 1.  2.
2.  3.
3. 
Производная функции равна:
1)  2)
2)  3)
3)  4)
4) 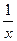 5)
5)  6)
6) 
ВЫБЕРИТЕ ОДИН ВАРИАНТ ОТВЕТА
016. ПРОИЗВОДНАЯ ФУНКЦИИ  ИМЕЕТ ВИД…
ИМЕЕТ ВИД…
1)  2)
2)  3)
3) 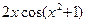 4)
4) 
017. ПРОИЗВОДНАЯ ТРЕТЬЕГО ПОРЯДКА ФУНКЦИИ  ИМЕЕТ ВИД…
ИМЕЕТ ВИД…
1) 
| 2) 
| 3) 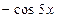
| 4) 
|
018. ДОСТАТОЧНОЕ УСЛОВИЕ ЭКСТРЕМУМА ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ СОСТОИТ В ТОМ, ЧТО…
1) производная данной функции при переходе через стационарную точку не меняет своего знака
2) производная данной функции при переходе через стационарную точку меняет свой знак с «+» на «-»
3) в точках возможного экстремума производная функции обращается в ноль или не определена
4) производная данной функции при переходе через стационарную точку меняет свой знак
019. УГЛОВОЙ КОЭФФИЦИЕНТ КАСАТЕЛЬНОЙ К ГРАФИКУ ФУНКЦИИ  В ТОЧКЕ С АБСЦИССОЙ
В ТОЧКЕ С АБСЦИССОЙ  РАВЕН …
РАВЕН …
ВАРИАНТЫОТВЕТОВ:
1) 
| 2) 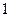
| 3) 
| 4) 
|
020. НЕОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ ФУНКЦИИ  – ЭТО…
– ЭТО…
1) функция  , для которой верно равенство:
, для которой верно равенство:  .
.
2) предел интегральных сумм  при неограниченном возрастании
при неограниченном возрастании  .
.
3) множество всех первообразных функции  .
.
4) функция  , для которой верно равенство:
, для которой верно равенство:  .
.
021. СРЕДИ ПРИВЕДЁННЫХ НИЖЕ ВЫСКАЗЫВАНИЙ НАЙДИТЕ ОШИБОЧНЫЕ
1) Интеграл постоянной величины равен нулю.
2) Постоянный множитель нельзя выносить за знак интеграла.
3) Определенный интеграл есть некоторое число.
4) Производная первообразной функции есть некоторое число.
022. МНОЖЕСТВО ПЕРВООБРАЗНЫХ ФУНКЦИИ 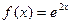 ИМЕЕТ ВИД…
ИМЕЕТ ВИД…
1)  2)
2)  3)
3) 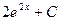 4)
4) 
УКАЖИТЕ ПОСЛЕДОВАТЕЛЬНОСТЬ ДЕЙСТВИЙ ПРИ ВЫЧИСЛЕНИИ ОПРЕДЕЛЁННОГО ИНТЕГРАЛА
ЧТОБЫВЫЧИСЛИТЬ ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ, НЕОБХОДИМО…
1) найти разность этих значений
2) вычислить значение первообразной при нижнем пределе интегрирования
3) найти одну из первообразных функций
4) вычислить значение первообразной при верхнем пределе интегрирования
5) найти первообразную функции
024. УСТАНОВИТЕ СООТВЕТСТВИЕ МЕЖДУ ИНТЕГРАЛОМ И ЕГО ЗНАЧЕНИЕМ
1.  2.
2.  3.
3.  4.
4. 
ВАРИАНТЫОТВЕТОВ:
1)  2)
2)  3)
3)  4)
4)  5)
5)  6)
6) 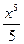
025. ВЫБЕРИТЕ ИЗ НИЖЕПРИВЕДЁННЫХ ИНТЕГРАЛОВ ТЕ, КОТОРЫЕ ИНТЕГРИРУЮТСЯ ПО ЧАСТЯМ
1.  2.
2.  3.
3.  4.
4.  5.
5. 