Линейные операции над матрицами.

Понятие матрицы. Типы матриц. Действия над матрицами. Определитель квадратной матрицы. Свойства определителей. Правила Сарруса.

Матрица	Матрицей называется множество чисел, образующих прямоугольную таблицу, которая содержит m строк и n столбцов.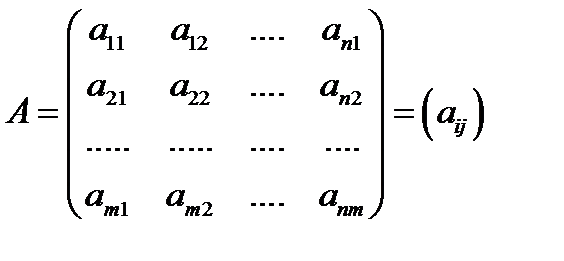
Виды матриц	Если число строк не равно числу столбцов 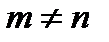, то матрица называется прямоугольной.
Если число строк равно числу столбцов то матрица называется квадратной. Число строк или столбцов квадратной матрицы называется ее порядком
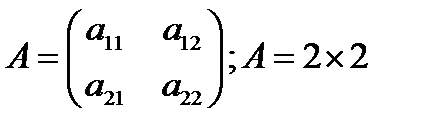
Квадратные матрицы, у которых отличны от нуля только элементы, находящиеся на главной диагонали называются диагональными матрицами.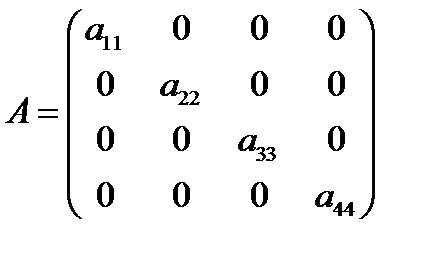
Если у диагональной матрицы все числа главной диагонали равны между собой, то такая диагональная матрица называется скалярной.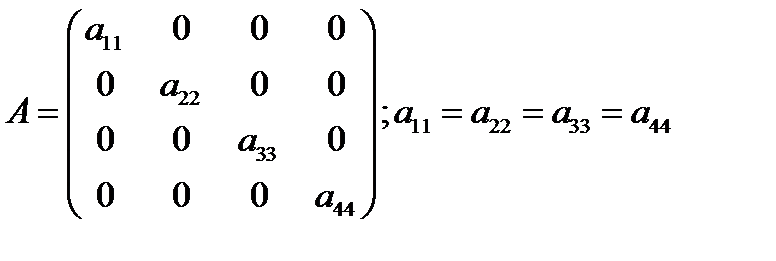
Если в скалярной матрице все числа главной диагонали равны единице, то матрица называется единичной.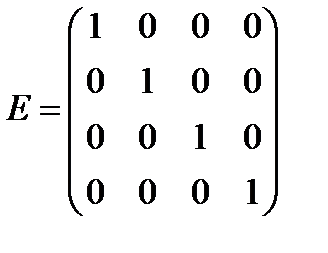
Матрица, все элементы которой равны нулю, называется нулевой матрицей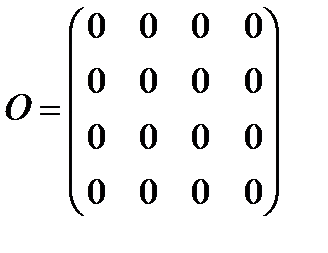
Если в прямоугольной матрице количество строк равно единице, а количество столбцов равно n, то получаем матрицу- строки.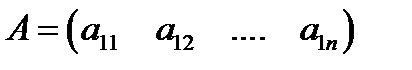
Если в прямоугольной матрице количество строк равно m, а количество столбцов равно единице, то получаем матрицу- столбца.
Матрица-строки и матрица-столбца называются векторами.
Равенство матриц	Две матрицы называются равными, если они имеют одинаковое число сток и одинаковое число столбцов и их соответствующие элементы равны. Равные матрицы обязательно имеют одно и то же строение: либо обе они прямоугольные типа , либо квадратные одного и того же порядка n.
Транспонирование матрицы	Если в матрице типа 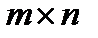переставить строки со столбцами, получим матрицу типа 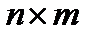, которую называют транспонированной матрицей.

Линейные операции над матрицами.

1. Суммой матриц А и В называется матрица С, элементы которой равны сумме соответствующих элементов матриц А и В. Складывать можно только матрицы, имеющие одинаковое строение: или прямоугольные типа , или квадратные порядка n.

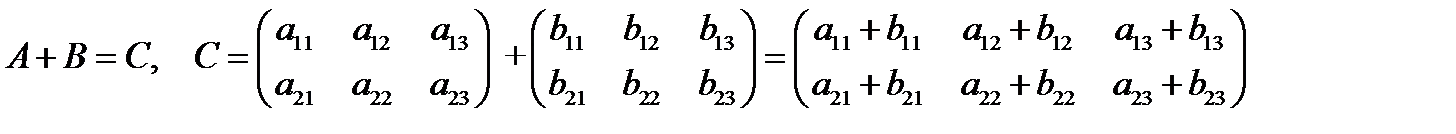
Свойства сложения:

1) Переместительный закон сложения: А+В=В+А, где А и В – либо квадратные матрицы одного типа n, либо прямоугольные матрицы одного типа .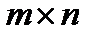

2) Сочетательный закон сложения (А+В)+С=А+(В+С) где А и В – либо квадратные матрицы одного типа n, либо прямоугольные матрицы одного типа .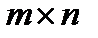

3) А+0=А, т.е. существует такая нулевая матрица (того же порядка или типа), что ее сумма с матрицей А любого типа равна матрице А.

4) Для любой матрицы А существует матрица (-А), такая, что А+(-А) = 0, т.е. матрица противоположная А.

2. Произведением матрицы А на число k называется такая матрица С, каждый элемент которой умножается на это число.

3. Произведение матрицы А на матрицу В есть матрица С.

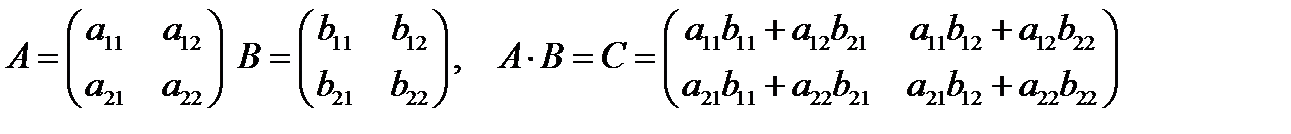
Правило умножения матриц: - чтобы найти элемент первой строки и первого столбца матрицы С, нужно каждый элемент первой строки матрицы А умножить на соответствующий элемент первого столбца матрицы В и полуженные результаты сложить;

- чтобы найти элемент первой строки и второго столбца матрицы С, нужно каждый элемент первой строки матрицы А умножить на соответствующий элемент второго столбца матрицы В и полуженные результаты сложить; и т.д.

- в общем случае: чтобы получить элемент, стоящий на пересечении i-й строки и j-го столбца матрицы-произведения, нужно все элементы i-ой строки матрицы А умножить на соответствующие элементы j-го столбца матрицы В и полученные произведения сложить.

Для прямоугольных матриц справедливы следующие правила:

1) умножение матрицы А на матрицу В имеет смысл только в том случае, когда число столбцов матрицы А равно числу строк матрицы В.

2) в результате умножения двух прямоугольных матриц получается матрица, содержащая столько строк, сколько строк в первой матрице, и столько столбцов, сколько столбцов во второй матрице.