1. Любой квадратной матрице А n-го порядка можно поставить в соответствие выражение det A, которое называется определителем (детерминантом) матрицы А (обозначается Δ или 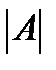 ), следующим образом:
), следующим образом:
1. n = 1 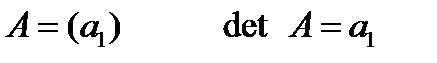
2. n = 2 
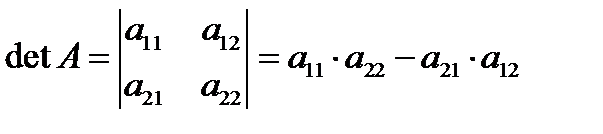
вычисление определителя 2-го порядка иллюстрируется схемой
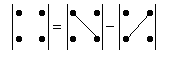
3. n = 3 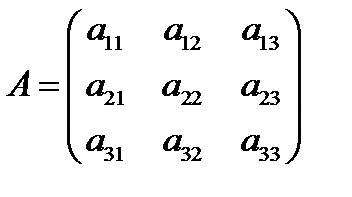
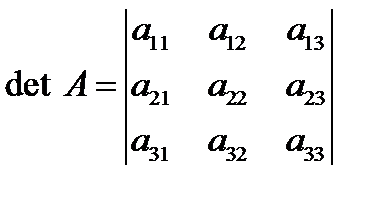

при вычислении определителя 3-го порядка удобно использовать правилом треугольников, которое символически можно записать так:

Три положительных члена определителя представляют собой произведения элементов главной диагонали и элементов, находящихся в вершинах двух равнобедренных треугольников, основания которых параллельны главной диагонали. Три отрицательных его члена есть произведения элементов побочной диагонали и элементов, находящихся в вершинах двух равнобедренных треугольников, основания которых параллельны побочной диагонали.

2. Основные свойства определителей:
- определитель не изменится, если его строки поменять местами с соответствующими столбцами (т.е. транспонировать) – это свойство называется свойством равноправности строк и столбцов;
- при перестановке двух строк (или столбцов) определитель изменит свой знак на противоположный;
- общий множитель всех элементов строки (или столбцов) можно вынести за знак определителя;
- определитель с двумя одинаковыми строками или столбцами равен нулю;
- если все элементы двух строк (столбцов) определителя пропорциональны, то определитель равен нулю;
- если к какой-либо строке (или столбца) определителя прибавить соответствующие элементы другой строки (или столбца), умноженные на одно и то же число, то определитель не изменит своей величины;
- треугольный определитель, у которого все элементы, лежащие выше (или ниже) главной диагонали, - нули, равен произведению элементов главной диагонали.
|
|
3. Минором 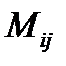 элемента
элемента  определителя называется такой новый определитель, который получается из данного определителя вычеркиванием строки и столбца, содержащих данный элемент.
определителя называется такой новый определитель, который получается из данного определителя вычеркиванием строки и столбца, содержащих данный элемент.
4. Алгебраическим дополнением элемента 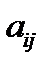 определителя D называется минор этого элемента, взятый со знаком
определителя D называется минор этого элемента, взятый со знаком  . Алгебраическое дополнение обозначается
. Алгебраическое дополнение обозначается  .
.
5. Теорема о разложении определителя по элементам строки и столбца: сумма произведений элементов любой строки (или столбца) определителя D на их алгебраические дополнения равна этому определителю
 .
.
Практическое занятие № 1. Решение задач по разделу "Линейная алгебра".
Задания:
1. Вычислить:
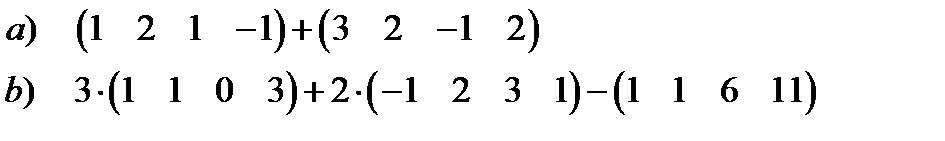
2. Даны матрицы А и В. Найти линейную комбинацию 2А +5 В
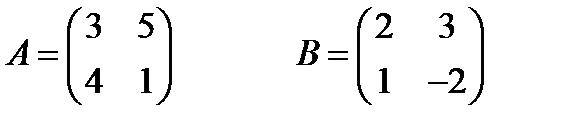
3. Даны матрицы А и В. Найти линейную комбинацию 5А – 2 В

4. Найти произведение матриц (если это возможно)
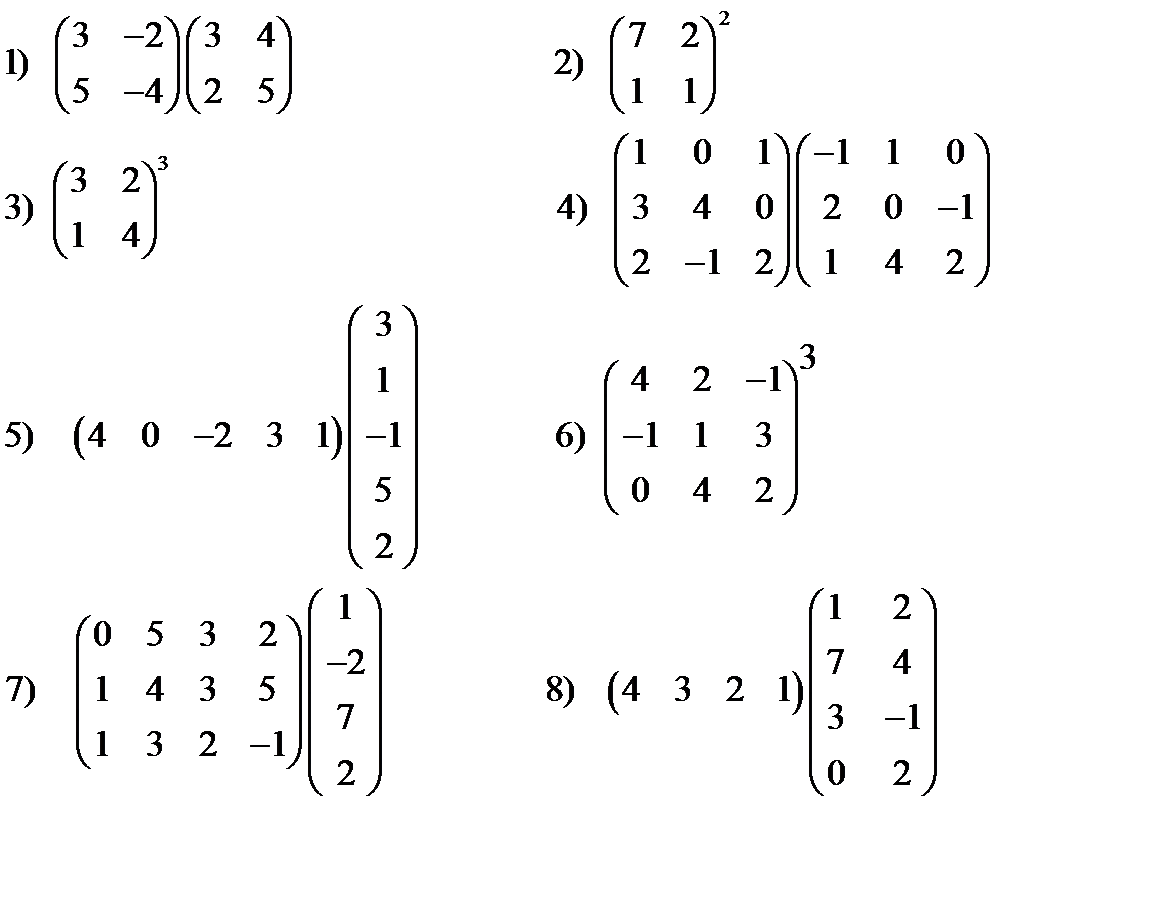
5. Найти значение матричного многочлена f(A):


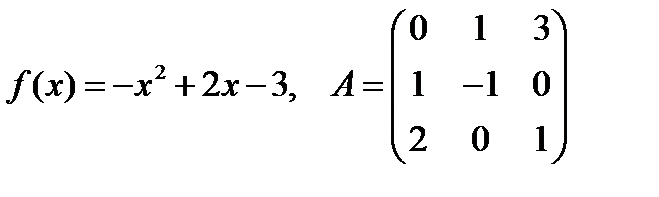
6. Найти произведение АВ:
а) А =  , В =
, В = 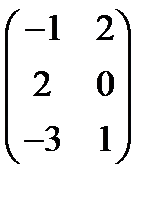 Ответ:
Ответ:  .
.
б) А = 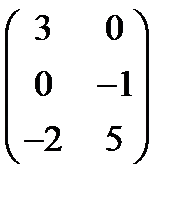 , В =
, В = 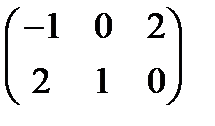 Ответ:
Ответ: 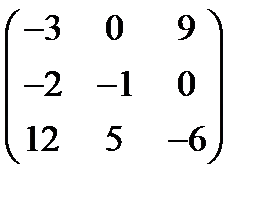 .
.
7. Вычислить С = А2 + 2В, где А = 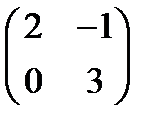 , В =
, В = 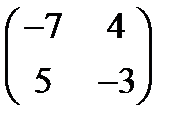 .
.
Ответ: 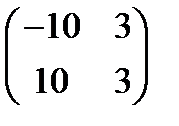 .
.
8. Найти АВ - ВА, где А = 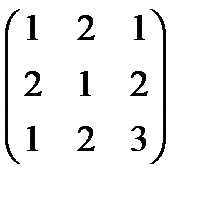 , В =
, В = 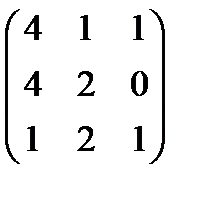
Ответ:  .
.
9. Найти АЕ, если А =  , Е =
, Е = 
Ответ: 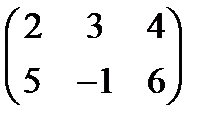 .
.
Домашнее задание.
1. Вычислить линейные комбинации матриц:
а) 2А - В, если А = 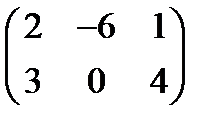 , В =
, В = 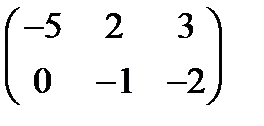 . Ответ:
. Ответ: 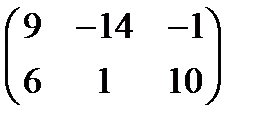 .
.
б) 3А + 2В, если А =  , В =
, В =  . Ответ:
. Ответ: 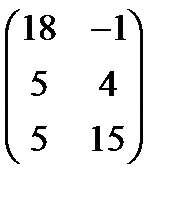 .
.
2. Найти произведение АВ:
а) А =  , В =
, В = 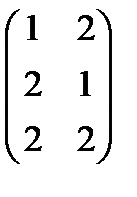 Ответ:
Ответ: 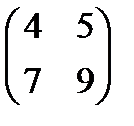 .
.
б) А =  , В =
, В = 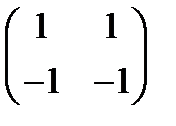 Ответ:
Ответ:  .
.
3. Найти  , если А =
, если А = 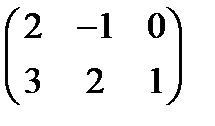 , В =
, В = 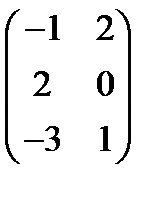 . Ответ:
. Ответ:  .
.
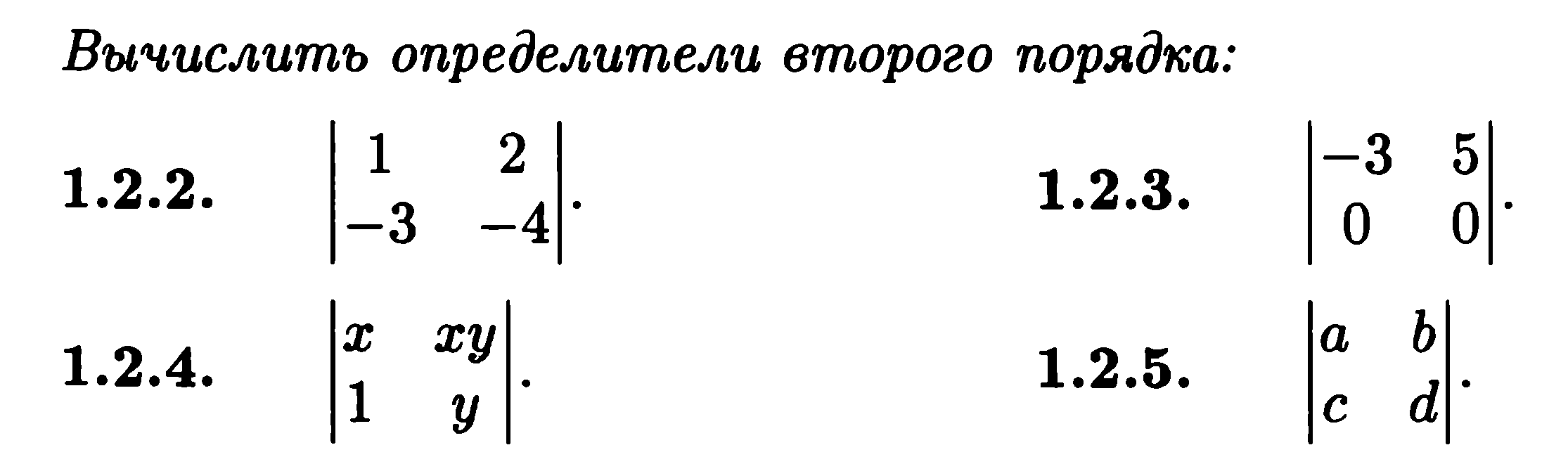

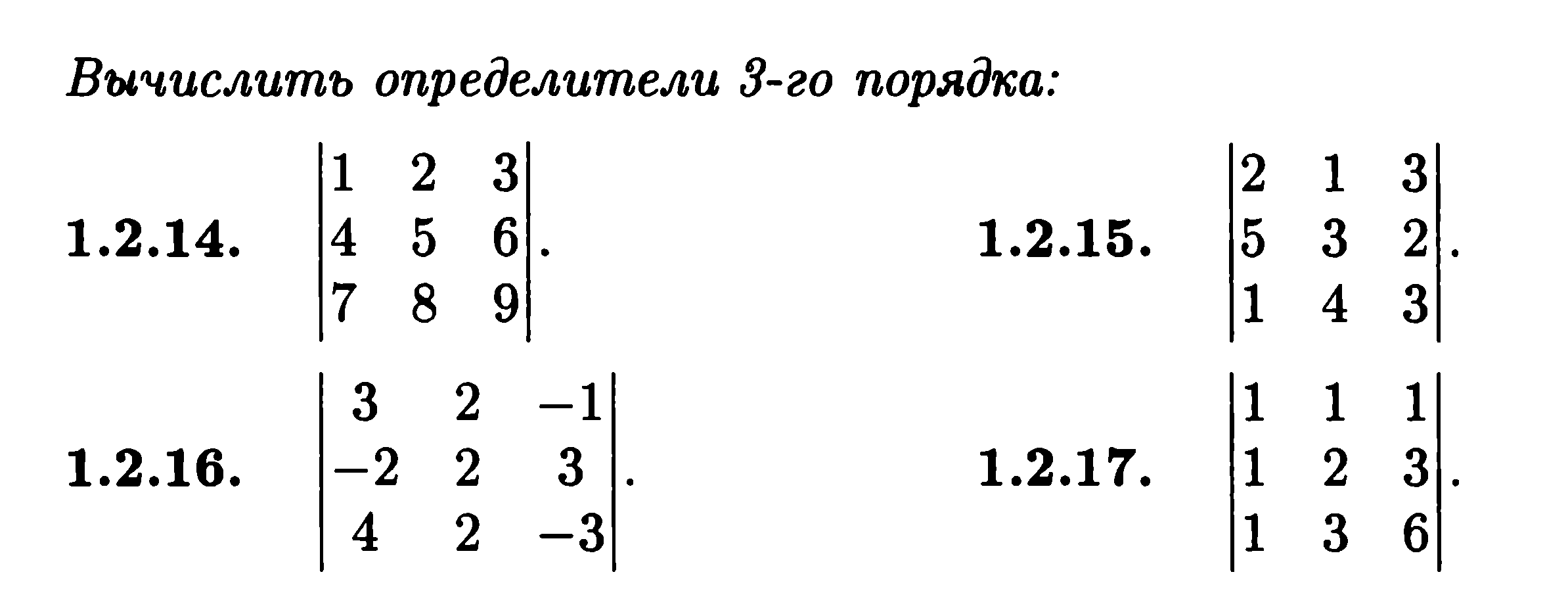

Домашнее задание.
1. Вычислить определители 2-ого порядка

2. Вычислить определители 3-ого порядка
