ТЕма: Понятие об ориентировании линий на местности.
План:
Изучите материал в соответствии с темой.
Составьте конспект лекции.
Выполненное задание направить в личном сообщении
https://vk.com/id108641434
Цель занятия: 1. Изучение рельефа на карте;
2. приобретение навыка по решению наиболее распространенных в строительной практике задач.
Задание 1: Построить профиль местности по линии, заданной на карте в выбранном Вами удобном масштабе(участок карты выбираете сами из интернет-источников).
Задание 2: Вычислить уклон заданной линии.
Понятие об ориентировании
При выполнении геодезических работ на местности, а также при решении инженерно-геодезических задач на топографических картах и планах возникает необходимость в определении положения линий местности относительно какого-либо направления, принимаемого за основное (исходное). Такое определение называется ориентированием.
Чаще всего за основное принимается направление меридиана, и положение линий местности определяется относительно сторон горизонта – севера, востока, юга и запада. Такое ориентирование называется ориентированием относительно стран света.
В геодезии при ориентировании за основное направление принимают направление осевого, истинного или магнитного меридианов. При этом положение линии определяют с помощью соответствующих углов ориентирования: дирекционного угла, истинного или магнитного азимута.
Дирекционные углы и осевые румбы, истинные и магнитные азимуты, зависимость между ними
Осевой (средний) истинный меридиан зоны часто принимают за основное направление. В этом случае положение линии местности относительно осевого меридиана определяет угол ориентирования, называемый дирекционным (рис. 16).
|
|
Дирекционный угол измеряется от северного направления осевого меридиана в направлении движения часовой стрелки через восток, юг и запад. Следовательно, градусная величина дирекционного угла может иметь любое значение от 0° до 360°.
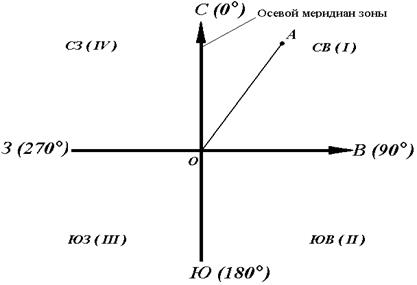
Рисунок 16 - Дирекционные углы
Для линии ОА её дирекционным углом в точке О является горизонтальный угол αОA между северным направлением осевого меридиана и направлением линии. Для линий ОВ, ОЕ и ОF – αОВ, αОE, αОF.
Таким образом, дирекционным углом является угол в горизонтальной плоскости, отсчитываемый от северного направления осевого меридиана по ходу часовой стрелки до данной линии.
В геодезии принято различать прямое и обратное направление линии (рис. 17). Так, если ВС считать прямым направлением линии, то СВ будет обратным направлением той же линии. В соответствии с этим αBC является прямым дирекционным углом линии ВС в точке М, а угол αCB – обратным дирекционным углом этой же линии в той же точке.
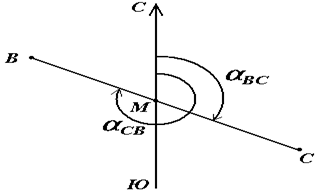
Рисунок 17 - Прямое и обратное направление линии
Из рисунка видно, что αCB = αBC + 180°, т.е. прямой и обратный дирекционные углы отличаются друг от друга на 180°.
Иногда для ориентирования линии местности пользуются не дирекционными углами, а румбами (рис. 18).
Осевым румбом называется острый горизонтальный угол, отсчитываемый от ближайшего направления осевого меридиана (северного или южного) до данной линии. Румбы обозначают буквой r с индексом, указывающим четверть, в которой находится румб.
|
|
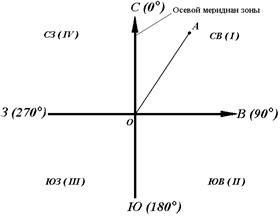
Рисунок 18 - Румбы и дирекционные углы
Название четвертей составлены из соответствующих обозначений главных точек горизонта: север (С), юг (Ю), восток (В), запад (З).
Зависимость между дирекционными углами и румбами определяется для четвертей по следующим формулам:
I четверть (СВ) r = α
II четверть (ЮВ) r = 180° – α
III четверть (ЮЗ) r = α – 180°
IV четверть (СЗ) r = 360° – α
Румб в точке М направления ВС называется прямым, а противоположного направления СВ – обратным. Прямой и обратный румб в одной и той же точке данной линии равны по численному значению, но имеют индексы противоположных четвертей.
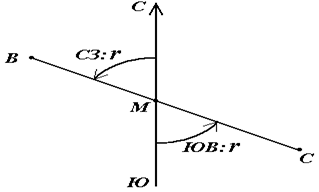
Рисунок 19 - Прямой и обратный румбы
Кроме осевого меридиана зоны при ориентировании линий местности за основное направление может приниматься направление истинного (географического) меридиана.
Истинный меридиан – линия пересечения земной поверхности с плоскостью, проходящей через отвесную линию и ось вращения Земли.
Положение линии местности относительно истинного меридиана определяется истинным азимутом или истинным румбом.
Истинный азимут линии – угол в горизонтальной плоскости, отсчитываемый от северного направления истинного меридиана по ходу часовой стрелки до данной линии (рис. 20).
Истинный румб линии – острый горизонтальный угол, отсчитываемый от ближайшего направления истинного меридиана (северного или южного) до данной линии.
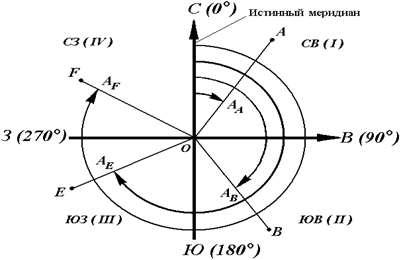
Рисунок 20 - Истинные азимуты
Истинный азимут A измеряется от 0° до 360°. Зависимость между истинными азимутами и румбами такая же, как и между дирекционными углами и осевыми румбами.
|
|
Истинные меридианы, проходящие через точки Земли с разной долготой, не параллельны между собой и сходятся на полюсах. Поэтому азимуты одной и той же прямой линии, определяемые относительно разных истинных меридианов, отличаются на величину γ (рис. 21), которую называют углом сближения меридианов. Его приближенное значение можно рассчитать по формулам:
γ = 0,54 · l · tg φ или γ = sin φ · Δλ,
где l – длина прямой линии между точками (км); φ – средняя широта линии; Δλ – разность долгот. При l = 1 км и широте Хабаровска φ = 48°28' угол сближения меридианов γ = 0,6' = 36".
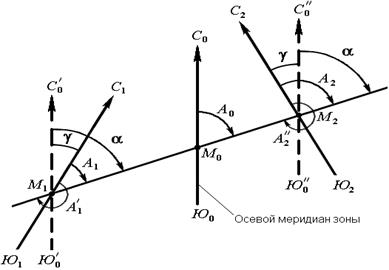
Рисунок 21 - Зависимость между истинным азимутом и дирекционным углом
Для перехода от дирекционного угла к истинному азимуту и наоборот необходимо знать угол сближения γ между осевым и истинным меридианом (рис. 21). Зависимость между истинным азимутом и дирекционным углом следующая
А = α + γ.
Если точка расположена к западу от осевого меридиана, то величину угла сближения γ между осевым и истинным меридианом принято считать отрицательной, если к востоку – положительной (рис. 21). Например, истинные азимуты линии при дирекционном угле α = 70° и углах сближения γ = – 0°50' для западной точки М1, γ = 0°50' для восточной – М2 соответственно равны
А1 = 70° – 0°50' = 69°50',
А2 = 70° + 0°50' = 70°50'.
Вопросы для проверки:
1. Понятие об ориентировании линий на местности.
2. Истинные и магнитные азимуты.
3. Дирекционный угол.
4. Румбы.
5. Формулы перехода от дирекционного угла к азимутам.
6. Формы связи между румбами и азимутами.