Используя исходные данные, записываем все заданные значения выборки в виде неубывающей последовательности значений случайной величины Х. Данный ранжированный ряд представлен в таблице 4.1.
Таблица 1.4.1.
Ранжированный ряд
Исходные данные
| 11,38 | 12,39 | 12,96 | 13,84 | ||||
| 11,62 | 12,44 | 12,98 | 13,95 | ||||
| 11,65 | 12,46 | 13,04 | 14,12 | ||||
| 11,69 | 12,5 | 13,05 | 14,16 | ||||
| 11,78 | 12,51 | 13,06 | 14,22 | ||||
| 12,58 | 13,1 | 14,24 | |||||
| 12,04 | 12,67 | 13,29 | 14,42 | ||||
| 12,05 | 12,67 | 13,37 | 14,44 | ||||
| 12,09 | 12,82 | 13,38 | 14,49 | ||||
| 12,09 | 12,83 | 13,38 | 14,7 | ||||
| 12,1 | 12,84 | 13,52 | 14,74 | ||||
| 12,1 | 12,85 | 13,53 | 14,81 | ||||
| 12,14 | 12,87 | 13,71 | 14,82 | ||||
| 12,21 | 12,88 | 13,74 | 14,97 | ||||
| 12,33 | 12,95 | 13,83 | 15,37 |
Интервал [11,38;15,37] содержащий все элементы выборки, разобьём на частичные интервалы, используя при этом формулу Стерджеса для определения оптимальной длины и границ этих частичных интервалов.
По формуле Стерджеса длина частичного интервала равна:
h= Xmax - Xmin = 3,99 = 0,7296 ≈ 0,6
1+ 3,322lg N 6,91
Для удобства и простоты расчетов выбираем h= 0,6 и вычисляем границы интервалов.
За начало первого интервала принимаем значение
Хо = Xmin – h/2 = 11,38 – 0,3 = 11,08
Далее вычисляем границы интервалов.
Х1 = Хо + h = 11,08 + 0,6 = 11,68
Х2 = Х1 + h = 11,68+ 0,6 = 12,28
Х3 = Х2 + h = 12,28+ 0,6 = 12,88
Х4 = Х3 + h = 12,88+ 0,6 = 13,48
Х5 = Х4 + h = 13,48+ 0,6 = 14,08
Х6 = Х5 + h = 14,08+ 0,6 = 14,68
Х7 = Х6 + h = 14,68+ 0,6 = 15,28
Х8 = Х7 + h = 15,28+ 0,6 = 15,88
Вычисление границ заканчивается как только выполняется неравенство Хп >Хmax
то есть Х8 = 15,88> Хmax = 15,37
По результатам вычислений составляем таблицу. В первой строке таблицы помещаем частичные интервалы, во второй строке – середины интервалов, в третьей строке записано количество элементов выборки, попавших в каждый интервал – частоты; в четвертой строке записаны относительные частоты и в пятой строке записаны значения плотности относительных частот или значения выборочной, экспериментальной функции плотности.
По результатам вычислений функции плотности, представленной в Таблице 1.4.2., можно сделать вывод, что мода имеет 1 локальный максимум в окрестности точки х = 12,58 и с частотой по n = 14
Оценку медианы находим, используя вариационный ряд для которого
n = 2k = 60 и k = 30:
Мe =1/2 (хk + хk+1) = ½ (х30 + х31) = ½ (12,95+12,96) = 12,96
Сравнение оценок Мe медианы = 12,96 и оценки математического ожидания Х = 13,11 показывает, что они отличаются на 15 %.
Таблица 1.4.2
 [ xi -1; xi)
| [11,08;11,68) | [11,68;12,28) | [12,28;12,88) | [12,88;13,48) | [13,48;14,08) | [14,08;14,68) | [14,68;15,28) | [15,28;15,88) |
| 11,38 | 11,98 | 12,58 | 13,18 | 13,78 | 14,38 | 14,98 | 15,58 |
| ni | ||||||||
| 0,0667 | 0,1833 | 0,2333 | 0,1833 | 0,1167 | 0,1167 | 0,0833 | 0,0167 |
| 0,1111 | 0,3056 | 0,3889 | 0,3056 | 0,1944 | 0,1944 | 0,1389 | 0,0278 |
Параметрическая оценка функции плотности распределения
Предположим, что статистические наблюдения принадлежат к
нормальному закону распределения с функцией плотности в виде:
Где 
и 
известны – они вычисляются по выборке.
= 0,975 = 13,11
Значения этой функции вычисляются для середины частичных интервалов вариационного ряда, т.е. при х = 
. На практике для упрощения вычислений функции 
, где i = 1,2,…, k, пользуются таблицами значений функции плотности стандартной нормальной величины.
Для этого вычисляем значения 
для i = 1,2,…, k, затем по таблице находим значение 
.
Z1 = (x1-x)/ σ = (11.38 – 13.11) /0,975 = -1,77
Z2 = (x2-x)/ σ = (11,98-13.11)/ 0,975 = -1,16
Z3 = (x3-x)/ σ = (12,58-13,11)/0,975 = -0,544
Z4 = (x4-x)/ σ = (13,18-13,11)/0,975 = 0,072
Z5 = (x5-x)/ σ = (13,78-13,11)/0,975 = 0,69
Z6 = (x6-x)/ σ = (14,38-13,11)/0,975 = 1,3
Z7 = (x7-x)/ σ = (14,98 – 13,11)/0,975 = 1,918
Z8 = (x8-x)/ σ = (15,58-13,11)/0,975 = 2,53
По таблице находим значение f(zi):
= 0,0833
= 0,2036
= 0,3448
= 0,3980
= 0,3144
= 0,1714
= 0,0644
= 0,0163
И после вычисляем функцию: 
φ ( 1) = 1 / σ= 0,0833/ 0,975 = 0,09
φ ( 2) = 2 / σ = 0,2036/ 0,975 = 0,21
φ ( 3) = 3 / σ = 0,3448/0,975 = 0,35
φ ( 4) = 4 / σ = 0,3980/0,975 = 0,41
φ ( 5) = 5 / σ = 0,3144/0,975 = 0,32
φ ( 6) = 6 / σ = 0,1714/ 0,975 = 0,18
φ ( 7) = 7 / σ = 0,0644/0,975 = 0,07
φ ( 8) = 8 / σ = 0,0163/ 0,975 = 0,02
Функция 
, вычисленная при заданных параметрах и в середине частичного интервала, фактически является теоретической относительной частотой, отнесенной к середине частичного интервала.
Поэтому для определения теоретической частоты 
, распределенной по всей ширине интервала, эту функцию необходимо умножить на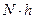 
.
где h = 0,6
рT1 = 0,6*0,09 = 0,054
рT2 = 0,6*0,21 = 0,126
рT3 = 0,6*0,35 = 0,21
рT4 = 0,6*0,41 = 0,246
рT5 = 0,6*0,32 = 0,192
рT6 = 0,6*0,18 = 0,108
рT7 = 0,6*0,07 = 0,042
рT8 = 0,6*0,02 = 0,012
где N = 60
nT1 = 0,09* 60 = 5,4
nT2 = 0,21*60 = 12,6
nT3 = 0,35*60 = 21
nT4 = 0,41*60 = 24,6
nT5 = 0,32*60 = 19,2
nT6 = 0,18*60 = 10,8
nT7 = 0,07*60 = 4,2
nT8 = 0,02*60 = 1,2
| [ xi -1; xi) | 
| 
| 
| 
| 
| 
| 
| 
|
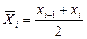
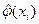
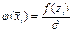
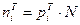
| [11,08;11,68) | 11,38 | 0,0667 | 0,1111 | -1,77 | 0,09 | 0,054 | 5,4 | |
| [11,68;12,28) | 11,98 | 0,1833 | 0,3056 | -1,16 | 0,21 | 0,126 | 12,6 | |
| [12,28;12,88) | 12,58 | 0,2333 | 0,3889 | -0,544 | 0,35 | 0,21 | ||
| [12,88;13,48) | 13,18 | 0,1833 | 0,3056 | 0,022 | 0,41 | 0,246 | 24,6 | |
| [13,48;14,08) | 13,78 | 0,1167 | 0,1944 | 0,69 | 0,32 | 0,192 | 19,2 | |
| [14,08;14,68) | 14,38 | 0,1167 | 0,1944 | 1,3 | 0,18 | 0,108 | 10,8 | |
| [14,68;15,28) | 14,98 | 0,0833 | 0,1389 | 1,918 | 0,07 | 0,042 | 4,2 | |
| [15,28;15,88) | 15,58 | 0,0167 | 0,0278 | 2,53 | 0,02 | 0,012 | 1,2 | |
| Σ | 0,99 |
Построим графики экспериментальной и теоретической плотности
нормального распределения (рис. 1.5.1).