ТЕма: Система плоских прямоугольных координат.
План:
Изучите материал в соответствии с темой.
2. Ответьте на вопросы.
Выполненное задание направить в личном сообщении
https://vk.com/id108641434
Геодезические координаты определяют положение точки земной поверхности на референц-эллипсоиде (рис.7).
Геодезическая широта B – угол, образованный нормалью к поверхности эллипсоида в данной точке и плоскостью его экватора. Широта отсчитывается от экватора к северу или югу от 0° до 90° и соответственно называется северной или южной широтой.
Геодезическая долгота L – двугранный угол между плоскостями геодезического меридиана данной точки и начального геодезического Гринвичского меридиана.
Долготы точек, расположенных к востоку от начального меридиана, называются восточными, а к западу – западными.
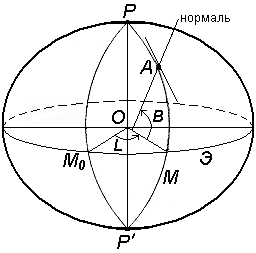
Рисунок 7 - Система геодезических координат
Астрономические координаты (для геодезии)
Астрономическая широта и долгота определяют положение точки земной поверхности относительно экваториальной плоскости и плоскости начального астрономического меридиана (рис.8).
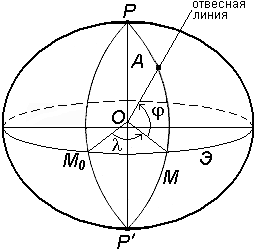
Рисунок 8 - Система астрономических координат
Астрономическая широта– угол, образованный отвесной линией в данной точке и экваториальной плоскостью.
Астрономическая долгота– двугранный угол между плоскостями астрономического меридиана данной точки и начального астрономического меридиана.
Плоскостью астрономического меридиана является плоскость, проходящая через отвесную линию в данной точке и параллельная оси вращения Земли.
Астрономическая широта и долгота определяются астрономическими наблюдениями.
Геодезические и астрономические координаты отличаются (имеют расхождение) из-за отклонения отвесной линии от нормали к поверхности эллипсоида. При составлении географических карт этим отклонением пренебрегают.
|
|
Географические координаты
Географические координаты – величины, обобщающие две системы координат: геодезическую и астрономическую, используют в тех случаях, когда отклонение отвесных линий от нормали к поверхности не учитывается (рис.9).
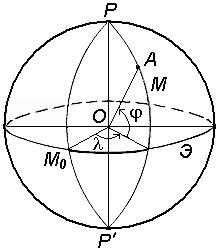
Рисунок 9 - Система географических координат
Географическая широта– угол, образованный отвесной линией в данной точке и экваториальной плоскостью.
Географическая долгота– двугранный угол между плоскостями меридиана данной точки с плоскостью начального меридиана.
Плоские прямоугольные геодезические координаты (зональные)
При решении инженерно-геодезических задач в основном применяют плоскую прямоугольную геодезическую и полярную системы координат.
Для определения положения точек в плоской прямоугольной геодезической системе координат используют горизонтальную координатную плоскость ХОУ (рис. 10), образованную двумя взаимно перпендикулярными прямыми. Одну из них принимают за ось абсцисс X, другую – за ось ординат Y, точку пересечения осей О – за начало координат.
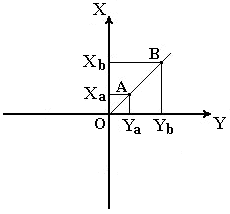
Рисунок 10 - Плоская прямоугольная система координат
Изучаемые точки проектируют с математической поверхности Земли на координатную плоскость ХОУ. Так как сферическая поверхность не может быть спроектирована на плоскость без искажений (без разрывов и складок), то при построении плоской проекции математической поверхности Земли принимается неизбежность данных искажений, но при этом их величины должным образом ограничивают. Для этого применяется равноугольная картографическая проекция Гаусса – Крюгера (проекция названа по имени немецких ученых, предложивших данную проекцию и разработавших формулы для её применения в геодезии), в которой математическая поверхность Земли проектируется на плоскость по участкам – зонам, на которые вся земная поверхность делится меридианами через 6° или 3°, начиная с начального меридиана (рис. 11).
|
|
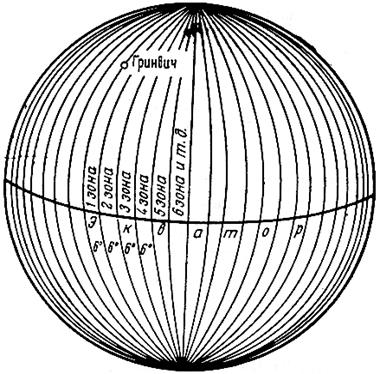
Рисунок 11 - Деление математической поверхности Земли на шестиградусные зоны
В пределах каждой зоны строится своя прямоугольная система координат. С этой целью все точки данной зоны проецируются на поверхность цилиндра (рис. 12, а), ось которого находится в плоскости экватора Земли, а его поверхность касается поверхности Земли вдоль среднего меридиана зоны, называемого осевым. При этом соблюдается условие сохранения подобия фигур на земле и в проекции при малых размерах этих фигур.
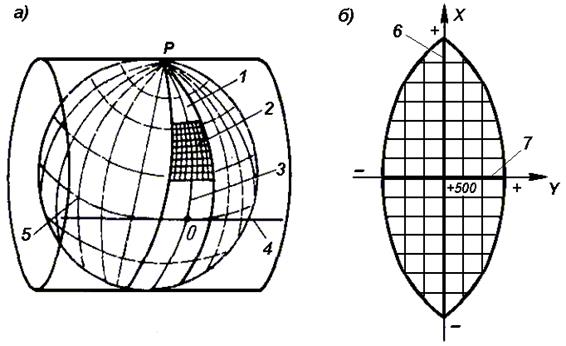
Рисунок 12 - Равноугольная картографическая проекция Гаусса – Крюгера (а) и зональная система координат (б):
1 – зона, 2 – координатная сетка, 3 – осевой меридиан, 4 – проекция экватора на поверхность цилиндра, 5 – экватор,6 – ось абсцисс – проекция осевого меридиана, 7 – ось ординат – проекция экватора
После проектирования точек зоны на цилиндр, он развертывается на плоскость, на которой изображение проекции осевого меридиана и соответствующего участка экватора будет представлена в виде двух взаимно перпендикулярных прямых (рис. 12, б). Точка пересечения их принимается за начало зональной плоской прямоугольной системы координат, изображение северного направления осевого меридиана – за положительную ось абсцисс, а изображение восточного направления экватора – за положительное направление оси ординат.
|
|
Для всех точек на территории нашей страны абсциссы имеют положительное значение. Чтобы ординаты точек также были только положительными, в каждой зоне ординату начала координат принимают равной 500 км (рис. 12, б). Таким образом, точки, расположенные к западу от осевого меридиана, имеют ординаты меньше 500 км, а к востоку – больше 500 км. Эти ординаты называют преобразованными.
На границах зон в пределах широт от 30° до 70° относительные ошибки, происходящие от искажения длин линий в этой проекции, колеблются от 1: 1000 до 1: 6000. Когда такие ошибки недопустимы, прибегают к трехградусным зонам.
На картах, составленных в равноугольной картографической проекции Гаусса – Крюгера, искажения длин в различных точках проекции различны, но по разным направлениям, выходящим из одной и той же точки, эти искажения будут одинаковы. Круг весьма малого радиуса, взятый на уровенной поверхности, изобразится в этой проекции тоже кругом. Поэтому говорят, что рассматриваемая проекция конформна, т. е. сохраняет подобие фигур на сфере и в проекции при весьма малых размерах этих фигур. Таким образом, изображения контуров земной поверхности в этой проекции весьма близки к тем, которые получаются.
Четверти прямоугольной системы координат нумеруются. Их счет идет по ходу стрелки от положительного направления оси абсцисс (рис.13).
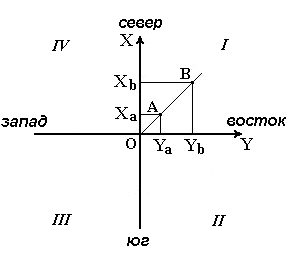
Рисунок 13 - Четверти прямоугольной системы координат
Если за начало плоской прямоугольной системы координат принять произвольную точку, то она будет называться относительной или условной.
Вопросы для проверки:
1. Географические координаты
2. Географическая широта
3. Географическая долгота
4. Плоская прямоугольная система координат
5. Четверти прямоугольной системы координат