Эта система счисления имеет основание S = 16. В общем виде шестнадцатеричное число выглядит следующим образом:
 ,
,
где 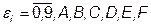 .
.

Шестнадцатеричная система счисления позволяет еще короче записывать многоразрядные двоичные числа и, кроме того, сокращать запись 4-разрядного двоичного числа, т.е. полубайта, поскольку 16=24. Шестнадцатеричная система также применяется в текстах программ для более краткой и удобной записи двоичных чисел.
Для перевода числа из двоичной системы счисления в шестнадцатеричную необходимо разбить это число влево и вправо от точки на тетрады и представить каждую тетраду цифрой в шестнадцатеричной системе счисления.
Пример.
Двоичное число 10101011111101(2) записать в шестнадцатеричной системе.
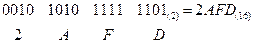
Пример.
Двоичное число 11101.01111(2) записать в шестнадцатеричной системе.

Для перевода числа из шестнадцатеричной системы счисления в двоичную, необходимо, наоборот, каждую цифру этого числа заменить тетрадой.
В заключение следует отметить, что перевод из одной системы счисления в другую произвольных чисел можно осуществлять по общим правилам, описанным в разделе “Двоичная система счисления”. Однако на практике переводы чисел из десятичной системы в рассмотренные системы счисления и обратно осуществляются через двоичную систему счисления.
Кроме того, следует помнить, что шестнадцатеричные и восьмеричные числа – это только способ представления больших двоичных чисел, которыми фактически оперирует процессор. При этом шестнадцатеричная система оказывается предпочтительнее, поскольку в современных ЭВМ процессоры манипулируют словами длиной 4, 8, 16, 32 или 64 бита, т.е. длиной слов, кратной 4. В восьмеричной же системе счисления предпочтительны слова, кратные 3 битам, например слова длиной 12 бит (как в PDP-8 фирмы DEC).
Двоичная арифметика
Правила выполнения арифметических действий над двоичными числами определяются арифметическими действиями над одноразрядными двоичными числами.

перенос в
старший разряд
Правила выполнения арифметических действий во всех позиционных системах счисления аналогичны.
Сложение
Как и в десятичной системе счисления, сложение двоичных чисел начинается с правых (младших) разрядов. Если результат сложения цифр МЗР обоих слагаемых не помещается в этом же разряде результата, то происходит перенос. Цифра, переносимая в соседний разряд слева, добавляется к его содержимому. Такая операция выполняется над всеми разрядами слагаемых от МЗР до СЗР.
Пример.
Сложить два числа в десятичном и двоичном представлении (формат – 1 байт).
Перенос (единицы) 11 1111111
Слагаемое 1 099(10) 01100011(2)
Слагаемое 2 095(10) 01011111(2)
Сумма 194(10) 11000010(2)
Операция получается громоздкая со многими переносами, но удобная для ЭВМ.
Вычитание
Операция вычитания двоичных чисел аналогична операции в десятичной системе счисления. Операция вычитания начинается, как и сложение, с МЗР. Если содержимое разряда уменьшаемого меньше содержимого одноименного разряда вычитаемого, то происходит заем 1 из соседнего старшего разряда. Операция повторяется над всеми разрядами операндов от МЗР до СЗР.
Поясним это примером.
Пример.
Вычесть два числа в десятичном и двоичном представлении (формат – 1 байт).
Заем (единица) 1 01100000
Уменьшаемое 109(10) 01101101(2)
Вычитаемое 049(10) 00110001(2)
Разность 060(10) 00111100(2)
Второй вариант операции вычитания – когда уменьшаемое меньше вычитаемого – приведен в разделе представления двоичных чисел в дополнительном коде.