Если к проводнику приложено внешнее электрическое поле, то на тепловое движение свободных электронов накладывается ещё направленное движение под действием сил электрического поля, что и порождает электрический ток.
При этом считается, что движение электронов под действием сил электрического поля подчиняется законам классической механики, а их столкновения с ионами кристаллической решётки металла являются неупругими.
Модель электронного газа даёт возможность теоретически объяснить природу сопротивления и вывести закон Ома для участка цепи, не содержащего источника тока, на основе классической электронной теории проводимости металлов.
Итак, пусть электрон движется с ускорением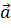 
в направлении, противоположном направлению напряжённости электрического поля. Так как движение электрона подчиняется законам классической механики, то его ускорение мы можем определить на основании второго закона Ньютона:
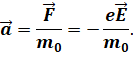
В записанной формуле m 0 — это масса электрона, а F — это постоянная сила, действующая на электрон со стороны электрического поля. Она равна произведению заряда электрона на напряжённость электрического в проводнике.
Тогда модуль средней скорости направленного движения электрона (она называется дрейфовой скоростью) линейно возрастает со временем:
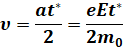
Здесь t * — это усреднённое время между двумя последовательными столкновениями электрона с ионами кристаллической решётки.
Дрейфовая скорость электрона не увеличивается в дальнейшем со временем, так как при столкновении с ионами кристаллической решётки электрон передаёт им кинетическую энергию, приобретённую в электрическом поле. Потом он опять ускоряется и процесс повторяется. В результате дрейфовая скорость электрона оказывается пропорциональной напряжённости электрического поля в проводнике.
|
|
Поскольку электрическое поле внутри однородного прямолинейного проводника с током однородное, то модуль напряжённости этого поля равен отношению напряжения между его концами к длине проводника:
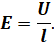
Тогда модуль средней скорости направленного движения электронов пропорционален напряжению между концами проводника: υ ~ U.
Теперь давайте с вами вспомним, что сила тока в проводнике пропорциональна модулю средней скорости направленного движения электронов:
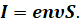
Но, как мы показали с вами выше, дрейфовая скорость пропорциональна разности потенциалов на концах проводника. Следовательно, сила тока пропорциональна разности потенциалов на концах проводника: I ~ U. В этом состоит качественное объяснение закона Ома на основе классической электронной теории проводимости металлов.
Для закрепления материала решим с вами небольшую задачу. Как изменится дрейфовая скорость электронов в проводнике, если при неизменной площади поперечного сечения и разности потенциалов на его концах, увеличить длину этого проводника в три раза?
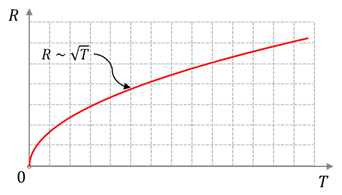
В заключении урока отметим, что построить удовлетворительную количественную теорию движения электронов в металле на основе законов классической механики невозможно. А дело всё в том, что условия движения электронов в металле таковы, что для его описания классическая механика Ньютона неприменима. Этот факт подтверждается, например, зависимостью сопротивлений металлов от температуры. Так в классической теории металлов, в которой движение электронов рассматривается на основе второго закона Ньютона, сопротивление проводника пропорционально квадратному корню из температуры.
|
|
