МЕТОДЫМАТЕМАТИЧЕСКОГО ОПИСАНИЯ ЛИНЕЙНЫХ
ЭЛЕМЕНТОВ И СИСТЕМ УПРАВЛЕНИЯ....................................................................... 30
2.1. Общие понятия о передаточных свойствах элементов и систем................... 30
2.2. Временные характеристики сигналов и типовых воздействий..................... 33
2.3. Статические характеристики элементов........................................................... 38
2.4. Линейные дифференциальные уравнения как динамические
характеристики............................................................................................................................ 45
2.5. Временные (переходные) характеристики....................................................... 48
2.6. Операторный метод и передаточная функция................................................. 52
2.7. Частотные характеристики................................................................................. 57
2.8. Статические и динамические характеристики типовых
соединений элементов................................................................................................................ 62
2.9. Элементарные операции машинного математического моделирования...... 68
Контрольные задания и вопросы.............................................................................. 70
ХАРАКТЕРИСТИКИ И МОДЕЛИ ТИПОВЫХ ДИНАМИЧЕСКИХ
ЗВЕНЬЕВ ЛИНЕЙНЫХ СИСТЕМ УПРАВЛЕНИЯ......................................................... 72
3.1. Классификация звеньев...................................................................................... 72
3.2. Безынерционное звено........................................................................................ 74
3.3. Инерционное звено первого порядка................................................................ 77
3.4. Инерционные звенья второго порядка.............................................................. 83
3.5. Интегрирующие звенья....................................................................................... 91
3.6. Дифференцирующие звенья............................................................................... 96
3.7. Звено запаздывания........................................................................................... 101
Контрольные задания и вопросы............................................................................ 104
4. ТИПОВЫЕ ОБЪЕКТЫУПРАВЛЕНИЯ............................................................ 105
4.1. Общие понятия об анализе объектов управления.......................................... 105
4.2. Генератор постоянного тока............................................................................. 107
4.3. Двигатель постоянного тока............................................................................ 111
Контрольные задания и вопросы............................................................................ 116
5. ПЕРЕДАТОЧНЫЕ ФУНКЦИИ СИСТЕМ УПРАВЛЕНИЯ (СУ)................. 118
5.1. Правила преобразования алгоритмических структур................................... 118
5.2. Пример составления передаточных функций и уравнений
динамики СУ............................................................................................................................. 124
5.3. Передаточные функции типовой одноконтурной СУ.................................. 127
Контрольные задания и вопросы............................................................................ 131
6. ТОЧНОСТЬ СИСТЕМ УПРАВЛЕНИЯ............................................................. 133
6.1. Общие понятия о точности управления.......................................................... 133
6.2. Точность статических и астатических систем стабилизации....................... 134
6.3. Динамическая точность СУ.............................................................................. 137
6.4. Типовые линейные алгоритмы управления................................................... 141
Контрольные задания и вопросы............................................................................ 143
7. АНАЛИЗ УСТОЙЧИВОСТИ ЛИНЕЙНЫХ СИСТЕМ УПРАВЛЕНИЯ..... 144
7.1. Понятие, виды и общее условие устойчивости............................................. 144
7.2. Алгебраический критерий устойчивости Гурвица....................................... 149
7.3. Частотный критерий устойчивости Найквиста............................................. 153
7.4. Влияние структуры и передаточного коэффициента СУ
на устойчивость......................................................................................................................... 160
Контрольные задания и вопросы............................................................................ 164
8. ОЦЕНКА КАЧЕСТВА УПРАВЛЕНИЯ............................................................. 166
8.1. Понятие и основные показатели качества...................................................... 166
8.2. Приближённая оценка качества по параметрам разомкнутого контура..... 176
8.3. Приближённая оценка качества по ЛАЧХ разомкнутого контура.............. 182
8.4. Интегральные показатели качества................................................................. 184
Контрольные задания и вопросы............................................................................ 188
Список дополнительной рекомендуемой литературы......................................... 189
ПРЕДИСЛОВИЕ
Предлагаемое студентам учебное пособие преследовало цель в краткой форме изложить основные разделы учебной дисциплины «Теория автоматического управления» (ТАУ) с учётом реального объёма учебного времени (≈ 80 часов, в том числе ≈ 40 часов аудиторных занятий), предусматриваемым учебным планом специальности.
Теория автоматического управления – учебная дисциплина, преподаваемая студентам указанной специальности в течение одного семестра. Целью преподавания ТАУ являются: формирование у студентов прочных знаний об общих принципах построения и законах функционирования автоматических систем управления, основных методах анализа непрерывных систем управления при регулярных внешних воздействиях, привитие студентам практических навыков по составлению функциональной и алгоритмической схем конкретной автоматической системы управления техническим объектом, определению передаточных функций и параметров отдельных конструктивных элементов системы, записи передаточных функций и уравнений статики и динамики линейной системы, расчёту статической и динамической точности управления, анализу устойчивости линейной системы, оценке показателей качества процесса управления.
Материал пособия сформировался в процессе длительного преподавания авторами курса ТАУ студентам, специализировавшимся в области автоматизации технологических процессов.
Основу учебного пособия составляют книги:
· Лукас В. А. Теория управления техническими системами: Учебное пособие для вузов. 4-е издание, исправленное. Екатеринбург: Из-во УГГУ, 2005. 677 с.
· Лукас В. А. Теория автоматического управления: Учебник для вузов. 2-е изд., перераб. и доп. М.: Недра, 1990. 416 с.
· Лукас В. А. Основы теории автоматического управления: Учебник для вузов. М.: Недра, 1977. 376 с.
СОКРАЩЕНИЯ И УСЛОВНЫЕ ОБОЗНАЧЕНИЯ
1. Сокращения основных терминов
ТАУ – теория автоматического управления
ТС – техническая система
ОУ- объект управления
УУ- управляющее устройство
СУ – система управления
ИО – исполнительный орган
ИУ – исполнительное устройство
Д – датчик
ОС – обратная связь
ПК – передаточный коэффициент
ПФ – передаточная функция
АФЧХ – амплитудно-фазовая частотная характеристика
АЧХ – амплитудно-частотная характеристика
ЛАЧХ – логарифмическая амплитудно-частотная характеристика
ФЧХ - фазо-частотная характеристика
2. Условные обозначения основных переменных и функций
x (t) – входной сигнал элемента СУ, выходной сигнал ОУ и СУ (управляемая величина)
y (t) – выходной сигнал элемента СУ, входной сигнал ОУ (управляющее воздействие)
x з(t) – задающее воздействие СУ
z (t) – возмущающее воздействие на СУ
e(t) – сигнал ошибки (рассогласования) в СУ
1(t) – единичное ступенчатое воздействие
d(t) – единичное импульсное воздействие
xm, ym – амплитудные значения сигналов x (t) и y (t)
p – оператор Лапласа, оператор дифференцирования
w - круговая частота, оператор преобразования Фурье
X (p) – изображение непрерывного сигнала x (t) по Лапласу
X (j w) – изображение непрерывного сигнала x (t) по Фурье
k – ПК звена (или соединения звеньев)
W (p) – ПФ звена (или соединения звеньев)
W (j w) – АФЧХ звена (или соединения звеньев)
А (w) – АЧХ звена (или соединения звеньев)
j(w) – ФЧХ звена (или соединения звеньев)
Ф(р) – ПФ замкнутой СУ
h (t) – переходная функция (характеристика) звена или СУ
w (t) – импульсная (весовая) функция (характеристика) звена или СУ
ВВЕДЕНИЕ
Теория автоматического управления (ТАУ) – научная дисциплина, предметом изучения которой являются информационные процессы, протекающие в системах управления техническими и технологическими объектами. ТАУ выявляет общие закономерности функционирования автоматических систем различной физической природы и на основе этих закономерностей разрабатывает принципы построения высококачественных систем управления.
При изучении процессов управления в ТАУ абстрагируются от физических и конструктивных особенностей систем и вместо реальных систем рассматривают их адекватные математические модели. Чем точнее (полнее) математическая модель соответствует физическим процессам, протекающим в реальной системе, тем совершеннее будет проектируемая система управления.
Основными методами исследования в ТАУ являются математическое моделирование, теория обыкновенных дифференциальных уравнений, операционное исчисление и гармонический анализ. Рассмотрим кратко каждый из них.
Метод математического моделирования, объединяющий самые разнообразные способы и приёмы описания и представления физических объектов и явлений, можно условно, схематично представить с помощью наиболее часто используемого приёма – графическим изображением простого объекта, имеющего один входной сигнал x (t) и один выходной сигнал y (t), в виде прямоугольника (рис. В. 1, а). Символ А внутри прямоугольника означает некоторый математический оператор (функцию, интеграл и т. п.), который связывает входной и выходной сигналы, меняющиеся во времени.

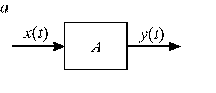
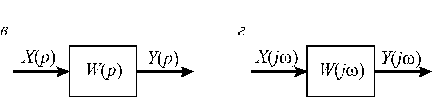
Рис. В.1. Схематичное представление математических методов, используемых в ТАУ
Теория обыкновенных дифференциальных уравнений, акцентирующая своё внимание на физические аспекты и приложения получаемых решений, служит главной методологической основой ТАУ, а сами обыкновенные дифференциальные уравнения – наиболее общей и полной формой математического описания элементов и систем управления. Дифференциальные уравнения связывают меняющиеся во времени входные и выходные переменные и их производные. В простейшем случае дифференциальное уравнение имеет вид
dy (t)/ dt = f [ x (t), y (t)]. (В.1)
Метод операционного исчисления, в основе которого лежит преобразование Лапласа
 (В.2)
(В.2)
позволяет алгебраизировть дифференциальные уравнения – перейти к так называемым операторным уравнениям, связывающим изображения X (p) и Y (p) входного и выходного сигналов через передаточную функцию W (p) (рис. В. 1, б)
W (p)= Y (p)/ X (p). (В.3)
Метод гармонического анализа основан на известном из курса математики преобразовании Фурье, имеющем вид
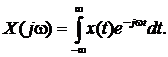 (В.4)
(В.4)
С помощью преобразования Фурье (В. 4) находят изображения X (j w) и Y (j w) входного и выходного сигналов x (t) и y (t), характеризующие частотные спектры этих сигналов. Изображения сигналов по Фурье связаны (рис.В. 1, в) частотной передаточной функцией
W(jw)=Y(jw)/X(jw). (В.5)
Все четыре метода, кратко представленные выше, образуют математический аппарат ТАУ. На его базе разработан комплекс «собственных» методов ТАУ, излагаемых в настоящем курсе.
ТАУ вместе с теорией построения и функционирования элементов систем управления (датчиков, регуляторов, исполнительных устройств) образует более широкую отрасль науки – автоматику. Автоматика в свою очередь является одним из разделов технической кибернетики. Техническая кибернетика изучает сложные автоматизированные системы управления технологическими процессами (АСУТП) и предприятиями (АСУП), построенные с использованием управляющих вычислительных машин (УВМ).
Техническая кибернетика наряду с биологической и социоэкономической – составная часть кибернетики, которую её родоначальник, американский математик Н. Винер, в 1948 году определил как науку об управлении и связи в технических системах и живых организмах.
Первые промышленные регуляторы появились в период 1765-1804 гг. (И. Ползунов, Дж. Уатт, Ж. Жаккар).
Первые теоретические исследования регуляторов появились в период 1868-1893 гг. (Дж. Максвелл, И. Вышнеградский, А. Стодола). Российский учёный и инженер И. А. Вышнеградский выполнил ряд научных исследований, в которых паровая машина и её регулятор впервые были проанализированы математическими методами как единая динамическая система. В становлении российской школы ТАУ большую роль сыграли работы А. А. Андронова, В. С. Кулебакина, И. Н. Вознесенского, Б. В. Булгакова, А. А. Фельдбаума, Б. Н. Петрова, Н. Н. Красовского, А. А. Воронова, Я. З. Цыпкина, В. С. Пугачёва, …
Развитие современной теории управления из так называемой «классической» теории регулирования, основанной на четырёх вышеупомянутых основных методах исследования ТАУ, и формирование её новейших методов схематично проиллюстрированы на рис. В. 2.
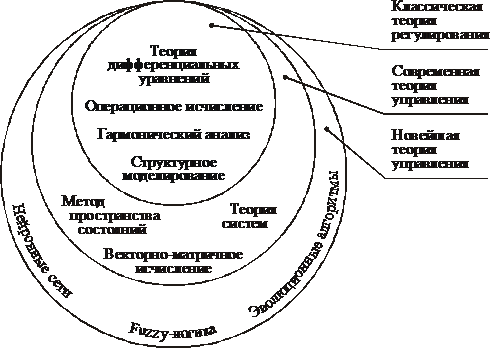 |
Рис. В.2. Развитие содержания и методологии теории управления
В настоящее время ТАУ наряду с новейшими разделами общей теории управления (исследование операций, системотехника, теория игр, теория массового обслуживания) играет важнейшую роль в совершенствовании и автоматизации управления технологическими процессами и производствами.