ЛАБОРАТОРНАЯ РАБОТА. Распределение молекул идеального газа по скоростям

ЛАБОРАТОРНАЯ РАБОТА

Распределение молекул идеального газа по скоростям

(распределение Максвелла)

Цель работы:

1. Изучение закона распределения молекул идеального газа по скоростям.

2. Построить распределение Максвелла для конкретного случая.

Краткая теория.

Среди различных состояний любой макроскопической системы особое место занимают равновесные состояния, то есть, состояния, в которых параметры системы не изменяются со временем. В газе, находящемся в состоянии равновесия, устанавливается некоторое стационарное, не меняющееся со временем, распределение молекул по скоростям, которое подчиняется вполне определенному статистическому закону. Этот закон был выведен Дж. Максвеллом, поэтому распределение молекул идеального газа по скоростям называют максвелловским распределением молекул по значениям модуля скорости. При выводе закона распределения молекул по скоростям Максвелла приняты следующие допущения: 1) газ состоит из очень большого числа N тождественных частиц (атомов, молекул), находящихся в состоянии непрерывного хаотичного движения; 2) температура газа постоянна; 3) никакие силовые поля на молекулы газа не действуют.

Закон распределения молекул по скоростям Максвелла описывается некоторой функцией f(v), которая называется функцией распределения молекул по скоростям. Если разбить диапазон скоростей v молекул на малые интервалы, равные dv, то на каждый такой интервал будет приходиться некоторое число молекул dN(v), имеющих скорости, заключенные в интервале от v до v+dv. Функция f(v) определяет относительное число молекул dN(v)/N, скорости которых лежат в указанном интервале:

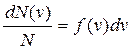(1)

где N – общее число молекул в системе. Максвелл установил конкретный вид функции f(v):

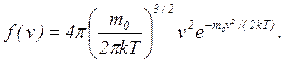(2)

Из этого выражения видно, что конкретный вид функции зависит от рода газа (массы его молекул m₀) и от температуры Т. График функции распределения приведен на рис.1.

Рис.1. Распределение Максвелла

Относительное число молекул dN(v)/N, скорости которых лежат в интервале от v до v+dv, находится как площадь заштрихованной полоски. Из графика следует, что функция распределения стремится к нулю при v ® 0 и v ® ¥ и проходит через максимум при некоторой скорости v_в, называемой наиболее вероятной, или вероятнейшей скоростью.

Продифференцировав функцию распределения Максвелла и приравняв производную нулю, можно показать, что

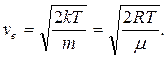(3)

C ростом температуры значение наиболее вероятной скорости растет, максимум функции распределения f(v) смещается вправо, при понижении температуры – наоборот, наиболее вероятная скорость уменьшается, максимум смещается влево. Площадь под кривой f(v) при любых изменениях температуры не меняется, так как не меняется общее число молекул в системе.

Наряду с наиболее вероятной скоростью, распределение молекул по скоростям можно характеризовать также средней 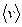скоростью (средней арифметической скоростью):

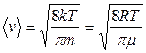(4)

Соотношение между средней квадратичной, наиболее вероятной и средней скоростями: <v> = 1.13 v_в, <v_кв> = 1.22 v_в.

Распределение молекул идеального газа по кинетическим энергиям определяет долю dN(e)/N из общего числа N молекул, которые имеют кинетические энергии 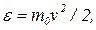заключенные в интервале от e до (e + de):

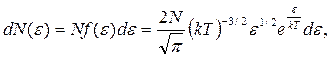(5)

где f(e) – функция распределения молекул по кинетическим энергиям.

 

Порядок проведения работы

1. По конкретному распределению молекул идеального газа по скоростям определить наиболее вероятную, среднюю и среднюю квадратичную скорости.

2. Рассчитать значение функции распределения молекул идеального газа по скоростям для десяти точек, включая вышеперечисленные.

3. Построить график распределения молекул идеального газа по скоростям и отметить на нем наиболее вероятную, среднюю и среднюю квадратичную скорости.

Варианты заданий

Вариант	Газ	t,0C	Вариант	Газ	t,0C
	O2			H2O (водяной пар)
	H2			CO
	N2			CO2
	H2O (водяной пар)			C2H2
	CO			NH3
	CO2			C2H4
	C2H2			CH4
	NH3			C2H8
	C2H4			C3H8
	CH4			O2
	C2H8			H2
	C3H8			N2
	O2			H2O (водяной пар)
	H2			CO
	N2			CO2
				O3

Таблица результатов вычислений

Газ - _______________ Т = ____ К

 

u, м/с
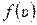