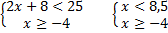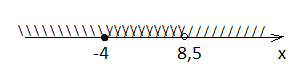Уравнения и неравенства с одной переменной
Решить уравнение – значит найти значение неизвестного, при котором оно обращается в верное равенство, или установить, что таких значений нет.
Например:
- уравнение  обращается в верное числовое равенство при
обращается в верное числовое равенство при  . Ответ:
. Ответ:  .
.
- уравнение  не имеет решений. Ответ: нет решений.
не имеет решений. Ответ: нет решений.
Решить неравенство – значит найти множество всех значений неизвестного или доказать, что их нет.
Например:
- неравенство  будет верным при любом
будет верным при любом  . Ответ:
. Ответ:  .
.
- двойное неравенство  не имеет общих решений для
не имеет общих решений для  . Ответ:
. Ответ: 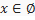
Рассматриваем:
- Степенные уравнения и неравенства (неизвестное 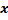 в основании степени
в основании степени 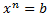 )
)
- Иррациональные уравнения и неравенства (неизвестное 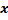 под знаком корня -ой степени
под знаком корня -ой степени 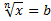 )
)
- Показательные уравнения и неравенства (неизвестное 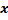 в показателе степени
в показателе степени  )
)
- Логарифмические уравнения и неравенства (неизвестное 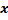 под знаком логарифма
под знаком логарифма 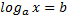 )
)
Степенные уравнения и неравенства
a) Линейные уравнения 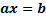 и неравенства
и неравенства 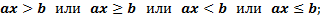
Решить уравнение


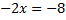
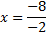
 Ответ: 4
Ответ: 4
| Решить неравенство:

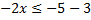
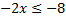
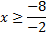 При делении неравенства на отрицательное число, знак неравенства меняется
При делении неравенства на отрицательное число, знак неравенства меняется
 Ответ:
Ответ: 
|
б) Квадратные уравнения 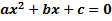 и неравенства
и неравенства 
Решить уравнения:
а) 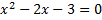
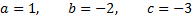
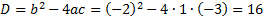
 Ответ:
Ответ: 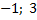 ----------------------------------------------------------
Неполные квадратные уравнения
б)
----------------------------------------------------------
Неполные квадратные уравнения
б) 
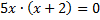 Произведение множителей равно нулю, когда или первый или второй множители равны нулю
Произведение множителей равно нулю, когда или первый или второй множители равны нулю

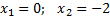 Ответ:
Ответ: 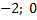 --------------------------------------------------------------
в)
--------------------------------------------------------------
в) 

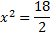

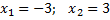 Ответ:
Ответ: 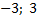
| Решить неравенства:
а) 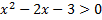 Сначала решаем уравнение
Сначала решаем уравнение
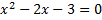
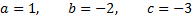
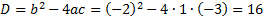
 Теперь раскладываем заданное неравенство на множители
Теперь раскладываем заданное неравенство на множители
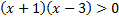 На числовой оси отмечаем промежутки положительного и отрицательного знака
На числовой оси отмечаем промежутки положительного и отрицательного знака
 Заданному неравенству удовлетворяют промежутки со знаком
Заданному неравенству удовлетворяют промежутки со знаком 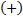 с невходящими границами
Ответ: с невходящими границами
Ответ: 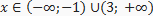 ----------------------------------------------------------------------
б)
----------------------------------------------------------------------
б) 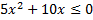
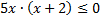 На числовой оси отмечаем промежутки положительного и отрицательного знака
На числовой оси отмечаем промежутки положительного и отрицательного знака
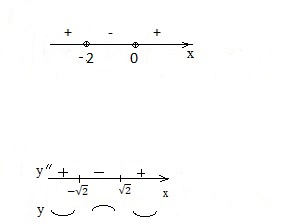 Заданному неравенству удовлетворяют промежутки со знаком
Заданному неравенству удовлетворяют промежутки со знаком  с входящими границами
Ответ: с входящими границами
Ответ: 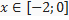 -------------------------------------------------------------------
в)
-------------------------------------------------------------------
в) 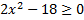 Раскладываем заданное неравенство на множители
Раскладываем заданное неравенство на множители
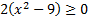
 На числовой оси отмечаем промежутки положительного и отрицательного знака
На числовой оси отмечаем промежутки положительного и отрицательного знака
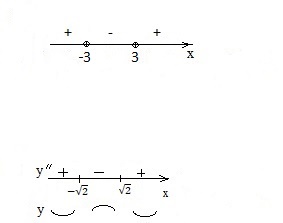 Заданному неравенству удовлетворяют промежутки со знаком
Заданному неравенству удовлетворяют промежутки со знаком 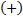 с входящими границами
Ответ: с входящими границами
Ответ: 
|
Иррациональные уравнения и неравенства
Алгоритм решения иррациональных уравнений и неравенств:
1) определить ОДЗ (область допустимых значений) подкоренного выражения;
2) возведение в квадрат обе части уравнения или неравенства, чтобы избавиться от квадратного корня.
Решить уравнение 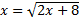 ОДЗ:
ОДЗ: 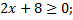
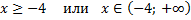 Возводим в квадрат обе части уравнения:
Возводим в квадрат обе части уравнения:

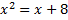 ;
Решаем уравнение ;
Решаем уравнение

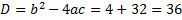 ; ;  Оба значения
Оба значения 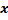 принадлежат ОДЗ.
Ответ: принадлежат ОДЗ.
Ответ: 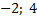 . .
| Решить неравенство  ОДЗ:
ОДЗ:  , тогда , тогда 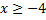 Возводим в квадрат обе части неравенства:
Возводим в квадрат обе части неравенства:
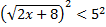 Объединяем ОДЗ и неравенство в систему и решаем её:
Объединяем ОДЗ и неравенство в систему и решаем её:
Ответ:
|
Показательные уравнения и неравенства
Порядок решения показательных уравнений и неравенств:
1) привести обе части уравнения или неравенства к одинаковому основанию степени.
2) Правило для уравнений: при равенстве оснований приравнять показатели степени;
Правило смены знака для неравенств:
а) для основания  записать неравенство для показателей степени, не изменяя знак неравенства;
записать неравенство для показателей степени, не изменяя знак неравенства;
б) для основания 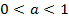 записать неравенство для показателей степени, изменяя знак неравенства.
записать неравенство для показателей степени, изменяя знак неравенства.
Решить показательные уравнения:
а) 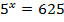 Приводим к одинаковому основанию
Приводим к одинаковому основанию
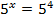 Основания равны, - приравниваем показатели степени
Ответ:
Основания равны, - приравниваем показатели степени
Ответ: 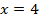
| б) 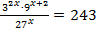 Приводим к одинаковому основанию
Приводим к одинаковому основанию
 Применяем правила действий со степенями
Применяем правила действий со степенями


 Основания равны, - приравниваем показатели степени
Основания равны, - приравниваем показатели степени
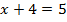 Ответ:
Ответ: 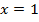
| в) 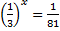 Приводим к одинаковому основанию
Приводим к одинаковому основанию
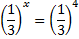 Основания равны, - приравниваем показатели степени
Ответ:
Основания равны, - приравниваем показатели степени
Ответ: 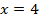
|
Решить показательные неравенства:
а) 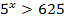 Приводим к одинаковому основанию
Приводим к одинаковому основанию
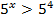 Основания равны, - записываем неравенство для показателей степени. Так как
Основания равны, - записываем неравенство для показателей степени. Так как  , то знак неравенства не меняется
Ответ: , то знак неравенства не меняется
Ответ: 
| б) 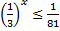 Приводим к одинаковому основанию
Приводим к одинаковому основанию
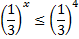 Основания равны, - записываем неравенство для показателей степени. Так как
Основания равны, - записываем неравенство для показателей степени. Так как 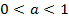 , то знак неравенства меняется
Ответ: , то знак неравенства меняется
Ответ: 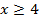 Действительно, например, при
Действительно, например, при  получаем получаем

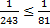 - верно! - верно!
|