На прошлом уроке изучались условные вероятности. Напомним, что в случайном опыте наступившие события могут менять вероятности других событий.
Вероятность события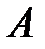 
при условии, что событие 
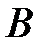произошло, называется условной вероятностью события 
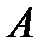при условии события 
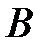. Обозначается эта вероятность 
.
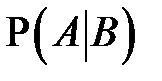Пример 1. Игральную кость бросают дважды. Событие А заключается в том, что при втором броске выпало не больше 3 очков. Приведите пример события, наступление которого:
а) не меняет вероятность события А.
б) уменьшает вероятность события А;
в) увеличивает вероятность события А.
| Рис. 1 |
Вероятность события А равна 0,5. Некоторое событие В не изменит вероятность события А, если при наступлении события В доля элементарных исходов, благоприятствующих А, не изменится и будет составлять половину всех исходов, благоприятствующих В. Таких событий много, например «на первой кости выпало 1 очко». Сопроводите объяснение рисунком (рис. 1), из которого видно, что из шести исходов, благоприятствующих В, ровно половина благоприятствует А.
| Рис. 2 |
Например, событие, изображённое тёмными квадратами на рис. 2, увеличивает вероятность наступления события А — его вероятность при условии В составляет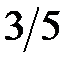 
, что больше, чем 0,5. Событие В можно описать как «сумма выпавших очков равна 6».
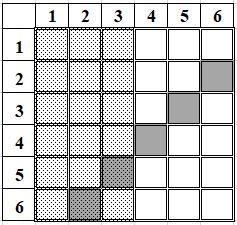
| Рис. 3 |
.
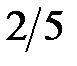Попробуйте придумать другие примеры для каждого из пунктов.
|
|
На предыдущем уроке было сформулировано правило умножения вероятностей:
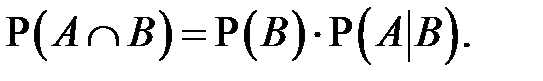
Можно поменять события местами и получить симметричное равенство:
.
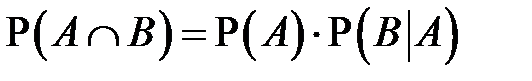Пример 2. Тест по истории сдало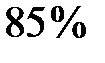 
учащихся школы, а тест по английскому языку — 
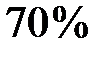учащихся. Известно, что тест по английскому языку сдало 
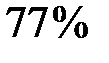тех, кто сдал тест по истории. Найдите вероятность того, что случайно выбранный ученик из тех, кто сдал тест по английскому, также сдал тест по истории.
Решение. Введем обозначения для событий: А «случайно выбранный ученик сдал тест по английскому», В «случайно выбранный ученик сдал тест по истории». Тогда по условию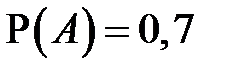 
, 
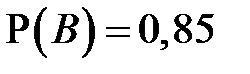и 
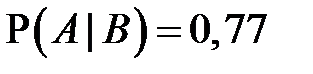. А найти нужно 
.
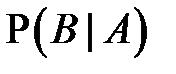Сравнивая две предыдущие формулы, получаем равенство
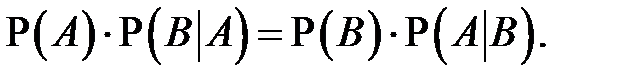
Подставляя в это равенство известные значения, находим:
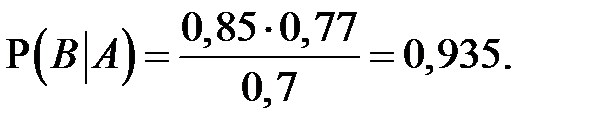
Пример 3. В некотором случайном опыте могут наблюдаться события A и B, причём P(A) = 0,75, P(B) = 0,8, а вероятность совместного наступления этих событий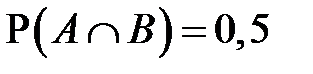 
. Найдите:
а) вероятность события A при условии, что наступило событие B;
б) вероятность события B при условии, что наступило событие A.
Решение. На предыдущем уроке мы получили формулу условной вероятности. Повторим этот вывод: если вероятность события В не равна нулю, то обе части равенства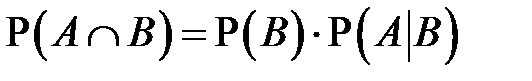 
можно разделить на 
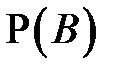. Получается формула условной вероятности:
.
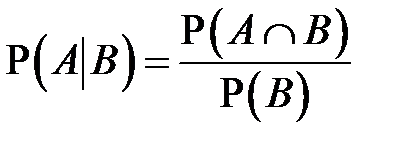Найдем условную вероятность события A при условии, что наступило событие B:
.
Если поменять события местами, то получим формулу для вычисления условной вероятности события B при условии, что наступило событие A:
.
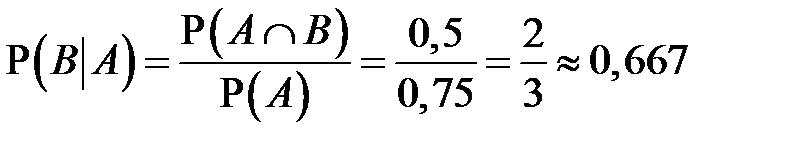Разобранные в двух последних примерах задачи можно решить и без формул, но решения будут многословными, поскольку придётся рассматривать отдельно все элементарные события. Формулы позволяют выразить одни вероятности через другие, не обсуждая в подробностях, как именно устроен случайный опыт.
|
|
Попробуете решить задачи самостоятельно и проверить получившиеся ответы.
Задача 1. В некотором случайном опыте могут наступить события А и В. Найдите:
а) вероятность события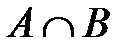 
, если P(B) = 0,8, P(A|B) = 0,6;
б) условную вероятность P(A|B), если P(B) = 0,25, P(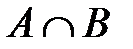
) = 0,23.
Ответ: а) 0,48; б) 0,92.
Задача 2. В некотором случайном опыте известны следующие вероятности событий: P(M | N) = 0,42, P(M) = 0,3, P(N) = 0,1. Найдите условную вероятность события N при условии, что событие М наступило.
Ответ: 0,14.
Задача 3. Тест по обществознанию сдали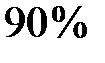 
учащихся школы, а тест по химии сдали 
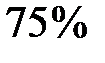учащихся. При этом известно, что тест по химии сдали 
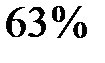тех, кто сдал тест по обществознанию. Найдите вероятность того, что ученик, случайно выбранный из тех, кто сдал тест по химии, также сдал тест по обществознанию.
Ответ: 0,756.
Задача 4. В некотором случайном эксперименте известны следующие вероятности: P(L) = 0,4, P(R) = 0,5, P(R|L) = 0,25. Найдите вероятность объединения событий R и L.
Ответ: 0,8
Задача 5. Рассеянный Учёный проводил исследование и в некотором случайном эксперименте у него получились следующие вероятности: P(N) = 0,44, P(M) = 0,8, P(N|M) = 0,65. Не ошибся ли он?
Решение: Ошибся.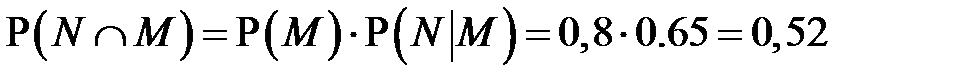 
, что больше, чем P(N). Вероятность пересечения событий не может быть больше вероятности любого из этих событий.
Задача 6. В некотором случайном эксперименте наблюдают два события A и B с известными вероятностями: P(A) = 0,75, P(B) = 0,6. Известно также, что в случае наступления события В вероятность наступления события A не меняется. Найдите вероятности событи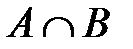й 
и 
.
|
|
Ответ: а) 0,45; б) 0,9.
Выводы и итоги урока. Правило умножения вероятностей и формула условной вероятности позволяют решать многие задачи, не разбираясь подробно в том, как именно устроен эксперимент. Они верны не только для опытов с равновозможными элементарными событиями, но и вообще для любых случайных опытов. Это делает изученные формулы удобным инструментом решения задач.
Домашнее задание
1. Игральную кость бросают дважды. Событие А заключается в том, что при первом броске выпало не меньше очков, чем при втором. Приведите пример события, наступление которого:
а) уменьшает вероятность события А;
б) увеличивает вероятность события А.
2. В классе 30 человек. Известно, что пятёрку и по физике и по математике в четверти получили только четверо их них. При этом известно, что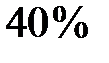 
тех, кто имеет 5 по математике, также отличник по физике. Найдите вероятность того, что случайно выбранный ученик класса имеет пятёрку по математике.
3. В некотором случайном опыте могут наблюдаться события A и B, причём P(A) = 0,45, P(B) = 0,4, а вероятность совместного наступления этих событий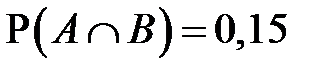 
. Найдите:
а) вероятность события A при условии, что наступило событие B;
б) вероятность события B при условии, что наступило событие A.
4. В коробке некоторое количество цветных карандашей, пять из которых —красные. Известно, что вероятность вытащить наугад из коробки два красных карандаша равна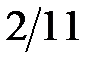 
. Сколько всего в коробке карандашей?
5*. В некотором случайном опыте наступление события B увеличивает вероятность события A Докажите, что в этом случае наступление события A увеличивает вероятность события B.