Основной анализ
Дано:
1. Схема (источник (импульсный), R, L, C)
2. Номиналы (см. рисунок 14)
Необходимо:
Найти время установления
Решение:
Для начала, зададим параметры импульсного источника и покажем окно, где задаются эти параметры на рисунке 27. Форму сигнала покажем на рисунке 28. Файл – LFF 10 (Time).cir.
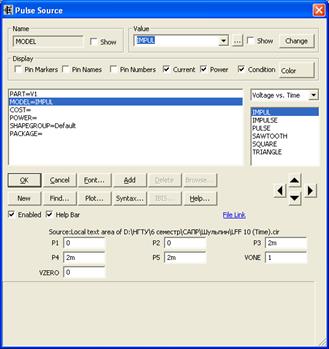
Рисунок 27. Окно задания параметров модели импульсного источника сигнала

Рисунок 28. Форма сигнала импульсного источника
Теперь найдем время установления – как 0.95 от установившегося значения. Результат покажем на рисунке 29.

Рисунок 29. Время установления ФНЧ
Как видно из рисунка 29 – время установления ФНЧ – 670 ± 10 микросекунд.
Температурный анализ
Дано:
1. Схема (источник (импульсный), R, C, L)
2. Номиналы (см. рисунок 15)
3. Температурные коэффициенты R, C, L = 0.001
Необходимо:
Рассчитать коэффициент влияния температуры на изменение времени установления
Решение:
Температурные коэффициенты для моделей R, C и L были заданы в пункте 2.1.
Определим коэффициент влияния температуры на изменение времени установления, задав в окне AC Analysis предел изменения температур от -40 Cº до 40 Cº (с шагом изменения 20 Cº). Вид окон задания температурных коэффициентов и пределов изменения температуры такой же, как на рисунках 16 и 17. Изменение времени установления в зависимости от температуры, покажем на рисунке 30. Файл – LFF 11 (Time Temp).cir.
|
|
|



Рисунок 30. Изменение времени установления в зависимости от температуры
40 Сº = 685 ± 10 мкс
20 Сº = 660 ± 10 мкс
27 Сº = 670 ± 10 мкс
αУСТ =  = 0,0019 = 0,002
= 0,0019 = 0,002
Статистический анализ
Прямая задача
Дано:
1. Схема (источник, R, C, L)
2. Номиналы (см. рисунок 15)
3. Допуски для элементов ΔR=20%, ΔC=20%, ΔL=25%
4. Вид закона распределения отклонения внутренних параметров от номинального значения (гауссовский, равномерный, наихудший случай)
Необходимо:
1. Найти среднее значение времени установления
2. Получить δ (среднее квадратичное отклонение) разброса значений времени установления от его среднего значения
Решение:
Допуски моделей R, C и L были заданы и откорректированы в пункте 2.1.
На рисунке 31 покажем, как изменяется время установления при изменении значений элементов в пределах их допусков (для гауссовского распределения и 500 итераций). Файл – LFF 12 (Time Common Stat).cir.



|
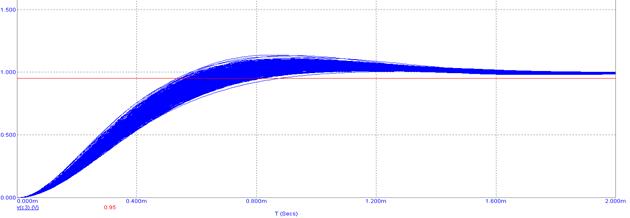
Рисунок 31. Пример изменения времени установления
Теперь проведем статистический анализ с использованием метода Монте-Карло для разных законов распределения (гистограммы не изображаются, потому что они отражают особенности законов распределения а не времени установления или других характеристик ФНЧ, и были указаны в пунке 2.1):
1. Гауссовский
| Число итераций | |||
| Среднее значение | 652,557*10-6 | 656,973*10-6 | 656,677*10-6 |
| δ | 56,433*10-6 | 59,247*10-6 | 59,620*10-6 |
· Среднее значение = 656 мкс
· δ =59 мкс
2. Равномерный
| Число итераций | |||
| Среднее значение | 661,416*10-6 | 671*10-6 | 662,301*10-6 |
| δ | 90,56*10-6 | 91*10-6 | 92,576*10-6 |
· Среднее значение = 662 мкс
· δ = 91 мкс
3. Наихудший случай
| Число итераций | |||
| Среднее значение | 700*10-6 | 678*10-6 | 683*10-6 |
| δ | 178*10-6 | 170*10-6 | 168*10-6 |
· Среднее значение = 683 мкс
· δ = 170 мкс
Обратная задача
Дано:
1. Схема (источник, R, C, L)
2. Номиналы (см. рисунок 15)
3. Вид закона распределения отклонения внутренних параметров от номинального значения (гауссовский, равномерный, наихудший случай)
4. δУСТ выходной характеристики от номинального значения (см. пункт 1.2)
Определить:
Допуски элементов, обеспечивающих это отклонение
По ТЗ: δТЗ (УСТ) = 50 мкс (см. пункт 1.2)
Используем алгоритм, описанный выше, в пункте 2.1. Подбор допусков по шагам:
1. δТЗ (УСТ)=50 мкс, δРАС=57,387 Гц, ∆R=20%, ∆C=20%, ∆L=25%
δРАС>δТЗ
Для R3: RН=1 Ом, RН-∆=0,8 Ом, RН+∆=1,2 Ом. Влияние изменения значений R3 в пределах допуска на изменение времени установления, покажем на рисунке 32.
|

Рисунок 32. Коэффициент влияния R3 на изменение времени установления
Для C3: CН=150 мкФ, СН-∆=105 мкФ, СН+∆=195 мкФ. Влияние изменения значений C3 в пределах допуска на изменение времени установления, покажем на рисунке 33.
|
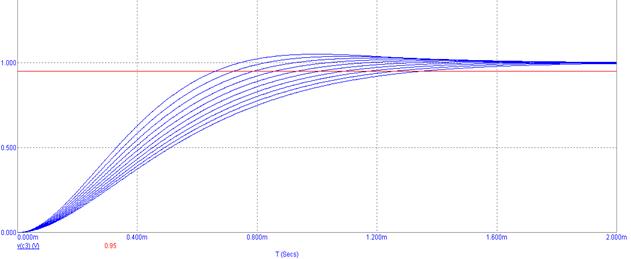
Рисунок 33. Коэффициент влияния C3 на изменение времени установления
Для L2: LН=700 мкГн, LН-∆=525 мкГн, LН+∆=875 мкГн. Влияние изменения значений L2 в пределах допуска на изменение времени установления, покажем на рисунке 34.

|
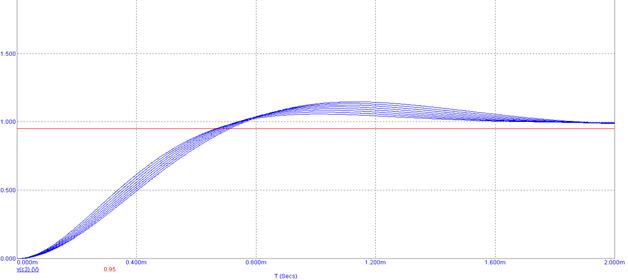
Рисунок 34. Коэффициент влияния L2 на изменение времени установления
∆fПП ∆C >> ∆fПП ∆R >>∆fПП ∆L, поэтому уменьшаем ∆C с 20% до 10%
3. δТЗ (УСТ)=50 мкс, δРАС=38,294 мкс, ∆R=20%, ∆C=10%, ∆L=25%
δРАС<δТЗ
На этом подбор допусков заканчиваем: ∆R=20%, ∆C=10%, ∆L=25%. Файл – LFF 13 (Time Reverse Stat).cir.