Основной анализ
Дано:
Структура ФНЧ
Необходимо:
1. Собрать схему и выбрать значения элементов
2. Построить АЧХ и добиться наиболее крутого перехода АЧХ
3. Установить необходимую полосу пропускания (см. пункт 1.2)
Решение:
1. Для начала построим в MicroCap схему ФНЧ, имеющего ТП структуру и отобразим ее на рисунке 2. Файл – LFF 1 (Original).cir.

Рисунок 2. Схема ФНЧ, имеющего ТП структуру
2. Необходимо, чтобы фильтр в полосе пропускания обеспечивал значение амплитуды сигнала, равное 1, в полосе запирания – 0, а переход между ними был как можно круче (спад дБ/октаву был как можно больше (по модулю)). Для этого и используются в схеме катушки индуктивности и дополнительные конденсаторы.
Снимем АЧХ с конденсаторов C1, C2 и C3, чтобы убедиться в том, что переход изменяется по мере добавления в схему катушек индуктивности и конденсаторов. Вид окна AC Analysis показан на рисунке 3, а результат - на рисунках 4 и 5. Файл – LFF 2 (dB).cir.

Рисунок 3. Вид окна AC Analysis

Рисунок 4. АЧХ снятая с C1, C2 и C3
|
|
|


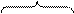
|
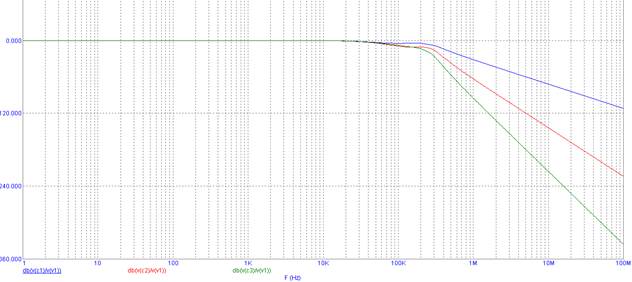
Рисунок 5. АЧХ снятая с C1, C2 и C3 (в дБ)
Теперь в режиме степпинга подберем такие значения катушек индуктивности, которые обеспечат наиболее крутой переход АЧХ ФНЧ.
Режим степпинга в MicroCap используется для моделирования при изменении значения номинала одного из элементов в определенном интервале. В данном случае, мы снимаем АЧХ при изменении значения катушки индуктивности L1 от 1 мкГн до 10 мкГн с шагом 1 мкГн. Вид окна Stepping показан на рисунке 6, а результат – на рисунке 7.

Рисунок 6. Вид окна Stepping
|
|
|
|
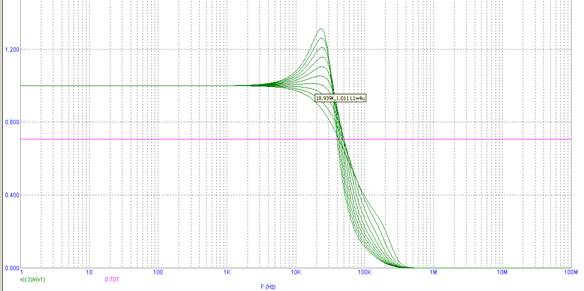
Рисунок 7. АЧХ c C3 при изменении L1 от 1u до 10u
Как мы видим, наиболее крутой переход без осцилляций получается при значении L1 равном 4 мкГн. Изменим это значение в схеме и отобразим получившуюся АЧХ на рисунке 8. Файл – LFF 3 (Smooth).cir.

Рисунок 8. АЧХ с C3 при L1=4u
3. Теперь определим полосу пропускания получившегося фильтра. Результат покажем на рисунке 9.
|


Рисунок 9. Полоса пропускания ФНЧ
При значении емкости C3 равной 1 мкФ, мы получили частоту среза равную 50 кГц. Полученная частота велика для ФНЧ, поэтому уменьшим ее, до 500 Гц (см. пункт 1.2), что является, например, низкой частотой звукового диапазона частот.
Т.к. XC = -  , то при увеличении C, XC будет уменьшаться, и напряжение на C3 тоже уменьшится. Это приведет к уменьшению (сдвигу влево) полосы пропускания.
, то при увеличении C, XC будет уменьшаться, и напряжение на C3 тоже уменьшится. Это приведет к уменьшению (сдвигу влево) полосы пропускания.
Подберем необходимое значение C3 в режиме степпинга. Результат подбора покажем на рисунке 10.

Рисунок 10. Подбор C3 для достижения полосы пропускания в 500 Гц
Из рисунка 10 видно, что необходимое значение находится где-то в диапазоне 100-110 мкФ. Для более точного подбора, попробуем изменять C3 в этом диапазоне, и рассмотрим АЧХ только в этой области. Результат покажем на рисунке 11.

Рисунок 11. Более точный подбор C3 для полосы пропускания 500 Гц
Из рисунка 11 видно, что необходимо значение C3 – 106 мкФ. Изменим это значение в схеме и покажем результат на рисунке 12. Файл – LFF 4 (Freq Band).cir.
|


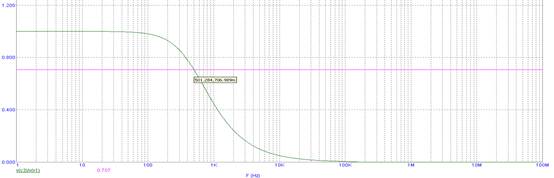
Рисунок 12. АЧХ ФНЧ с полосой пропускания 500 ± 50 Гц
Как мы видим, переход на АЧХ стал менее крутым, поэтому мы подберем в режиме степпинга значение индуктивности L2, для увеличения крутизны перехода. Из анализа в режиме степпинга (аналогично методу, описанному выше), мы видим, что необходимое значение L2 – 500 мкГн. Изменим номинал в схеме и покажем результирующую АЧХ на рисунке 13. Файл – LFF 5 (Freq Band Smooth).cir.
|

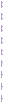
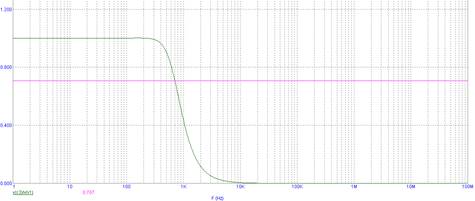
Рисунок 13. АЧХ с более крутым переходом
Как мы видим, немного изменилась полоса пропускания. Попробуем ее уменьшить до 500 Гц, сохранив крутизну перехода АЧХ. Для этого увеличим С3 и L2. Результат – на рисунках 14 и 15. Файл – LFF 6 (Freq Band Correct).cir.
|



Рисунок 14. АЧХ с полосой пропускания 500 Гц, при C3=150u, L2=700u

Рисунок 15. Схема с верной полосой пропускания и крутым переходом АЧХ
Температурный анализ
Дано:
1. Схема (источник, R, C, L)
2. Номиналы (см. рисунок 15)
3. Температурные коэффициенты R, C, L = 0.001
Необходимо:
Рассчитать коэффициент влияния температуры на изменение полосы пропускания
Решение:
Зададим температурные коэффициенты для моделей R, C и L. Вид окна параметров элемента, где указывается температурный коэффициент (например, для модели резистора), покажем на рисунке 16.


Рисунок 16. Задание температурного коэффициента для модели резистора
Определим коэффициент влияния температуры на изменение полосы пропускания, задав в окне AC Analysis предел изменения температур от -40 Cº до 40 Cº (с шагом изменения 20 Cº), и покажем результаты на рисунках 17 и 18. Файл – LFF 7 (Freq Temp).cir.

Рисунок 17. Вид окна AC Analysis
|
|

|


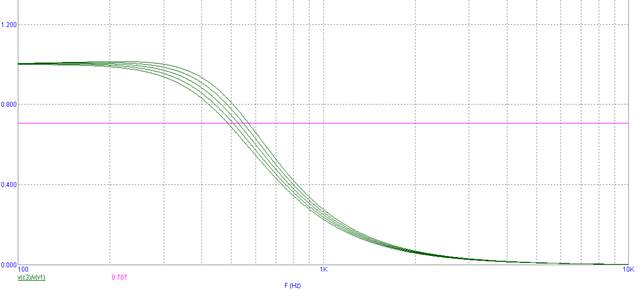
Рисунок 18. Изменение полосы пропускания под действием температуры
40 Сº=485 ± 5 Гц
20 Сº=505 ± 5 Гц
27 Сº=500 ± 5 Гц
αПП =  = 0,002
= 0,002
Статистический анализ
Прямая задача
Дано:
1. Схема (источник, R, C, L)
2. Номиналы (см. рисунок 15)
3. Допуски для элементов ΔR=20%, ΔC=30%, ΔL=25%
4. Вид закона распределения отклонения внутренних параметров от номинального значения (гауссовский, равномерный, наихудший случай)
Необходимо:
1. Найти среднее значение полосы пропускания
2. Получить δ (среднее квадратичное отклонение) разброса значений полосы пропускания от ее среднего значения
3. Построить гистограмму распределения значений полосы пропускания
Решение:
Для начала, зададим допуски моделей R, C и L, и покажем вид окна параметров элемента, где указывается допуски (например, для модели резистора), на рисунке 19. Файл – LFF 8 (Freq Common Stat).cir.


Рисунок 19. Задание допуска для модели резистора
На рисунке 20 покажем, как изменяется полоса пропускания при изменении значений элементов в пределах их допусков (для гауссовского).
|
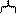


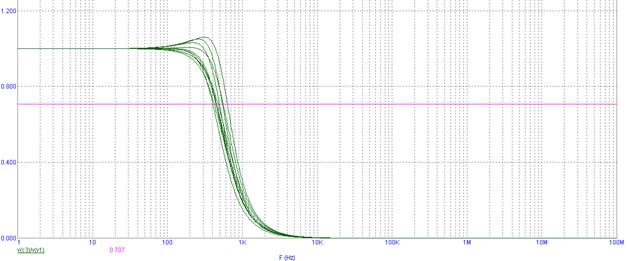
Рисунок 20. Пример изменения полосы пропускания
Теперь проведем статистический анализ с использованием метода Монте-Карло для разных законов распределения:
1. Гауссовский
| Число итераций | ||||||
| Среднее значение | 487,716 | 510,428 | 517,235 | 499,822 | 499,915 | 502,555 |
| δ | 66,523 | 57,425 | 61,89 | 62,116 | 63,607 | 62,163 |
Минимальное число итераций – 500
· Среднее значение = 499 Гц
· δ = 62 Гц
· Гистограмма распределения значений полосы пропускания показана на рисунке 21 (для 1000 итераций).

Рисунок 21. Гистограмма для гауссовского закона распределения
2. Равномерный
| Число итераций | |||
| Среднее значение | 506,966 | 509,647 | 509,292 |
| δ | 89,54 | 91,752 | 92,706 |
· Среднее значение = 509 Гц
· δ = 91 Гц
· Гистограмма распределения показана на рисунке 22 (для 1000 итераций).

Рисунок 22. Гистограмма для равномерного закона распределения
3. Наихудший случай
| Число итераций | |||
| Среднее значение | 529,296 | 528,682 | 529,949 |
| δ | 175,703 | 166,101 | 164,106 |
· Среднее значение = 529 Гц
· δ = 166 Гц
· Гистограмма распределения показана на рисунке 23 (для 1000 итераций).

Рисунок 23. Гистограмма для закона распределения на наихудший случай
Обратная задача
Дано:
1. Схема (источник, R, C, L)
2. Номиналы (см. рисунок 15)
3. Вид закона распределения отклонения внутренних параметров от номинального значения (гауссовский, равномерный, наихудший случай)
4. δПП выходной характеристики от номинального значения (см. пункт 1.2)
Определить:
Допуски элементов, обеспечивающих это отклонение
По ТЗ: δТЗ (ПП) = 50 Гц (см. пункт 1.2)
Алгоритм:
1. Устанавливаем допуски ∆R, ∆C, ∆L
2. Находим δРАС. Если δРАС<=δТЗ – оставляем выбранные допуски, если δРАС>δТЗ, продолжаем подбирать допуски методом Stepping’а (при отключенном методе Монте-Карло).
Определяем, какой из элементов много больше влияет на полосу пропускания, и уменьшаем его допуск.
Для того, чтобы определить, какой же элемент влияет больше, мы строим несколько графиков для каждого элемента, изменяя значение элемента в пределах погрешности и на графике находим ∆fПП ∆R, ∆fПП ∆С, ∆fПП ∆L.
Подбор допусков по шагам:
1. δТЗ (ПП)=50 Гц, δРАС=62,032 Гц, ∆R=20%, ∆C=30%, ∆L=25%
δРАС>δТЗ
Для R3: RН=1 Ом, RН-∆=0,8 Ом, RН+∆=1,2 Ом. Влияние изменения значений R3 в пределах допуска на изменение полосы пропускания, покажем на рисунке 24.
|
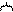
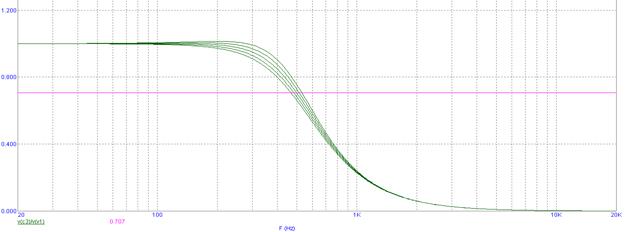
Рисунок 24. Коэффициент влияния R3 на изменение полосы пропускания
Для C3: CН=150 мкФ, СН-∆=105 мкФ, СН+∆=195 мкФ. Влияние изменения значений C3 в пределах допуска на изменение полосы пропускания, покажем на рисунке 25.

|
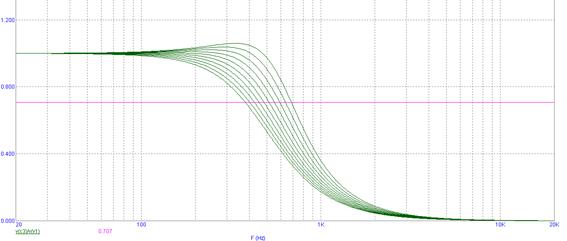
Рисунок 25. Коэффициент влияния C3 на изменение полосы пропускания
Для L2: LН=700 мкГн, LН-∆=525 мкГн, LН+∆=875 мкГн. Влияние изменения значений L2 в пределах допуска на изменение полосы пропускания, покажем на рисунке 26.
|
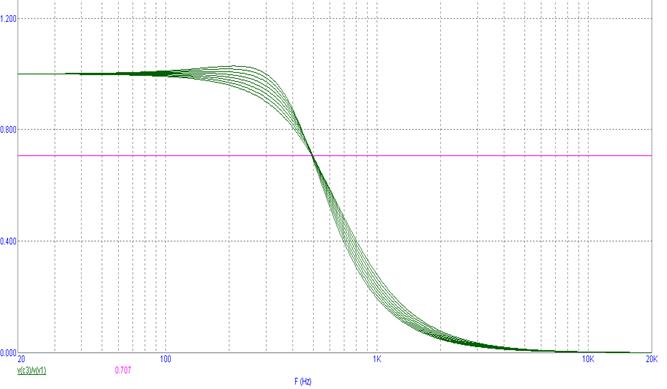
Рисунок 26. Коэффициент влияния L2 на изменение полосы пропускания
∆fПП ∆C >> ∆fПП ∆R >>∆fПП ∆L, поэтому уменьшаем ∆C с 30% до 20%
2. δТЗ (ПП)=50 Гц, δРАС=38,909 Гц, ∆R=20%, ∆C=20%, ∆L=25%
δРАС<δТЗ
На этом подбор допусков заканчиваем: ∆R=20%, ∆C=20%, ∆L=25%. Файл – LFF 9 (Freq Reverse Stat).cir.