Характер последовательностей, формируемых реальным источником сообщений, зависит от существующих ограничений на выбор знаков. Они выражаются в том, что вероятности реализации знаков различны и между ними существуют корреляционные связи. Эти ограничения приводят к тому, что вероятности формируемых последовательностей существенно различаются.
Пусть, например, эргодический источник без памяти последовательно выдает знаки  в соответствии с вероятностями 0,1; 0,3; 0,6. Тогда в образованной им достаточно длинной последовательности знаков мы ожидаем встретить в среднем на один знак
в соответствии с вероятностями 0,1; 0,3; 0,6. Тогда в образованной им достаточно длинной последовательности знаков мы ожидаем встретить в среднем на один знак 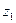 три знака
три знака 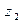 и шесть знаков
и шесть знаков 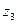 . Однако при ограниченном числе знаков в последовательности существуют вероятности того, что она будет содержать;
. Однако при ограниченном числе знаков в последовательности существуют вероятности того, что она будет содержать;
только знаки 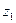 (либо
(либо 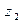 , либо
, либо 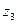 );
);
только знаки 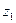 и один знак
и один знак 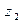 или
или 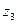 ;
;
только знаки 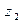 и один знак
и один знак 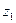 или
или 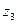 ;
;
только знаки 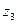 и один знак
и один знак 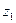 или
или 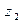 ;
;
только знаки 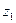 и два знака
и два знака 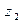 или
или 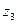 и т. д.
и т. д.
С увеличением числа знаков вероятности появления таких последовательностей уменьшаются.
Фундаментальные свойства длинных последовательностей знаков, создаваемых эргодическим источником сообщений, отражает следующая теорема, имеющая фундаментальное значение в теории информации.
Теорема 1. Как бы ни малы были два числа e > 0 и d > 0 при достаточно большом М, все последовательности могут быть разбиты на две группы.
Одну группу составляет подавляющее большинство последовательностей, каждая из которых имеет настолько ничтожную вероятность, что даже суммарная вероятность всех таких последовательностей очень мала и при достаточно большом М будет меньше сколь угодно малого числа e. Эти последовательности называют нетипичными. Говорят, также, что такие последовательности относятся к «маловероятной» группе реализаций.
Вторая группа включает типичные последовательности («высоковероятная» группа реализаций), которые при достаточно большом М отличаются тем, что вероятности их появления практически одинаковы, причем вероятность р любой такой последовательности удовлетворяет неравенству
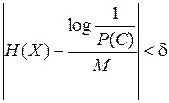 , (6.11)
, (6.11)
где Н (Х)– энтропия эргодического источника, определяемая по (6.10).
Соотношение (6.11) называют также свойством асимптотической равномерности длинных последовательностей. Рассмотрим его подробнее.
Из данной теоремы следует, что для всех типичных последовательностей
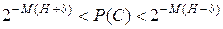 .
.
При М → ∞ δ → 0. Поэтому при достаточно большом М можно положить
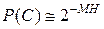 . (6.12)
. (6.12)
Из (6.12) видно, что все последовательности С равновероятны и число их равно
NT ≈ 1/ p (C) или NT ≈2 МН (Х). (6.12а)
Поскольку при М ® ¥ источник сообщений с вероятностью, сколь угодно близкой к единице, выдает только типичные последовательности, неопределенность создания каждой такой последовательности с учетом их равновероятности составляет  . Тогда величина log(1/ p)/ M представляет собой неопределенность, приходящуюся в среднем на один знак. Конечно, эта величина практически не должна отличаться от энтропии источника, что и констатируется соотношением (6.11).
. Тогда величина log(1/ p)/ M представляет собой неопределенность, приходящуюся в среднем на один знак. Конечно, эта величина практически не должна отличаться от энтропии источника, что и констатируется соотношением (6.11).
Ограничимся доказательством теоремы для простейшего случая эргодического источника без памяти. Оно непосредственно вытекает из закона больших чисел, в соответствии с которым в длинной последовательности из М элементов алфавита l 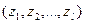 ,имеющих вероятности появления
,имеющих вероятности появления 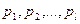 ,содержится Мр 1элементов
,содержится Мр 1элементов 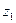 , Мр 2элементов
, Мр 2элементов 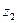 и т.д.
и т.д.
Тогда вероятность р реализации любой типичной последовательности близка к величине
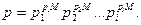 (6.13)
(6.13)
Логарифмируя правую и левую части выражения (6.13), получаем

откуда (при очень больших M)
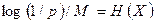 .
.
Для общего случая теорема доказывается с привлечением цепей Маркова.
Покажем теперь, что за исключением случая равновероятного и независимого выбора букв источником, когда нетипичные последовательности отсутствуют, типичные последовательности при достаточно большом N составляют незначительную долю от общего числа возможных последовательностей.
Общее число всевозможных последовательностей длины М, вырабатываемых источником,
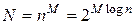 .
.
 ,
,
откуда при М → ∞ NT/N → 0, так как Н (Х) – log п ≤ 0. Однако хотя типичных последовательностей мало, но только они в основном вырабатываются источником, как то следует из теоремы.
Пусть, например,
а = 2, п = 100, Н = 2,75, т = 8. Тогда N = 8100 = 2300, N 2 = 2100 ּ 2,75 = 2275.
Отсюда 
Т.е. к высоковероятной группе относится лишь одна тридцатимиллионная доля всех реализаций.
К.Шеннон показал, что рассмотренные свойства длинных последовательностей могут служить основанием для осуществления эффективного кодирования информации.
Целесообразно отметить, что в простейшем случае отсутствия статистической зависимости между элементами процесса свойство Е является простым следствием закона больших чисел [7].