Основные положения
Сила взаимодействия двух тел с шероховатыми поверхностями включает две составляющие: нормальную 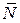 , перпендикулярную поверхности контакта, и силу трения
, перпендикулярную поверхности контакта, и силу трения 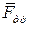 , лежащую в плоскости контакта тел (рис. 15).
, лежащую в плоскости контакта тел (рис. 15).
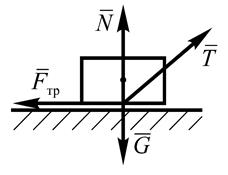 Рис. 15 Рис. 15
| Cила трения препятствует скольжению одного тела по поверхности другого и направляется всегда в сторону, противоположную возможному относительному смещению взаимодействующих точек соприкасающихся тел. Поэтому для нахождения направления силы трения необходимо мысленно представить, куда будет двигаться тело при отсутствии силы трения, а затем направить вектор силы трения в сторону, противоположную этому возможному движению. |
В соответствии с законом Кулона максимальное значение силы трения пропорционально нормальной силе взаимодействия между телами:
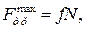
где 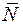 - сила нормального давления, прижимающая тела друг к другу. Безразмерный коэффициент f называется коэффициентом трения скольжения. Его значение определяется физическими свойствами материалов тел и размерами неровностей их поверхностей, но не зависит от площади соприкосновения тел.
- сила нормального давления, прижимающая тела друг к другу. Безразмерный коэффициент f называется коэффициентом трения скольжения. Его значение определяется физическими свойствами материалов тел и размерами неровностей их поверхностей, но не зависит от площади соприкосновения тел.
Значение силы трения равно произведению коэффициента трения на силу нормальной реакции только в том случае, если заранее известно, что при бесконечно малом изменении приложенных активных сил начнется движение тела. В общем же случае значение силы трения определяется неравенством: 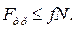
При условии 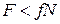 силу трения называют силой сцепления (
силу трения называют силой сцепления (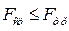 ).
).
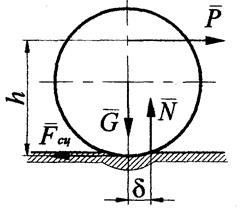 Рис. 16
Рис. 16
| Трение качения возникает при перекатывании тела (катка) по поверхности другого тела и обусловлена их деформацией. Вследствие этого тела соприкасаются по некоторой площадке, а нормальная составляющая 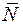 полной реакции опорной поверхности смещается от оси катка в сторону его движения. Величина смещения δ в предельном положении покоя называется коэффициентом трения качения и имеет размерность длины. Сила полной реакции опорной поверхности смещается от оси катка в сторону его движения. Величина смещения δ в предельном положении покоя называется коэффициентом трения качения и имеет размерность длины. Сила 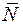 и вес катка и вес катка 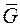 образуют пару сил с плечом δ, момент которой образуют пару сил с плечом δ, момент которой 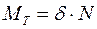 называется моментом трения качения. называется моментом трения качения.
|
Качение катка без скольжения будет иметь место, если
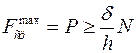 .
.
Методика решения задач на равновесие с учетом сил трения – такая же, как и при отсутствии трения. Однако в этом случае рассматривается предельное положение равновесия тела. Это позволяет по вышеприведенным зависимостям определить наибольшую силу трения покоя и момент трения и с учетом этого составить необходимые уравнения равновесия, соответствующие системе сил реакций и активных сил, действующих на тело.
Пример расчета
Для стержня, находящегося в равновесии, определить максимальное значение силы 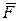 , при котором сохраняется равновесие. Найти для этого случая равнодействующие реакций опорных поверхностей.
, при котором сохраняется равновесие. Найти для этого случая равнодействующие реакций опорных поверхностей.
Дано:  Н;
Н; 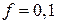 ;
; 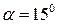 ;
; 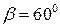 ;
; 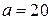 см;
см; 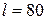 см.
см.
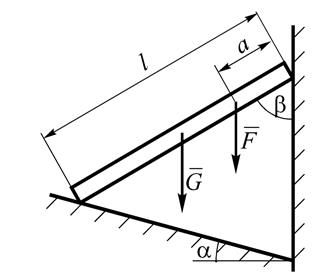
Рис. 16. Схема опирания стержня
Решение:
1. Изображаем стержень с наложенными на него механическими связями: активными силами, действующими на тело, являются сила тяжести 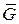 и сила
и сила 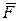 , стремящаяся привести его в движение. Препятствуют движению тела опоры в точках А и В. Их нормальные реакции
, стремящаяся привести его в движение. Препятствуют движению тела опоры в точках А и В. Их нормальные реакции 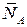 и
и 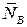 направлены перпендикулярно опорным плоскостям. При отсутствии трения стержень под действием сил
направлены перпендикулярно опорным плоскостям. При отсутствии трения стержень под действием сил 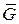 и
и 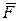 начнет перемещаться. Силы трения
начнет перемещаться. Силы трения 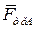 и
и 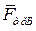 препятствуют этому его возможному движению (рис. 17).
препятствуют этому его возможному движению (рис. 17).
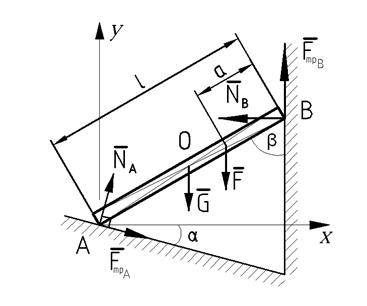
Рис. 17. Расчетная схема
2. Изображаем систему отсчета: ось Ах направляем горизонтально, ось Ау – перпендикулярно ей.
3. На тело действует система произвольно расположенных в плоскости сил, поэтому составляем три уравнения равновесия:
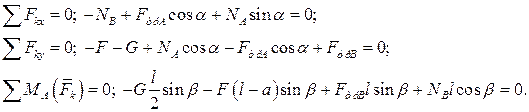 (13)
(13)
При максимальном значении силы 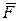 , соответствующем состоянию предельного равновесия тела, выполняются равенства:
, соответствующем состоянию предельного равновесия тела, выполняются равенства: 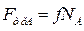 ,
, 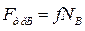 . Подставляя их в систему уравнений, после преобразований получим:
. Подставляя их в систему уравнений, после преобразований получим:

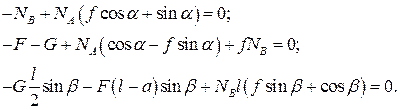
Подставляем числовые значения:
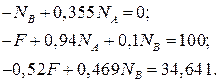
Таким образом, получена система трех уравнений с тремя неизвестными величинами: 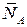 ,
, 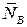 ,
, 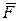 . Решаем ее:
. Решаем ее:
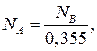
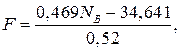
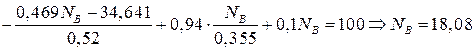 Н,
Н,
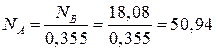 Н,
Н,
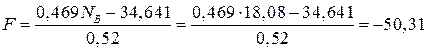 Н.
Н.
Знак «-» показывает, что при данных условиях задачи равновесие возможно лишь при силе 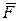 , направленной вверх (физически это связано с достаточно низким коэффициентом трения f).
, направленной вверх (физически это связано с достаточно низким коэффициентом трения f).
Действующие силы трения:
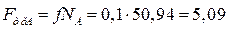 Н,
Н,
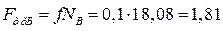 Н.
Н.
4. Определяем равнодействующие сил реакций опорных поверхностей. Поскольку силы 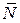 и
и 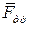 перпендикулярны, то их равнодействующую можно рассчитать, применяя теорему Пифагора. Тогда:
перпендикулярны, то их равнодействующую можно рассчитать, применяя теорему Пифагора. Тогда:
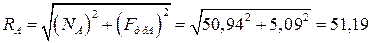 Н,
Н,
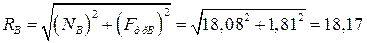 Н.
Н.
Замечание. При выполнении расчетно-графической работы для решения систем уравнений можно применить вычислительную технику. В этом случае не следует подробно описывать ход решения системы, но к работе необходимо приложить распечатку исходных уравнений и результатов расчета.
Решение системы уравнений методом Крамера в Mathcad:
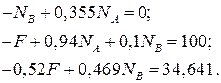 Определяем матрицу системы А и матрицу правой части В:
Определяем матрицу системы А и матрицу правой части В:
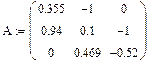
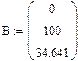 Вычислим определитель матрицы системы А:
Вычислим определитель матрицы системы А:
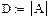
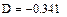 Определитель отличен от нуля, система имеет единственное решение.
Вычисление решения по формулам Крамера:
Определитель отличен от нуля, система имеет единственное решение.
Вычисление решения по формулам Крамера:
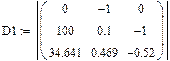 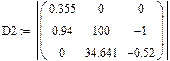 
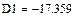 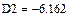 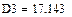
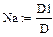 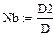 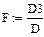
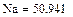 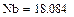 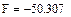
|
Ответ: 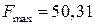 Н,
Н, 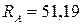 Н,
Н, 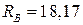 Н.
Н.
ЦЕНТР ТЯЖЕСТИ