Лабораторная работа №5
Определение фокусных
Расстояний линз.
Определение фокусных расстояний линз.
Цель работы: экспериментальное определение фокусных расстояний тонких линз.
Принадлежности: оптическая скамья, двояковогнутая и двояковыпуклая линзы, экран, светящийся предмет, линейка.
Оптическая система называется идеальной, если в ней сохраняется гомоцентричность пучка и изображение получается строго геометрически подобно предмету. Гомоцентрически пучок, имеющий центр, т.е. все лучи или их продолжения выходят из одной точки или сходятся в одной точке. Идеальная оптическая система обладает осью симметрии, которая называется главной оптической осью. Лучи параллельные главной оптической оси, проходят через идеальную оптическую систему, пересекаются в одной точке, называется фокусом оптической системы. Всякая оптическая система имеет два фокуса. В тонкой линзе за фокусное расстояние можно принять расстояние от фокуса до линзы, по главной оптической оси. Лучи, проходящие через фокусы линзы, и оптический центр, удобно использовать для построения изображения в линзах.
Экспериментальное определение фокусных расстояний линзы основано на измерении расстояний от предмета до линзы, от изображения до линзы, комбинации этих расстояний согласно формуле линзы:
(1)
где а1 – расстояние от предмета до линзы,
а2 – расстояние от линзы до изображения,
f – фокусное расстояние.
В формуле (1) все расстояния являются алгебраическими величинами. При расчете по формуле (1) необходимо пользоваться следующими правилами знаков: 1) расстояния отсчитываются от оптического центра линзы Р (рис.1), 2)отрезки которые откладываются против хода луча, записываются со знаком ''+'', 3) численные значения фокусного расстояния подставляют со знаком ''+'', если линза имеет положительную оптическую силу, для линзы с отрицательной оптической силой- подставляется ''-''.
Отношение линейных размеров изображения (L) и предмета (1) называется увеличением линзы:
(2)
Для собирающей линзы имеем:
где (-а1)=а, а2=в.
Здесь а и в арифметические величины. В нашем эксперименте l =1,5см (сторона предмета).
Рис.1
Опыт 1. Определение фокусного расстояния двояковыпуклой линзы по расстоянию от предмета до линзы и от линзы до изображения.
Из формулы (2) имеем:
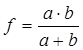
Ввиду неточности визуальной оценки резкости изображения, измерения нужно проводить не менее трех раз. Часть измерений нужно провести при увеличенном, а часть при уменьшенном изображении.
Опыт 2. Определение фокусного расстояния по величине предмета, по величине его изображения L и расстояния от линзы до изображения.
Комбинируя формулу (2) получим:
Эта формула является рабочей формулой для этого эксперимента. Все три измерения в данном опыте нужно проводить при увеличенном изображении.
Опыт 3. Определение фокусного расстояния положительной линзы по способу Бресселя.
Если расстояние от предмета до изображения, которое обозначим через А, более 4f, то всегда найдется два таких положения линзы, при которых на экране получится отчетливое изображение предмета: в одном случае уменьшенное, а в другом – увеличенное (рис.2).
Воспользовавшись уравнением (2), можно записать для первого и второго положения линзы:
Приравнивая правые части этих уравнений, найдем: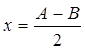 
Чтобы получить выражение для фокусного расстояния, рассмотрим одно из положений линзы, например:
для него расстояние от предмета до линзы: 
а расстояние от линзы до изображения: 
Подставляя эти величины в формулу (1), найдем:
|
(3)
Для проведения эксперимента предмет и экран установить на расстоянии А > 4f. Грубое значение будет из предыдущих опытов. Передвигая линзу между предметом и экраном, находят положения линзы, при которых получается увеличенное и уменьшенное изображения предмета. По шкале на оптической скамье проводят необходимые измерения. По среднему значению В, используя формулу (3), вычисляют фокусное расстояние. Измерения проводят для трех различных А.
Опыт 4. Определение фокусного расстояния рассеивающей линзы.
Изображение реального объекта в рассеивающей линзе является мнимым и поэтому не может быть получено на экране непосредственно. Для определения фокусного расстояния рассеивающей линзы удобно воспользоваться мнимым источником, создаваемым собирающей линзой. Такое расположение линз показано на рис.3.
(4)
где а – расстояние между точками Д и С, b - расстояние СЕ.
Для проведения измерений на оптической скамье размещают осветитель, собирающую линзу и экран. Передвигая экран, получают на нем отчетливое изображение предмета. Записав отчет этого положения экрана по оптической скамье, сдвигают экран и вновь находят изображение предмета. Таких установок и отчетов делают не менее трех раз и берут из них среднее арифметическое. Это дает положение точки Д. Отодвинув экран вправо, ставят на скамью между найденным выше положением экрана (точки Д) и собирающей линзой исследуемую линзу и вновь находят отчетливое изображение предмета. Отсчитывают по шкале оптической скамьи положение линзы и, двигая ее, повторяют установку и отсчеты до трех раз, оставляя неподвижным экран. Из полученных результатов берут среднее. Это дает положение точки С. Вычислив расстояния СЕ и ДС, по формуле (4) находят фокусное расстояние.
Рис.3