Расширенный метод Хюккеля

Лекция №27. Метод Молекулярных Орбиталей Хюккеля.

Этот чрезвычайно простой не-ССП метод, первоначально предложенный для углеводородов (Хюккель, 1931), основан на нескольких очень сильных приближениях:

1. Принимается p -электронное приближение; считают, что АО образуют ортонормальный базис, т.е. S _mn = d_mn.

2. Межэлектронными взаимодействиями (т.е. всеми двух-электронными кулоновскими и обменными интегралами) пренебрегают. Из-за этого решение уравнений метода не требует итераций и проводится в один шаг.

3. Матричные элементы оператора Фока оцениваются на основании эмпирической информации и являются фиксированными:

h_mm = a_m,

h_mn = kb_mn. (1)

a_m называется кулоновским интегралом (его не следует путать с двухэлектронными кулоновскими интегралами g_AB), он принимается равным потенциалу ионизации электрона на орбитали m в свободном атоме.

4. Принимается, что b_mn =0, если АО m и n не принадлежат ковалентно связанным атомам.

Соответствующие этим приближениям уравнения Рутана имеют вид

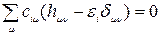(2)

и называются уравнениями Хюккеля, имеющими ненулевые решения при равенстве нулю детерминанта

|h_mn - e _i d_mn | = 0. (3)

Полная энергия в этом методе есть просто сумма орбитальных энергий

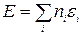, n=0, 1 или 2, (4)

где n – число электронов на МО.

Уравнения Хюккеля могут быть легко записаны и решены для любой системы. Рассмотрим пример молекулы этилена С₂Н₄, имеющей 2p -электрона (свяжем их с c (р_z) -АО атомов углерода, направленными перпендикулярно плоскости молекулы). Интегралы a_С = -11,0 эВ, b_СС –2,4 эВ. Детерминант (3) имеет вид

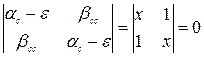(5)

(здесь введены обозначения х=(a_С - e)/b_СС). Раскрывая определитель, имеем:

х² –1=0 и х = ± 1, т.е. e ₁= a_С +b_СС, e₂ =a_С - b_СС.

В принятых обозначениях система уравнений (2) имеет вид

с₁ х + с₂ = 0

с₁ + с₂ х = 0, (6)

Подставим теперь х = ± 1 в (6). При х= -1 имеем с₁ = с₂ . Используя условие нормировки волновой функции этилена с₁² + с₂² = 1, получаем с₁ = с₂ = 1/Ö 2. Таким образом, одна из p -МО этилена имеет вид

j₁ = 1/Ö 2 (c₁ +c₂). (7)

При х = 1 имеем с₁ = - с₂ и, повторяя рассуждения, получаем другую p -МО.

j₂ = 1/Ö 2 (c₁ - c₂). (8)

Так как b_СС < 0, то e₁ < e₂ причем, e₁ - e₂ = 2b_СС. Это означает, что МО j₁ более энергетически стабильна.

Полинг, Уэлланд, Стрейтвизер, Дьюар и другие предложили различные модификации метода Хюккеля, распространив его, в частности, на системы с гетероатомами в цикле. Модификация, в основном, касалась способа выбора параметров a и b и подробно описана в литературе (М.Дьюар.«Метод молекулярных орбиталей в органической химии»).

Метод Хюккеля, безусловно, является лишь качественным: он ограничен предсказанием энергетики МО сопряженных систем и не способен дать информацию о молекулярной структуре. Однако за счет удачной параметризации этот метод может давать хорошие относительные орбитальные энергии для рядов p-электронных органических и металлоорганических систем. Это позволяет, в частности, идентифицировать полосы в электронных спектрах поглощения таких молекул, отождествляя разности орбитальных энергий e_k - e_i с энергиями переходов.

Расширенный метод Хюккеля

Наиболее радикальная модификация метода Хюккеля принадлежит Р.Хоффману (1963). Он предложил сохранить оригинальную схему Хюккеля, но включить в рассмотрение все валентные (а не только p) орбитали и явно учесть интегралы перекрывания. В итоге уравнения метода, получившего название расширенный метод Хюккеля (РМХ), формально совпадают с уравнениями Рутана, однако содержание матричных элементов совершенно иное. Матричные элементы оператора Фока F_mn º h_mn являются параметрами или оцениваются с помощью соотношений, включающих эти параметры. Наиболее часто используются следующие оценки:

h_mm = - I_m.,

h_mn = 0.5K(h_mm + h_nn). (9)

В варианте Вольфсберга-Гельмгольца К=1,75. Интегралы перекрывания вычисляются аналитически.

Энергия молекулы с закрытой оболочкой в методе РМХ является удвоенной суммой энергий занятых МО и описывается выражением

Е= 2(å åс ²_{i m} h_mm + å å å с_{i m} с _{i n} h_mn), (10)

в котором члены, ответственные за межэлектронное и межъядерное взаимодействие, не учитываются. В системах с равномерным распределением электронов выражение (10) дает хорошие относительныеоценки энергии в рядах соединений. Гетероатомы нарушают равномерность электронного распределения и РМХ здесь часто непригоден. Тем не менее расширенный метод Хюккеля дает зачастую лучшие результаты, чем его простой аналог, при изучении конформаций циклических молекул, барьеров внутреннего вращения, относительный порядок уровней энергии.

Уместно отметить роль, которую РМХ сыграл в развитии химии. Именно с его помощью было установлен механизм связывания в металлоценах, сфомулировано правило Вудворда-Хоффмана, исследованы свойства основных состояний многих алифатических и ароматических систем и др.