Построить дерево поиска с элементами – символами. Используя операции Locate, Father, Value и Delete, найти узел, являющийся отцом узла с заданным значением, вывести значение найденного узла и исключить его из дерева. Вывести дерево с помощью отступов, результаты его обхода слева направо и число узлов дерева (до и после исключения узла). Класс дерева поиска содержатся в модуле BinTrees.
// Лабораторная работа 3. Бинарные деревья.
// Выполнил Сергеев Андрей, группа 500.
// Работа с деревом поиска.
// Исходные данные - элементы дерева - в файле LW3Dat.txt
// Результаты работы помещаются в файл LW3Res.txt
program LW3;
{$APPTYPE CONSOLE}
uses SysUtils, BinTrees in 'BinTrees.pas';
Var
SearchTree: tSearchTree; // динамический экземпляр дерева поиска
fDat, fRes: Text; // файлы исходных данных и результатов
Item, FathItem: pItem; // указатели на узел дерева и на отца узла
v: tValue; // значение узла дерева
Begin
Try
Assign(fDat, ‘LW3Dat.txt'); Reset(fDat);
Assign(fRes,'LW3Res.txt'); Rewrite(fRes);
// создание экземпляра SearchTree класса tSearchTree
SearchTree:= tSearchTree.Create;
SearchTree.Build(fDat); // построение дерева поиска
WriteLn(fRes, 'Работа с деревом поиска');
WriteLn(fRes, 'Поиск и удаление отца заданного элемента дерева');
WriteLn(fRes, 'Построено дерево с числом узлов ',SearchTree.Size,':');
SearchTree.WriteTo(fRes); // вывод исходного дерева поиска
Write(fRes, 'Обход дерева слева направо:');
SearchTree.LeftRightRevision(fRes); // обход дерева слева направо
Write(WinDos('Для какого элемента нужно найти отца?'));
ReadLn(v);
WriteLn(fRes, 'Нужно найти отца для элемента ', v);
Item:= SearchTree.Addr(v); // поиск узла со значением v
if Item= nil
then WriteLn(fRes,'Элемента с ключом ',v,' в дереве нет.')
Else begin
FathItem:= SearchTree.Father(Item); // адрес отца узла со значением v
if FathItem= nil
then WriteLn(fRes,'Заданный элемент не имеет отца.')
else begin // если у заданного элемента есть отец
v:= SearchTree.Value(FathItem);
WriteLn(fRes, 'Значение отца заданного элемента = ', v);
SearchTree.Delete(v); // исключение отца узла
WriteLn(fRes,'Состояние дерева после исключения:');
SearchTree.WriteTo(fRes); // вывод дерева поиска после исключения
WriteLn(fRes, 'Обход дерева слева направо:');
SearchTree.LeftRightRevision(fRes); // обход дерева поиска слева направо
WriteLn(fRes,'Число узлов дерева:', SearchTree.Size);
end;
end;
SearchTree.Free;
Finally
Close(fDat); Close(fRes);
end;
end.
 Тема 4. Графы
Тема 4. Графы
1. Основные понятия и определения
Граф состоит из множества узлов и множества дуг. Каждая дуга в графе указывается парой узлов. Примеры графов:
Граф G 1 Граф G 2
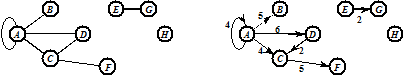
Для графа G 1 множество узлов – { A, B, C, D, E, F, G, H }, множество дуг – {(A, B), (A, D), (A, C), (C, D), (C, F), (E, G), (A, A)}. Дуга, соединяющая узел с самим собой, называется петлей. Узел может не иметь связанных с ним дуг (узел H графа G 2). Если пары узлов, образующих дугу, упорядочены, то граф называют ориентированным, или направленным, графом (граф G 2 – ориентированный); дуги в этом случае изображают стрелками. В этой теме мы будем рассматривать только ориентированные графы без петель.
Узел n называется инцидентным дуге x, если n – это один из двух узлов упорядоченной пары, составляющей дугу x (говорят также, что дуга x инцидентна узлу n). Степень узла – это число дуг, инцидентных узлу. Полустепень захода узла – это число дуг, входящих в узел, а полустепень исхода узла – это число дуг, выходящих из узла. Например, узел C графа G 2 имеет полустепень захода 2, полустепень исхода 1 и степень 3. Узел n называется смежным с узлом m, если существует дуга из m в n.
Часть графа – это граф, содержащий часть узлов исходного графа и часть (любую) его дуг.
Подграфом графа называется такая его часть, которая вместе со всякой парой узлов содержит и дугу, если она есть в исходном графе.
Суграф содержит все узлы исходного графа и часть его дуг.