Федеральное агентство по образованию
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
Рязанский государственный радиотехнический университет
СТРУКТУРЫИ АЛГОРИТМЫ
ОБРАБОТКИ ДАННЫХ
Динамические структуры данных
Методические указания
Рязань 2010
Содержание
Введение 4
1. Терминология. 4
2. Классификация структур данных по различным признакам.. 5
3. Типовые операции над структурами данных. 6
4. Эффективность алгоритмов. O-обозначения. 6
Тема 1. Стеки, очереди, деки.. 8
1. Стек. 8
2. Операции над стеком.. 8
3. Реализация стека. 8
4. Реализация основных операций над стеком.. 10
5. Использование стека для преобразования форм записи выражений. 11
6. Очередь. 12
7. Операции над очередью.. 13
8. Дек. 13
9. Операции над деком.. 14
10. Реализация очереди и дека. 14
11. Реализация основных операций над очередью и деком.. 14
12. Итератор. 17
Лабораторная работа 1. Стеки, очереди, деки. 18
Тема 2. Односвязные и двусвязные линейные списки.. 23
1. Линейный список. 23
2. Операции над линейным списком.. 23
3. Реализация линейного списка
в виде односвязной динамической структуры.. 24
4. Реализация основных операций над односвязным списком.. 24
5. Циклический список. 28
6. Операции над циклическим списком.. 28
7. Односвязная реализация циклического списка. 28
8. Реализация основных операций
над односвязным циклическим списком.. 30
9. Реализация линейного списка
в виде двусвязной динамической структуры.. 32
10. Реализация основных операций над двусвязным списком.. 34
11. Циклический двусвязный список. 36
12. Реализация основных операций
над двусвязным циклическим списком.. 37
Лабораторная работа 2. Односвязные и двусвязные линейные списки. 38
Тема 3. Бинарные деревья.. 43
1. Основные понятия и определения. 43
2. Построение бинарного дерева. 44
3. Операции над бинарным деревом.. 45
4. Реализация бинарного дерева. 47
5. Реализация основных операций над бинарным деревом.. 48
6. Дерево выражения. 51
7. Дерево поиска. 53
8. Операции над деревом поиска. 53
9. Реализация дерева поиска. 54
10. Реализация операций над деревом поиска. 54
11. Сбалансированные деревья. 57
12. Включение в сбалансированное дерево. 58
Лабораторная работа 3. Бинарные деревья. 64
Тема 4. Графы... 68
1. Основные понятия и определения. 68
2. Операции над графом.. 70
3. Реализация графа. 71
4. Реализация основных операций над ориентированным графом.. 73
5. Обход ориентированного графа. 78
6. Вычисление расстояния между узлами ориентированного графа. 80
Лабораторная работа 4. Ориентированные графы.. 82
Библиографический список 85
Введение
1. 
Терминология
Основной сферой применения ЭВМ являются обработка больших массивов информации (данных), организация их хранения, поиск в них нужных сведений. От правильной организации данных существенно зависит эффективность работы с этими данными. Данные могут быть организованы многими различными способами; логическая или математическая модель организации данных называется структурой данных. Структура данных характеризуется ее логическим (абстрактным) и физическим (конкретным) представлениями, а также совокупностью операций над структурой. Структуры данных, реализованные в конкретном языке программирования, называются типами данных этого языка.
Логическая структура – совокупность элементов данных, между которыми существуют некоторые отношения. Элементами данных могут быть: данное некоторого типа (например, целое число, вещественное число, логическое значение и т.п.), множество данных одного типа, множество данных разных типов или структура данных.
Отношения между элементами данных могут быть различными. Например, в массиве элементы данных имеют один и тот же тип и строго упорядочены.
Физическая структура – способ представления данных в машинной памяти.
В общем случае между логической и физической структурами существует различие, степень которого зависит и от самой структуры, и от той физической среды, в которой она должна быть отражена. Пример – двумерный массив. Кроме того, могут существовать различные структуры хранения одной и той же структуры данных, созданные с целью более эффективного выполнения тех или иных операций над структурой данных. Пример – реализация списка на базе массива и цепочки динамических переменных.
Вследствие различия между логической и физической структурами в вычислительной системе должны существовать процедуры взаимного отображения этих структур. Причем каждая операция может рассматриваться применительно к логической или физической структуре. Например, доступ к элементу двумерного массива на логическом уровне реализуется указанием номеров строки и столбца; на физическом уровне доступ осуществляется с помощью функции адресации, которая при известном начальном адресе массива в машинной памяти преобразует номера строки и столбца в адрес соответствующего элемента массива.
2. Классификация структур данных по различным признакам
Всю совокупность данных можно разделить на две большие группы: данные статической структуры и данные динамической структуры.
Данные статической структуры характеризуются тем, что взаимное положение и взаимосвязь элементов структуры всегда остаются постоянными. Данные статической структуры могут быть простыми (скалярными) и составными, которые формируются из простых структур по какому-либо закону.
Данные динамической структуры – это данные, внутреннее строение которых формируется по какому-либо закону, но количество элементов, их взаиморасположение и взаимосвязи могут динамически изменяться во время выполнения программы согласно закону формирования. К данным динамической структуры относятся файлы, несвязанные и связанные динамические данные.
По различным признакам структуры данных можно классифицировать следующим образом.
v По отношению к месту хранения:
Ø оперативные структуры (во внутренней памяти);
Ø файловые структуры (во внешней памяти).
v По наличию связей между элементами данных:
Ø несвязные (векторы, массивы);
Ø связные (списковые структуры):
· односвязные (списки);
· двусвязные (списки, бинарные деревья);
· многосвязные (деревья, графы).
v По признаку изменчивости (возможность изменения числа элементов и связей между ними):
Ø статические (векторы, массивы);
Ø полустатические (стеки, очереди, реализованные с помощью статических физических структур);
Ø динамические (стеки, очереди, реализованные с помощью динамических физических структур, списки).
v По признаку упорядоченности элементов структуры:
Ø линейные (массивы, стеки, очереди, списки);
Ø нелинейные (деревья, графы).
3. Типовые операции над структурами данных
1. Операция «создать» создает соответствующую структуру данных. Например, в Паскале переменная и массив могут быть созданы с помощью соответствующих операторов описания, что приводит к выделению адресного пространства для переменной и массива. Процедура New приводит к созданию переменной типа указателя.
2. Операция «уничтожить» приводит к уничтожению созданной структуры данных.
Например, в Паскале структуры данных, созданные внутри блока (процедуры), уничтожаются после выхода из этого блока. Процедура Dispose уничтожает переменную типа указателя.
3. Операция «выбрать» осуществляет доступ к данным внутри самой структуры. Выполнение этой операции зависит от структуры данных. Обращение, например, к переменной или элементу массива в операторе присваивания делает доступной соответствующую область памяти.
4. Операция «обновить» приводит к изменению данных в структуре.
4. Эффективность алгоритмов. O-обозначения
Эффективность алгоритмов зависит от двух факторов:
1) память, требуемая для реализации алгоритма на ПК;
2) время, необходимое для выполнения алгоритма.
Лучший способ сравнения эффективностей алгоритмов состоит в сопоставлении их порядков сложности. Порядок сложности алгоритма выражает его эффективность обычно через количество обрабатываемых данных. Порядок алгоритма – это функция, доминирующая над точным выражением временной сложности. Наиболее часто для выражения порядка сложности алгоритма используется так называемое О- обозначение. В этой нотации порядок сложности функции заключается в скобки, следующие за буквой «О ». О -функция выражает относительную скорость алгоритма в зависимости от некоторой переменной. Например, скорость работы алгоритма с временной сложностью O (n)падает пропорционально росту n. Существуют три важных правила для определения сложности:
1) постоянные множители не имеют значения для определения порядка сложности, т.е. O (k · f) = O (f);
2) порядок сложности произведения двух функций равен произведению их сложностей: О (f · g) = O (f)· O (g);
3) порядок сложности суммы функций равен порядку доминанты слагаемых, например: 
.
Приведем список функционального доминирования:
если N и L – переменные, a, b, c, d – константы, то
доминирует над 
;
доминирует над 
;
доминирует над 
, если a > b;
доминирует над 
, если а > 0;
доминирует над 
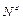, если c > d;
N доминирует над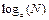 
, если a > 1.
Любой терм с одной переменной N не доминирует ни над каким термом с одной независимой переменной L.
Сложность алгоритма может быть определена исходя из анализа его управляющих структур. Алгоритмы без циклов и рекурсивных вызовов имеют константную сложность. Поэтому определение сложности алгоритма сводится в основном к анализу циклов и рекурсивных вызовов. Рассмотрим алгоритм удаления k -го элемента из массива размером n, состоящий из перемещения элементов массива от (k +1)-го до n -го на одну позицию назад к началу массива и уменьшения числа элементов n на единицу. Сложность цикла обработки массива составляет О (n – k), т.к. тело цикла (операция перемещения) выполняется n – k раз и сложность тела цикла равна О (1), т.е. является константой. Тип цикла (for, while, repeat) не влияет на сложность. Если один цикл вложен в другой и оба цикла зависят от размера одной и той же переменной, то вся конструкция характеризуется квадратичной сложностью. Вложенность повторений является основным фактором роста сложности. В качестве примера приведем сложность хорошо известных алгоритмов поиска и сортировки для массива размером n:
a) последовательный поиск: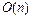 
;
b) бинарный поиск: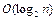 
;
c) пузырьковая сортировка: 
.
При изучении алгоритмов в последующих темах будут приведены оценки их сложности.
Тема 1. Стеки, очереди, деки
1. Стек
Стеком называется упорядоченный набор элементов, в котором включение новых элементов и исключение существующих выполняются только с одного конца, называемого вершиной стека. Каждый элемент стека характеризуется одним и тем же набором полей. Логическая структура стека:
| Включение Исключение | – • | E | D | C | B | A |
| — | ||||||
| Вершина |
Здесь A, B,... – элементы стека, каждый из которых может содержать одно или несколько полей. Стек функционирует по принципу LIFO (Last In – First Out – «последним пришел – первым исключается»). Известный пример стека – винтовочный патронный магазин. Число элементов стека не ограничено. Стек, в котором нет ни одного элемента, называется пустым.
Стековые структуры широко применяются в трансляторах при реализации вложенных подпрограмм, многоуровневых прерываний, рекурсивных процедур, для преобразования выражений из одной формы записи в другую.
2. Операции над стеком
Над стеком s могут быть выполнены следующие операции:
1) включение нового элемента со значением v в стек – Push (s,v);
2) исключение и возвращение значения верхнего элемента стека – Pop (s);
3) выработка признака «стек пуст» – Empty (s) (возвращает значение «истина», если стек пуст, и «ложь» – в противном случае);
4) считывание значения верхнего элемента без его исключения – TopValue (s);
5) возвращение числа элементов стека – Size (s);
6) очистка стека – Clear (s).
Первые три операции над стеками являются основными.
3. Реализация стека
Возможны два способа реализации стека – с помощью последовательного и связанного хранения элементов в памяти ЭВМ.
В первом случае базовой структурой для стека является массив. В памяти ЭВМ под стек отводится фиксированная область, достаточно большая, чтобы в ней можно было расположить некоторое максимальное число элементов. Указатель стека – адрес верхнего элемента стека в базовом массиве. При включении нового элемента в стек значение указателя увеличивается на размер элемента, затем в стек помещается информация о новом элементе. При исключении элемента прочитывается информация об исключаемом элементе, а затем значение указателя уменьшается на длину элемента стека. Изменения длины стека не должны выходить за пределы отведенной под него памяти.
Достоинством последовательного способа хранения элементов стека в памяти ЭВМ являются простота реализации стека и выполняемых над ним операций. Однако описание стека с помощью массива приводит к неэкономному использованию памяти ЭВМ – отведение фиксированного объема памяти при непостоянстве числа элементов стека. Невозможность увеличения однажды отведенного объема может вызвать переполнение стека, тогда как по определению число элементов стека не ограниченно.
Использование связанного хранения элементов стека в памяти ЭВМ позволяет избежать этих недостатков.
Реализация стека с помощью динамических переменных:
Каждый элемент стека состоит из двух частей: содержательной и ссылки на ранее включённый элемент. Переменная Head ссылочного типа указывает на верхний элемент стека (содержит адрес этого элемента). За первым включенным элементом стека (последним от Head) нет следующего элемента, поэтому в поле ссылки этого элемента записывается значение nil.
Описание класса tStack с элементами, имеющими вещественные значения, может быть выполнено следующим образом:
Type
tValue = Real; // тип значения элемента стека - вещественный
pItem = ^tItem; // тип указателя на элемент стека
tItem = record // тип элемента стека
Value: tValue; // содержательная часть элемента стека
Next: pItem; // указатель на следующий элемент стека
end; // tItem
tStack = class // класс–стек
Protected
fHead: pItem; // поле - указатель на вершину стека
fSize: Word; // поле - число элементов стека
Public
property Size: Word read fSize; // свойство - число элементов стека
procedure Push(v: tValue); // включение элемента со значением v
function Pop: tValue; // исключение верхнего элемента стека
function Empty: Boolean; // возвращение true, если стек пуст
function TopValue: tValue; // возвращение значения верхнего элемента
procedure Clear; // очистка стека
constructor Create; // конструктор - создание пустого стека
destructor Destroy; override; // деструктор - удаление стека
end; // tStack
Свойство Size доступно только для чтения. Конструктор Create выполняет операции fHead:=nil и fSize:=0. Деструктор Destroy вызывает метод Clear для удаления элементов стека из памяти. Метод Push включает элемент в вершину стека и увеличивает число элементов стека на 1. Метод Pop исключает элемент из вершины стека и уменьшает на 1 размер стека.
4. Реализация основных операций над стеком
Включение элемента со значением v в стек:
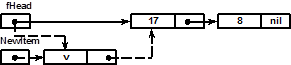
Одинарными линиями показаны связи в исходном состоянии стека, пунктирными – связи, устанавливаемые в процессе выполнения операции. Сначала организуется вспомогательная динамическая переменная с указателем NewItem типа pItem. В поле значения этой переменной записывается значение нового элемента стека, в поле ссылки – адрес верхнего элемента стека, на который указывала ранее переменная fHead. Затем указатель fHead получает значение адреса вновь созданного элемента стека.
Реализация метода включения элемента в стек:
procedure tStack.Push(v:tValue);
Var
NewItem: pItem; // указатель на новый элемент
Begin
NewItem:= New(pItem); // выделение памяти под новый элемент стека
NewItem^.Value:= v; // запись v в поле значения нового элемента
NewItem^.Next:= fHead; // fHead -> в поле ссылки нового элемента
fHead:= NewItem; // перемещение fHead на новый элемент
Inc(fSize); // увеличение числа элементов стека на 1
end; //procedure tStack.Push
Исключение элемента из стека. Сначала читается значение верхнего элемента стека. Затем в переменную DisItem типа pItem из указателя fHead переписывается адрес верхнего элемента стека. Указатель fHead перемещается на элемент стека, следующий за выталкиваемым, и освобождается занимаемая исключаемым элементом память. Схема исключения:
Реализация метода исключения элемента из стека:
function tStack.Pop:tValue;
// Исключение верхнего элемента из стека и возвращение его значения
Var
DisItem: pItem; // указатель на исключаемый элемент
Begin
Pop:= fHead^.Value; // чтение верхнего элемента стека
DisItem:= fHead; // получение адреса исключаемого элемента
fHead:= fHead^.Next; // перемещение вершины на следующий элемент
Dispose(DisItem); // удаление из памяти бывшего верхнего элемента
Dec(fSize); // уменьшение числа элементов стека на 1
end; // function tStack.Pop
Операция Pop неприменима к пустому стеку, поэтому перед ее выполнением необходимо проверять значение признака «стек пуст».
Выработка признака «стек пуст» выполняется следующим образом:
function tStack.Empty: Boolean;
// Возвращает Empty=True, если стек пуст
Begin
Empty:= fHead = nil;
end; // function tStack.Empty
5. Использование стека для преобразования
форм записи выражений.
В инфиксной записи операция разделяет два операнда, в постфиксной – операция следует за двумя операндами, в префиксной – операция предшествует двум операндам. Например:
| Инфиксная запись | Постфиксная запись | Префиксная запись |
| A+B | AB+ | +AB |
| A+B–C | AB+C– | +A–BC |
| A*B+C | AB*C+ | +*ABC |
| A+B*C | ABC*+ | +A*BC |
| (A+B)*C | AB+C* | *+ABC |
v Перевод из инфиксной формы записи выражения в постфиксную (польскую). Инфиксное выражение сканируется слева направо, и в зависимости от вида очередного элемента выражения выполняется одно из следующих действий:
| Элемент выражения | Действие |
| Открывающая скобка | Вталкивание элемента в стек. |
| Операнд | Запись элемента в постфиксную строку. |
| Закрывающая скобка | Выталкивание элементов из стека до первой открывающей скобки и запись их в постфиксную строку, затем выталкивание самой открывающей скобки без записи ее в постфиксную строку. Если перед выполнением этой операции стек оказался пустым, значит, для данной закрывающей скобки не было парной открывающей, т.е. возникла исключительная ситуация. |
| Операция | Если стек не пуст, и приоритет операции ниже (£), чем у верхней операции в стеке, то выталкивание элементов из стека до операции с меньшим приоритетом или до опустошения стека и запись их в постфиксную строку; в противном случае стек не изменяется. Затем вталкивание операции в стек. |
После просмотра выражения выталкиваются из стека и записываются в постфиксную строку все оставшиеся в стеке операции.
v Вычисление значения выражения по его постфиксной записи.
Постфиксное выражение сканируется слева направо и обрабатывается следующим образом:
| Элемент выражения | Действие |
| Операнд | Вталкивание элемента в стек |
| Операция | Выталкивание из стека двух элементов, выполнение операции с ними, запись результата в стек, если стек не пуст. |
v Перевод из инфиксной формы записи выражения в префиксную.
Инфиксное выражение сканируется справа налево, и префиксная строка строится также справа налево. Алгоритм преобразования такой же, как и при преобразовании в постфиксную форму, только открывающие скобки меняются на закрывающие и, наоборот, при определении приоритета операции «£» изменяется на «<», чтобы равноприоритетные операции выполнялись слева направо.
v Вычисление значения выражения по его префиксной записи.
Алгоритм вычисления полностью совпадает с алгоритмом вычисления по постфиксной записи, но префиксная строка сканируется справа налево.
6. Очередь
Очередью называется упорядоченный набор элементов, которые могут исключаться с одного ее конца (называемого началом очереди), а включаться с другого конца (называемого концом очереди). Каждый элемент очереди характеризуется одним и тем же набором полей. Логическая структура очереди:
| Исключение | • | A | B | C | D | E | • | Включение |
| — | — | |||||||
| Начало | Конец |
Очередь функционирует по принципу FIFO (First In – First Out: «первым пришел – первым исключается»). В реальном мире имеется множество примеров очередей: очередь к кассе магазина, очередь задач, обрабатываемых вычислительной машиной. Каждый элемент очереди может содержать одно или несколько полей, число элементов в очереди не ограничено. Очередь, не содержащая ни одного элемента, называется пустой.
7. Операции над очередью
Над очередью q (от англ. queue – очередь) могут быть выполнены следующие операции:
1) включение нового элемента v в конец очереди – Insert (q, v);
2) исключение элемента из начала очереди – Remove (q) и возвращение его значения;
3) выработка признака «очередь пуста» – Empty (q);
4) считывание первого элемента без его удаления – HeadValue (q);
5) считывание последнего элемента очереди – RearValue (q);
6) определение числа элементов очереди Size (q);
8) очистка очереди – Clear (q).
Первые три операции над очередью являются основными. Операции Empty, Size, и Clear для очереди аналогичны соответствующим операциям для стека.
8. Дек
Деком (DEQ – от английского double ended queue, очередь с двумя концами) называется упорядоченный набор элементов, включение и исключение элементов в котором могут осуществляться с любого из двух его концов. Логическая структура дека:
| Включение Исключение | – • | A | B | C | D | E | – • | Исключение Включение |
| — | — | |||||||
| Начало | Конец |
Частные случаи дека – дек с ограниченным входом и дек с ограниченным выходом (включение или исключение элементов осуществляется только с одного из концов дека).
9. Операции над деком
Над деком d могут быть выполнены все операции, определенные для очереди q, а также добавляются две основные операции:
– включение элемента со значением v в начало дека – Push (d, v);
– исключение элемента из конца дека – Delete (d) и возвращение его в качестве значения функции.
10. Реализация очереди и дека
Реализация очереди (дека) с помощью динамических переменных:
При этом вводятся две переменные типа указателя на элемент очереди или дека: Head – на начало, Rear – на конец очереди или дека. В поле ссылки последнего элемента записывается значение nil.
Описание классов tQueue и tDEQ – наследников класса tStack – может быть следующим:
Type
// Описание класса tQueue
tQueue = class (tStack) // класс - очередь
Protected
fRear: pItem; // поле - указатель на конец очереди
Public
procedure Insert(v: tValue); // включение элемента со значением v
function Remove: tValue; // исключение элемента из очереди
function HeadValue:tValue; // возвращение значения первого элемента
function RearValue: tValue; // возвращение значения последнего элемента
constructor Create; // создание пустой очереди
end; // tQueue
// Описание класса tDEQ
tDEQ= class (tQueue) // класс - дек
procedure Push(v: tValue); // включение элемента со знач. v в начало дека
function Delete: tValue; // исключение элемента из конца дека
end; // tDEQ
Класс tQueue наследует у класса tStack поля fHead и fSize, свойство Size, методы Empty, Clear, Destroy и перекрывает метод Create.
Класс tDEQ наследует у класса tQueue поля fHead, fSize, fRear, свойство Size, методы Empty, Clear, Destroy, Insert, Remove, HeadValue, RearValue, Create и перекрывает метод Push класса tStack.
11. Реализация основных операций над очередью и деком
Включение элемента со значением v в очередь выполняется по схеме, приведенной ниже. В схеме не отражена ситуация, когда новый элемент включается в пустую очередь. В этом случае после включения указатели fHead и fRear должны ссылаться на один и тот же вновь созданный элемент, т.е. очередь будет состоять из одного элемента.
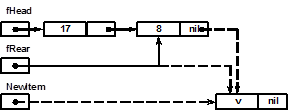
Реализация метода включения элемента в очередь:
procedure tQueue.Insert(v: tValue);
Var
NewItem: pItem; // вспомогательный указатель на новый элемент
Begin
NewItem:= New(pItem); // выделение памяти под новый элемент очереди
NewItem^.Value:= v; // запись v в поле значения нового элемента
NewItem^.Next:= nil; // включенный элемент будет последним
if fRear <> nil // если очередь была не пуста
then fRear^.Next:=NewItem // то новый элемент становится последним
else fHead:= NewItem; // иначе включенный элемент - первый
fRear:= NewItem; // перемещение указателя на конец очереди
Inc(fSize); // увеличение числа элементов очереди на 1
end; // procedure tQueue.Insert
Исключение элемента из начала очереди выполняется по той же схеме, что и исключение элемента из вершины стека. В связи с этим при реализации операции вместо написания последовательности операторов, выполняющих нужные действия, целесообразно использовать наследуемый от типа tStack метод Pop, исключающий элемент из вершины стека. Если элемент исключается из очереди, состоящей из единственного элемента, то после исключения указатель fRear, как и fHead, должен получить значение nil (очередь пуста).
Реализация метода исключения элемента из очереди:
function tQueue.Remove: tValue;
Begin
Remove:= Pop; // исключение элемента из начала методом Pop стека
// Если в очереди был один элемент, то очередь становится пустой:
if fHead = nil then fRear:= nil;
end; // function tQueue.Remove
Включение элемента со значением v в начало дека выполняется так же, как и включение элемента в стек. В связи с этим при реализации операции целесообразно использовать наследуемый от типа tStack метод Push, включающий элемент в вершину стека. Если элемент включается в пустой дек, то после включения указатели fHead и fRear будут ссылаться на один и тот же элемент.
procedure tDEQ.Push(v: tValue);
Begin
inherited Push(v); // включение элемента в начало методом Push стека.
// Если дек был пуст, то элемент становится также и последним:
if fRear = nil then fRear:= fHead;
end; // procedure tDEQ.DPush
Исключение элемента из конца дека выполняется по следующей схеме. Читается значение последнего элемента дека, и в переменную DisItem типа pItem из указателя fRear переписывается адрес этого элемента. Затем с помощью передвигаемого по элементам дека указателя Item типа pItem отыскивается предпоследний элемент дека, адрес которого записывается в переменную fRear, а в поле ссылки этого элемента – значение nil (элемент становится последним в деке). Элемент с указателем DisItem исключается из памяти. Если исключаемый элемент является единственным в деке (признак этого – равенство значений fHead и fRear), то после чтения значения исключаемого элемента необходимо присвоить переменным fHead и fRear значение nil.
function tDEQ.Delete: tValue;
Var
DisItem, PredItem: pItem; // исключаемый и предпоследний элементы
Begin
Delete:= fRear^.Value; // возвращение последнего элемента дека
DisItem:= fRear; // исключаемый элемент - последний
if fHead <> fRear // если в деке более одного элемента
then begin // то выполняется поиск предпоследнего элемента,
PredItem:= fHead;
while PredItem ^.Next<>fRear do PredItem:= PredItem ^.Next;
fRear:= PredItem; fRear^.Next:= nil; // который становится последним.
End
else begin // если в деке один элемент,
fHead:= nil; fRear:= nil; // то после исключения дек становится пустым
end;
Dispose(DisItem);
Dec(fSize); // уменьшение числа элементов дека на 1
end; // function tDEQ.Delete
Операции исключения элемента из очереди и дека неприменимы к пустым структурам, поэтому перед их выполнением необходимо анализировать значение признака «очередь пуста» или «дек пуст».
12. Итератор
Итератор – обобщение итерационных методов, имеющихся в большинстве языков программирования. Итераторы позволяют выполнить итерации для произвольных типов данных. Примеры функций итераторов: выдача элементов некоторого множества в произвольном порядке; выдача элементов набора в заданном порядке, например, от меньшего к большему; выдача элементов очереди от начала к концу и т.д.
С помощью итераторов реализуются более сложные операции с абстрактными типами данных, например, вычисление суммы элементов очереди, печать всех элементов очереди, т.е. такие операции, которые нецелесообразно включать в набор операций класса.
Итератор за одно обращение к нему выдает только один результат (например, значение одного элемента очереди). После выдачи элемента работа итератора не заканчивается. Он готов продолжить выдачу элементов, причем все текущие значения локальных переменных сохраняются при следующем обращении к итератору, т.е. вход в итератор осуществляется, как бы минуя его заголовок и начальные установки итератора.
Пример. Суммирование элементов очереди без итератора.
Решение этой задачи требует создания вспомогательной очереди, при удалении элементов из которой можно суммировать значения элементов.
Var
sum: tValue;
q, q1: pQueue; // основная и вспомогательная очереди
Begin
...
sum:=0;
q1:=q^.Copy; // копирование основной очереди во вспомогательную
while not q1^.Empty do
sum:=sum+q1^.Remove;
q1^.Destroy;
...
end.
Использование итератора позволит избежать потерь по времени и пространству при копировании очереди (или при выполнении других операций, требующих последовательного обращения к элементам структуры).
Итератор включает в себя три операции: 1) инициализация итератора; 2) выдача очередного элемента; 3) проверка, все ли элементы выданы.
Итератор удобно реализовать в виде операций в абстрактном типе данных (например, в очереди). Для этого в секцию protected описания типа tQueue добавим новое поле
fItem:pItem; // указатель на элемент очереди
и методы:
procedure IterInit:
function IterDone: Boolean;
function IterNext:tValue;
Реализация методов итератора:
procedure tQueue.IterInit; // инициализация итератора
Begin
fItem:=fHead;
end; // tQueue.IterInit
function tQueue.IterDone: Boolean; // True, если все элементы выданы
Begin
IterDone:= fItem = nil;
end; // tQueue.IterDone
function tQueue.IterNext: tValue; // выдача итератором очередного элемента
Begin
if not IterDone
Then begin
IterNext:=fItem^.Value;
fItem:=fItem^.Next;
end;
end; // tQueue.IterNext
Пример. Суммирование элементов очереди с итератором.
Var
sum: tValue;
q: pQueue;
Begin
...
sum:=0; q^.IterInit;
while not q^.IterDone do sum:=sum+q^.IterNext;
...
end.
Лабораторная работа 1.
Стеки, очереди, деки
Задание
Опишите и реализуйте класс, необходимый для решения задачи, указанной в вашем варианте задания, и реализуйте его методы.
Составьте программу решения задачи с использованием динамической структуры данных, реализованной в виде класса.
В этой и во всех последующих лабораторных работах должны быть выполнены требования, приведённые ниже в рамке.
Описание класса и реализацию его методов разместите в модуле. Для выполнения операций, не включенных в набор операций класса, например вывод элементов структуры, реализуйте и используйте итератор, либо напишите соответствующий метод.
Исходные данные необходимо считывать из файла и вместе с результатами работы помещать в файл результатов.
В программе следует предусмотреть вывод необходимых промежуточных и всех окончательных результатов решения задачи. По окончании работы экземпляры структур очистить и освободить память, занимаемую ими.
Предусмотреть генерацию и обработку исключительных ситуаций, которые могут возникнуть при выполнении операций со структурами данных.
Варианты заданий
1. Проверить правильность расстановки скобок в арифметическом выражении (допустимы четыре типа скобок: круглые, квадратные, фигурные и угловые). Для слежения за скобками воспользоваться стеком.
2. Создать стек, каждый элемент которого является совокупностью двух целых значений. Заменить нулевыми все элементы с заданной суммой значений.
3. Сформировать стек с элементами – строками. Прочитать три нижних элемента стека и поменять местами верхний и нижний элементы.
4. Сформировать две очереди с фамилиями клиентов. Слить обе очереди в третью, расположив клиентов через одного.
5. Прочитать из входного файла последовательность слов Pop и Push. Слово Push вталкивается в стек и выводится число элементов стека, при чтении слова Pop выполня