Здесь и в дальнейшем при одновременном использовании нескольких различных систем счисления основание системы к которой относится число будем указывать в виде нижнего индекса.
10101101.1012 = 1 
27+ 0 26+ 1 25+ 0 24+ 1 23+ 1 22+ 0 21+ 1 20+ 1 2-1+ 0 2-2+ 1 2-3 = 173.62510
б) Перевести 703.048 
"10" с.с.
703.048 = 7 82+ 0 81+ 3 80+ 0 8-1+ 4 8-2 = 451.062510
в) Перевести B2E.416 "10" с.с.
B2E.416 = 11 162+ 2 161+ 14 160+ 4 16-1 = 2862.2510
Перевод целых десятичных чисел в недесятичную систему счисления осуществляется последовательным делением десятичного числа на основание той системы, в которую оно переводится, до тех пор, пока не получится частное меньшее этого основания. Число в новой системе записывается в виде остатков деления, начиная с последнего.
Пример.
а) Перевести 18110 "8" с.с.
Результат: 18110 = 2658
| б) Перевести 62210 "16" с.с.
Результат: 62210 = 26E16
|
Перевод правильных дробей из десятичной системы счисления в недесятичную.
Для перевода правильной десятичной дроби в другую систему эту дробь надо последовательно умножать на основание той системы, в которую она переводится. При этом умножаются только дробные части. Дробь в новой системе записывается в виде целых частей произведений, начиная с первого.
Пример.
Перевести 0.312510 "8" с.с.
Результат: 0.312510 = 0.248
Замечание. Конечной десятичной дроби в другой системе счисления может соответствовать бесконечная (иногда периодическая) дробь. В этом случае количество знаков в представлении дроби в новой системе берется в зависимости от требуемой точности.
Пример.
Перевести 0.6510 "2" с.с. Точность 6 знаков.
Результат: 0.6510 
0.10(1001)2
Для перевода неправильной десятичной дроби в систему счисления с недесятичным основанием необходимо отдельно перевести целую часть и отдельно дробную.
Пример.
Перевести 23.12510 "2" с.с.
| 1) Переведем целую часть: | 2) Переведем дробную часть: |
| 
|
Таким образом: 2310 = 101112; 0.12510 = 0.0012.
Результат: 23.12510 = 10111.0012.
Необходимо отметить, что целые числа остаются целыми, а правильные дроби - дробями в любой системе счисления.
Для перевода восьмеричного или шестнадцатеричного числа в двоичную форму достаточно заменить каждую цифру этого числа соответствующим трехразрядным двоичным числом (триадой) (Таб. 1) или четырехразрядным двоичным числом (тетрадой) (Таб. 1), при этом отбрасывают ненужные нули в старших и младших разрядах.
Пример.
а) Перевести 305.48 "2" с.с.
| б) Перевести 7B2.E16 "2" с.с.
|
Для перехода от двоичной к восьмеричной (шестнадцатеричной) системе поступают следующим образом: двигаясь от точки влево и вправо, разбивают двоичное число на группы по три (четыре) разряда, дополняя при необходимости нулями крайние левую и правую группы. Затем триаду (тетраду) заменяют соответствующей восьмеричной (шестнадцатеричной) цифрой.
Пример.
а) Перевести 1101111001.11012 "8" с.с.
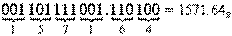
| б) Перевести 11111111011.1001112 "16" с.с.
|
Перевод из восьмеричной в шестнадцатеричную систему и обратно осуществляется через двоичную систему с помощью триад и тетрад.
Пример. Перевести 175.248 "16" с.с.
Результат: 175.248 = 7D.516.
3 Двоичная арифметика.
Правила выполнения арифметических действий над двоичными числами задаются таблицами двоичных сложения, вычитания и умножения.
| Таблица двоичного сложения | Таблица двоичного вычитания | Таблица двоичного умножения |
| 0+0=0 0+1=1 1+0=1 1+1=10 | 0-0=0 1-0=1 1-1=0 10-1=1 | 0  0=0 0 1=0 1 0=0 1 1=1
|
При сложении двоичных чисел в каждом разряде производится сложение цифр слагаемых и переноса из соседнего младшего разряда, если он имеется. При этом необходимо учитывать, что 1+1 дают нуль в данном разряде и единицу переноса в следующий.
Пример. Выполнить сложение двоичных чисел:
а) X=1101, Y=101;
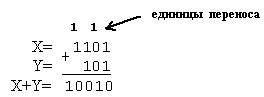Результат 1101+101=10010.
| б) X=1101, Y=101, Z=111;
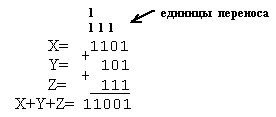Результат 1101+101+111=11001.
|
При вычитании двоичных чисел в данном разряде при необходимости занимается 1 из старшего разряда. Эта занимаемая 1 равна двум 1 данного разряда.
Пример. Заданы двоичные числа X=10010 и Y=101. Вычислить X-Y.
Результат 10010 - 101=1101.
Умножение двоичных чисел производится по тем же правилам, что и для десятичных с помощью таблиц двоичного умножения и сложения.
Пример. 1001 101=?
Результат 1001 101=101101.
Деление двоичных чисел производится по тем же правилам, что и для десятичных. При этом используются таблицы двоичного умножения и вычитания.
Пример. 1100.011: 10.01=?
Результат 1100.011: 10.01=101.1.
Упражнения
1. Перевести следующие числа в десятичную систему счисления:
а) 1101112; б) 563.448; в) 1C4.A16.
2. Перевести число 463.04 из "10" с.с в "2", "8", "16" с.с.
3. Перевести следующие числа в двоичную систему счисления:
а) 172.328; б) 7BF.52A16.
4. Перевести следующие числа из одной системы счисления в другую:
а) 312.78 "16" с.с.; б) 5B.F16 "8" с.с.
5. Заданы двоичные числа X и Y. Вычислить X+Y и X-Y, если:
X=1101001; Y=101111
6. Заданы двоичные числа X и Y. Вычислить X*Y и X/Y, если:
X=100101.011; Y=110.1
ОСНОВНЫЕ ПОНЯТИЯ АЛГЕБРЫВЫСКАЗЫВАНИЙ
Основное понятие булевой алгебры – это высказывание.
Высказывание – является умозаключением, которое может принимать значение либо истинно, либо ложно (третьего не дано). Высказывания обычно обозначают большими буквами латинского алфавита. Значение истинно принято обозначать одним из следующих символов: «1», «И», «TRUE». Ложно: «0», «Л», «FALSE».
Например, А = «Идёт снег»
Из простых высказываний при помощи логических операций можно получить высказывание сложное.
Логические операции
1. Конъюнкция (&, ^, AND, И) двух высказываний A и B это новое высказывание C, которое истинно тогда и только тогда, когда истинны оба входящих высказывания. Конъюнкция – это логическое умножение.
Таблица истинности для данной операции имеет вид:
2. Дизъюнкция (Ú, OR, ИЛИ) – это логическая сума, в результате которой образуется новое высказывание, имеющее значение истина, если истинно хотя бы одно из входящих высказываний.
Таблица истинности дизъюнкции:
3. Импликация ( 
, следование) двух высказываний A и B (А именуется посылкой, а B заключением) - это новое высказывание C, которое ложно только тогда, когда посылка истинна, а заключение ложно.
Таблица истинности такой операции следующая:
4. Эквиваленцией ( 
, º, равносильность) двух высказываний A и B является новое высказывание C, которое истинно только тогда, когда оба входящих высказывания имеют одинаковое значение истинности.
Таблица истинности:
5. Отрицание ( é, 
, NOT, не) это унарная операция, в результате которой получаем высказывание, которое истинно, когда исходное высказывание ложно, и ложно, когда исходное высказывание истинно.
Таблица истинности:
5. Исключающее или
Таблица истинности:
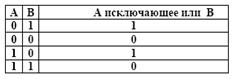
Приоритеты выполнения операций: сначала выполняются операции в скобках, затем отрицание, конъюнкция и дизъюнкция слева направо, импликация, эквиваленция.
Пример: Построить таблицу истинности логической функции 
.
Для построения таблицы истинности, необходимо для двух входящих высказываний С и В перебрать все возможные варианты отношений (оба ложны, оба истинны, одно истинно – другое ложно), а затем последовательно, по столбцам, в соответствии с приоритетами выполнить все логические операции:
Упражнения
1. Построить таблицу истинности высказывания 
.
2. Определить, верно ли тождество 
.