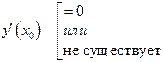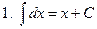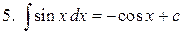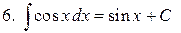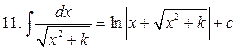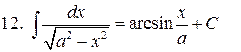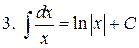ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
Производные некоторых элементарных функций
| 1. | 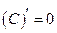
| 
| 
|
| 2. | 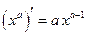 
| 

| |
| 3. |  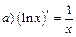
| 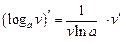 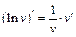
|
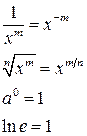
|
| 4. |   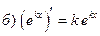
|  
| |
| 5. | 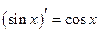 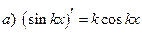
| 
| |
| 6. | 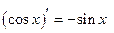 
| 
| |
| 7. | 
| 
| |
| 8. | 
| 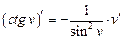
| |
| 9. | 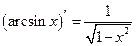
| 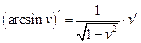
| |
| 10. | 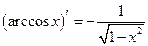
| 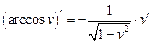
| |
| 11. | 
| 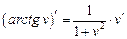
| |
| 12. | 
| 
|
Техника дифференцирования
Занятие 1
Устно: 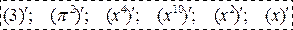
|
1. Вычислить первую производную функции

Устно: 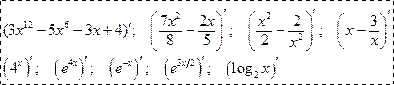
|
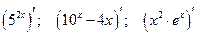
Устно: 
|
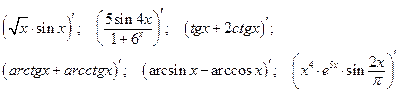
Производные сложных функций
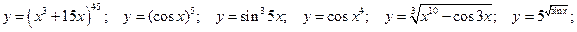
Занятие 2.
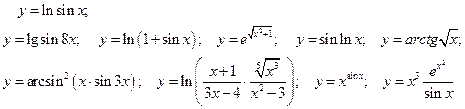
Устно: 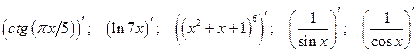
|
2. Найти значение  :
: 
3. Найти 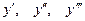 при
при 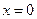 :
:  .
.
4. Функция  задана уравнением
задана уравнением  . Найти
. Найти 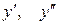 при
при 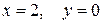 .
.
Устно: Найти дифференциал функции
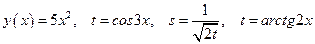
|
Дома.
1. Найти  :
: 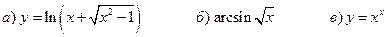 .
.
2. Найти значения 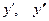 при
при 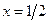 :
:  .
.
3. Дано: 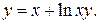 Найти
Найти  .
.
Ответы: 1. 
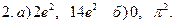 3.
3. 
ПРИЛОЖЕНИЯ ПРОИЗВОДНОЙ
Занятие 1.
Правило Лопиталя
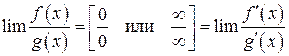
|
Вычислить пределы функций
| 5.100 | 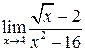
| 5.103 | 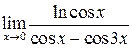
| 5.106 | 
|
| 5.101 | 
| 5.104 | 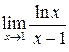
| 5.107 | 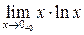
|
| 5.102 | 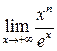
| 5.105 | 
| 5.108 | 
|
Дома.
Вычислить пределы, используя правило Лопиталя
| 5.109 | 
| 5.111 | 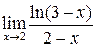
| 5.113 | 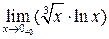
|
| 5.110 | 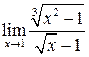
| 5.112 | 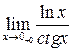
| 5.114 | 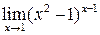
|
Ответы.
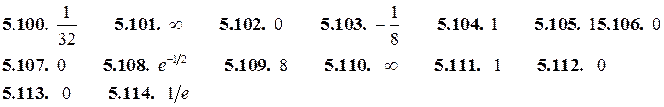
Занятие 2.
Исследование функции
1. ОДЗ
 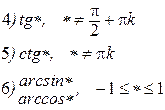 2. а) Вертикальная асимптота
2. а) Вертикальная асимптота 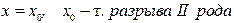 б) Наклонная асимптота
б) Наклонная асимптота 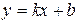 , где , где 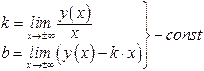
5. |
Провести полное исследование и построить график функции
| 5.115 | 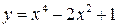
| 5.116 | 
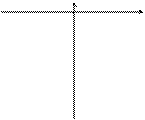
| 5.117 | 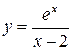
|

Устно. Для функции  указать точки экстремума, точки перегиба, интервалы возрастания, выпуклости. указать точки экстремума, точки перегиба, интервалы возрастания, выпуклости.
|  
|
5.118. По графику функции  построить эскизы графиков
построить эскизы графиков 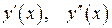
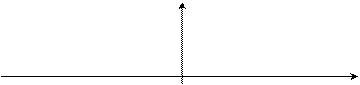

5.119. Найти наибольшее и наименьшее значения функции на отрезке
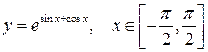 .
.
5.120. Какими должны быть размеры банки цилиндрической формы, чтобы при фиксированном объеме площадь ее поверхности была наименьшей?
Дома.
Построить графики функций
| 5.121 | 
| 5.122 | 
|
5.123. Найти наибольшее и наименьшее значения функции на отрезке
 .
.
5.124. Из пункта А в пункт В отправляется лодка со скоростью 10 км\ч. Из пункта В в С отправляется в это же время катер со скоростью 15 км\ч. Через какое время расстояние между ними будет наименьшим, если от А до В 190 км и угол АВС –  ?
?
Ответы.
5.115
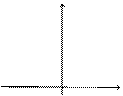 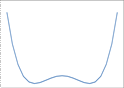
| 5.116
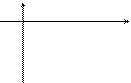 
|
5.117
 
|
  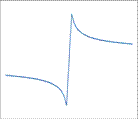
| 
 
|
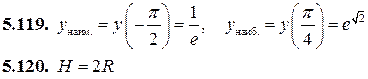
5.121.
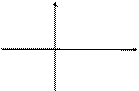 
| 5.122.
 
|
5.124. Через 7 часов.
ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ

Поверхность уровня
 Полный дифференциал
Полный дифференциал
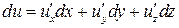 Производная неявно заданной функции
Производная неявно заданной функции 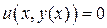
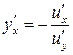 Градиент
Градиент
 Производная по направлению
Производная по направлению
 Локальный экстремум
Локальный экстремум
 Касательная плоскость и нормаль к поверхности
Касательная плоскость и нормаль к поверхности 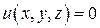 в точке в точке 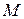
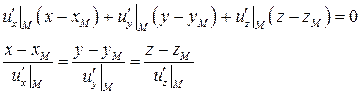
|
Занятие 1.
Область определения. Поверхность уровня.
Частные производные. Дифференциал
6.1. Изобразить на плоскости область определения функции
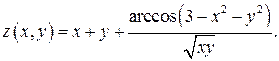
6.2. Для функции 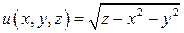 построить поверхность уровня
построить поверхность уровня 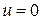 , поверхность уровня, проходящую через точку
, поверхность уровня, проходящую через точку  .
.
 Устно. Восстановить функцию двух переменных по линиям уровня Устно. Восстановить функцию двух переменных по линиям уровня
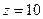
|
6.3. Найти частные производные первого порядка

Устно. Найти 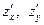 : :
 г) г) 
|
6.4. Найти:  , если
, если  .
.
Устно. Найти 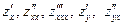 : :
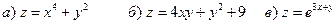
|
6.5. Доказать тождества
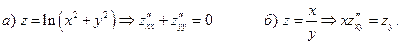
Дома.
6.6. Изобразить на плоскости область определения функции 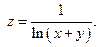
6.7. Вычислить  , если
, если 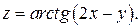
6.8. Найти 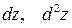 , если
, если 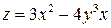 .
.
6.9. Доказать тождество 
Ответы.
 | |||
 | |||
6.1. 6.2.

 6.6.
6.6.
6.6.

Занятие 2.
Производная сложной функции. Производная неявно заданной функции.
Производная по направлению. Градиент
6.10. Найти  :
: 
6.11. Найти 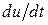 :
: 
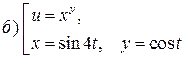
6.12. Найти 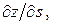
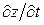 :
: 
6.13. Дано: 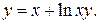 Найти
Найти  .
.
6.14. Дано: 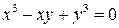 . Найти
. Найти 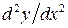 при условии
при условии 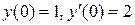 .
.
6.15. Найти производную функции 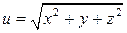 в точке
в точке  по направлению к
по направлению к 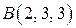 .
.
6.16. Найти производную функции 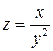 в точке
в точке  в направлении, составляющем угол
в направлении, составляющем угол  с положительным направлением оси
с положительным направлением оси 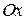 .
.
6.17. Найти градиент и наибольшую скорость возрастания функции 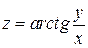 в точке
в точке 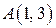 .
.
6.18. В какой точке градиент функции  коллинеарен вектору
коллинеарен вектору 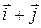 ?
?
Дома.
6.19. а) 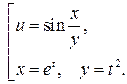
 –?
–? 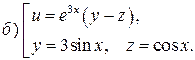
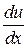 –?
–?
6.20. Функция  задана уравнением
задана уравнением  . Найти
. Найти 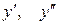 при
при 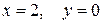 .
.
6.21. Найти производную функции  в точке
в точке 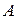 по направлению вектора
по направлению вектора  , где
, где 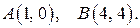
6.22. Найти градиент и наибольшую скорость возрастания функции 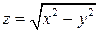 в точке
в точке 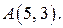
Ответы.

Занятие 3.
Касательная плоскость и нормаль к поверхности.
Локальный и глобальный экстремумы
Локальный экстремум.
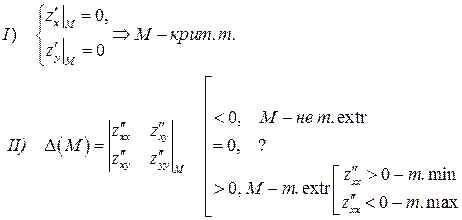 Касательная плоскость и нормаль к поверхности
Касательная плоскость и нормаль к поверхности 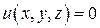 в точке в точке 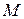 . .
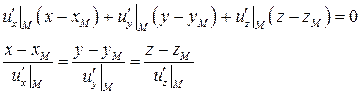
|
6.23. Найти уравнения касательной плоскости и нормали к поверхности 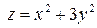 в точке
в точке  .
.
6.24. Составить уравнение плоскости, касательной к поверхности 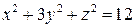 , параллельную плоскости
, параллельную плоскости 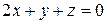 .
.
6.25. Исследовать на экстремум функцию  .
.
6.26. Найти наибольшее и наименьшее значения функции  в замкнутом треугольнике, ограниченном осями координат и прямой
в замкнутом треугольнике, ограниченном осями координат и прямой 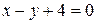 .
.
Дома.
6.27. Найти уравнения касательной плоскости и нормали к поверхности 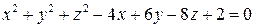 в точке
в точке  .
.
6.28. Исследовать на экстремум функцию 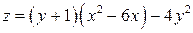 .
.
6.29. Найти наибольшее и наименьшее значения функции 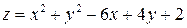 в замкнутом прямоугольнике:
в замкнутом прямоугольнике:  .
.
Ответы.
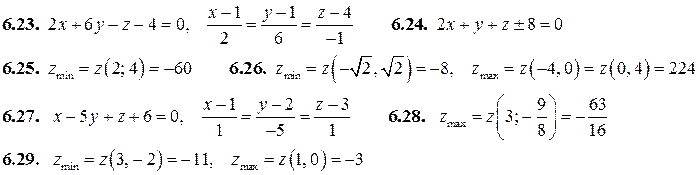
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
|
Занятие 1.
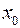 - критическая точка, если
- критическая точка, если