Устно. 
|
| 7.1. | 
| 7.4. | 
|
| 7.2. | 
| 7.5. | 
|
| 7.3. | 
| 7.6. | 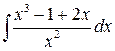
|
Устно.  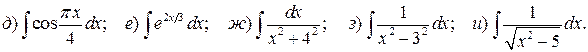
|
| 7.7. | 
| 7.11. | 
|
| 7.8. | 
| 7.12. | 
|
| 7.9. | 
| 7.13. | 
|
| 7.10. | 
| 7.14. | 
|
Ответы.
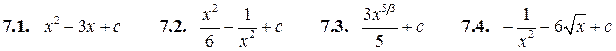


Занятие 2.
Метод подстановки
| 7.15. | 
| 7.19. | 
|
| 7.16. | 
| 7.20. | 
|
| 7.17. | 
| 7.21. | 
|
| 7.18. | 
| 7.22. | 
|
Устно. 
|
| 7.23. | 
| 7.30. | 
|
| 7.24. | 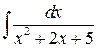
| 7.31. | 
|
| 7.25. | 
| 7.32. | 
|
| 7.26. | 
| 7.33. | 
|
| 7.27. | 
| 7.34. | 
|
| 7.28. | 
| 7.35. | 
|
| 7.29. | 
| 7.36. | 
|
Устно. 
|
Дома.
| 7.37. | 
| 7.44. | 
|
| 7.38. | 
| 7.45. | 
|
| 7.39. | 
| 7.46. | 
|
| 7.40. | 
| 7.47. | 
|
| 7.41. | 
| 7.48. | 
|
| 7.42. | 
| 7.49. | 
|
| 7.43. | 
| 7.50. | 
|
Ответы.



Занятие 3.
Интегрирование по частям
| 7.51. | 
| 7.56. | 
|
| 7.52. | 
| 7.57. | 
|
| 7.53. | 
| 7.58. | 
|
| 7.54. | 
| 7.59. | 
|
| 7.55. | 
| 7.60. | 
|
Дома.
| 7.61. | 
| 7.64. | 
|
| 7.62. | 
| 7.65. | 
|
| 7.63. | 
| 7.66. | 
|
Ответы.




Занятие 4.
Интегрирование рациональных дробей


|
Устно:  \ \
|
| 7.67. | 
| 7.71. | 
|
| 7.68. | 
| 7.72. | 
|
| 7.69. | 
| 7.73. | 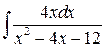
|
| 7.70. | 
| 7.74. | 
|
Представить правильные дроби в виде суммы простейших дробей
| 7.75. | 
| 7.77. | 
|
| 7.76. | 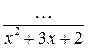
| 7.78. | 
|
| 7.79. | 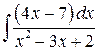
| 7.81. | 
|
| 7.80. | 
| 7.82. | 
|
Дома.
| 7.83. | 
| 7.85. | 
|
| 7.84. | 
| 7.86. | 
|
Ответы



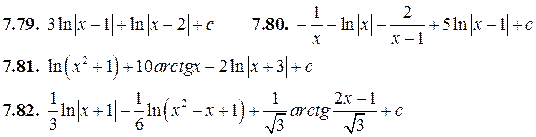

Занятие 5.
Интегрирование тригонометрических функций
| 7.87. | 
| 7.91. | 
|
| 7.88. | 
| 7.92. | 
|
| 7.89. | 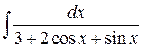
| 7.93. | 
|
| 7.90. | 
| 7.94. | 
|
Дома.
| 7.95. | 
| 7.98. | 
|
| 7.96. | 
| 7.99. | 
|
| 7.97. | 
| 7.100. | 
|
Ответы.


Занятие 6.
Интегрирование некоторых иррациональных функций
| 7.101. | 
| 7.104. | 
|
| 7.102. | 
| 7.105. | 
|
| 7.103. | 
| 7.106. | 
|
Дома
| 7.107. | 
| 7.109. | 
|
| 7.108. | 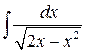
| 7.110. | 
|
Ответы.
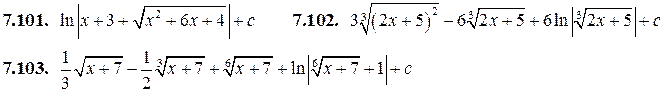

Занятие 7.
ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ
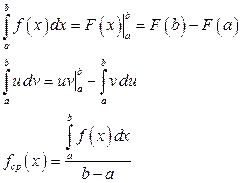
|
1. Вычислить определенный интеграл ( )
)
| 8.1. | 
| 8.4. | 
|
| 8.2. | 
| 8.5. | 
|
| 8.3. | 
| 8.6. | 
|
Устно.  
|
 Устно. Найти среднее значение функции на отрезке Устно. Найти среднее значение функции на отрезке 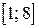 .
1 8 .
1 8
|
8.7. Найти среднее значение функции 
Исследовать на сходимость несобственные интегралы
| 8.8. | 
| 8.10. | 
|
| 8.9. | 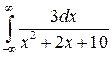
| 8.11. | 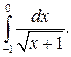
|
Дома.
| 8.12. | 
| 8.13. | 
|
Исследовать на сходимость несобственные интегралы
| 8.14. | 
| 8.16. | 
|
| 8.15. | 
| 8.17. | 
|
Ответы.

Занятие 8.
Приложения определенного интеграла
Найти площадь фигуры, ограниченной линиями
8.18. См. рисунок
 |
| 8.19. | 
| 8.22. |  (под одной аркой)
(под одной аркой)
|
| 8.20. | 
| 8.23. | 
|
| 8.21. | 
| 8.24. | 
|
8.25. Найти объем тела, образованного вращением кривой 
а) вокруг оси 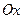 ; б)вокруг оси
; б)вокруг оси  .
.
Дома.
Найти площадь фигуры, ограниченной линиями
| 8.26. | 
| 8.28. | 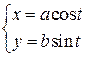
|
| 8.27. | 
| 8.29. | 
|
8.30. Вывести формулу объема конуса, если радиус основания -  , высота -
, высота -  .
.
Ответы.

Занятие 9.

|
Найти длину дуги
| 8.31. | 
| 8.32. | 
| 8.33. | 
|
Найти момент инерции относительно оси  однородного (
однородного ( ) стержня, заданного уравнением
) стержня, заданного уравнением
| 8.34. | 
| 8.35. | 
|
 8.36. Найти работу по выкачиванию жидкости плотности
8.36. Найти работу по выкачиванию жидкости плотности  из корыта, имеющего форму полукруглого цилиндра указанных на рисунке размеров.
из корыта, имеющего форму полукруглого цилиндра указанных на рисунке размеров.
Дома.
Найти длину дуги
| 8.37. | 
| 8.38. | 
| 8.39. | 
|
8.40. Найти моменты инерции относительно координатных осей однородного ( ) стержня, заданного уравнением
) стержня, заданного уравнением  .
.
8.41. Найти работу по выкачиванию жидкости плотности  из пирамиды с квадратным основанием
из пирамиды с квадратным основанием  высоты
высоты  .
.
Ответы.

КРАТНЫЕ ИНТЕГРАЛЫ
Занятие 10.
Двойной интеграл в ДСК
 
|  
|
Представить интеграл 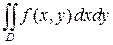 по указанной области в виде повторного.
по указанной области в виде повторного.
| 9.1. | 
| 9.3. | 
| ||
| 9.2. | 
| 9.4. | Четырехугольник

| ||
| 9.5.См. рисунок. |
| ||||
Изобразить область интегрирования
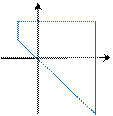
| 96. | 
| 9.7. | 
|
Устно. Расставить пределы интегрирования
 

|
Изменить порядок интегрирования
| 9.8. | 
| 9.9. | 
|
Вычислить интегралы
| 9.10. | 
| 9.11. | 
| 9.12. | 
|
Устно. Найти среднее значение функции  в области в области 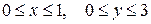 . .

|
9.13. Найти среднее значение функции  в области, ограниченной линиями
в области, ограниченной линиями 
Дома.
Представить 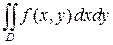 по области
по области  в виде повторного двумя способами
в виде повторного двумя способами
| 9.14. | 
| 9.15. | 
| 9.16. | 
|
9.17. Изменить порядок интегрирования  .
.
Ответы.


9.6., 9.7

Занятие 11.
Двойной интеграл в ПСК. Приложения двойного интеграла
|
Представить интеграл 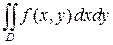 по области, ограниченной данными линиями, в виде повторного, перейдя в полярную систему координат.
по области, ограниченной данными линиями, в виде повторного, перейдя в полярную систему координат.
| 9.18. | 
| 9.19. | 
|
9.19. Найти площадь пластины

9.20. Найти массу пластины  , если поверхностная плотность
, если поверхностная плотность  .
.
9.21. Найти центр масс однородного полукруга  .
.
9.22. Найти объем тела 
Дома:
Представить интеграл 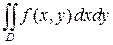 по области
по области 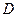 : в виде повторного в ПСК.
: в виде повторного в ПСК.
| 9.24. | 
| 9.25. | 
|
9.26. Найти площадь области 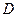 :
:  .
.
9.27. Найти массу пластины 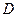 :
:  с поверхностной плотностью
с поверхностной плотностью  .
.
9.28. Найти координаты центра масс пластины  , если поверхностная плотность
, если поверхностная плотность  .
.
Ответы.

. Занятие 13.
Тройной интеграл
|

 Расставить пределы интегрирования
Расставить пределы интегрирования  .
.
См. рисунок.
9.30. Вычислить интеграл 
9.31. Найти объем тела, ограниченного поверхностями: 
9.32. Найти координаты центра масс однородного 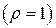 тела, ограниченного поверхностями:
тела, ограниченного поверхностями: 
9.33. Найти момент инерции однородного  цилиндра
цилиндра  относительно оси
относительно оси 
9.34. Вычислить интеграл 
Дома.
9.35. Найти среднее значение функции  в области:
в области: 
9.36. Вычислить интеграл 
9.37. Найти объем тела: 
Ответы.

ЧИСЛОВЫЕ РЯДЫ
Занятие 1.
Знакоположительные ряды

Теорема сравнения 1. Теорема сравнения 2. Теорема сравнения 3. Признак Даламбера. Радикальный признак Коши. Интегральный признак Коши. ряд |
Знакочередующиеся ряды

Теорема Лейбница. Если 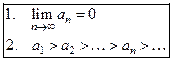 , то ряд
, то ряд  сходится.
сходится.
Если ряд  сходится и ряд
сходится и ряд  сходится, то ряд
сходится, то ряд  сходится а бсолютно.
сходится а бсолютно.
Если ряд  сходится, а ряд
сходится, а ряд  расходится, то ряд
расходится, то ряд  сходится условно.
сходится условно.
Если ряд  сходится, то
сходится, то  .
.





 ССК
ССК





 и
и  сходятся или расходятся одновременно.
сходятся или расходятся одновременно. .
. .
.
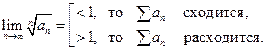

 и интеграл
и интеграл  сходятся или расходятся одновременно.
сходятся или расходятся одновременно. :
1. найти первые три члена ряда
:
1. найти первые три члена ряда  по заданному общему члену
по заданному общему члену  ;
2. найти формулу для общего члена ряда
;
2. найти формулу для общего члена ряда
 б)
б)  .
3. проверить необходимое условие сходимости ряда:
.
3. проверить необходимое условие сходимости ряда: 


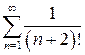









 .
.







