Задача 1. Объем выборки.
Для нормального существования микроорганизмов в почве национального парка Приволжский, необходимо чтобы средний объем кислорода, содержащегося в почве, имел некоторое заданное значение. В качестве оценки этого объема принято использовать выборочное среднее по различным измерениям почвы из разных уголков парка. Из предыдущих исследований известно, что стандартное отклонение объема кислорода составляет 7г. Найти минимальное количество измерений, которое необходимо провести, чтобы при погрешности более 3г риск не превышал 1%.
Решение: Формула n=z2*s2/b2.
z находится из таблицы нормального распределения и равно 2.58.
b =3
s=7.
Ответ: 15, а не 14.046, т.к. необходимо округлять в большую сторону.
Задача 1. На ДОМ. свойства оценок
В течение двух дней исследовательская группа проводила опрос населения некоторого города с целью выяснить уровень поддержки действующей администрации среди местного населения, для чего респондентам предлагалось оценить своё отношение к действиям администрации по 10-балльной шкале. В течение первого дня было опрошено 200 респондентов, среди которых средний балл составил 
. В течение второго дня было опрошено 300 респондентов и средний балл составил 
.
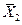К сожалению, все результаты опроса, кроме значений и 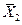, были утеряны, и исследователи не могли вспомнить, сколько респондентов было опрошено за эти два дня. В результате, для среднего по генеральной совокупности (математического ожидания) было решено использовать оценку 
.
Покажите, что оценка 
является несмещённой для среднего по генеральной совокупности. Рассчитайте, насколько её дисперсия больше дисперсии выборочного среднего 
, рассчитанного по всем 500 наблюдениям. Считайте, что все наблюдаемые случайные величины независимы и имеют одинаковые математическое ожидание и дисперсию.
|
|
Решение:
Пусть 
- среднее по генеральной совокупности, а 
- дисперсия. Тогда 
. Следовательно, 
. Оценка есть несмещённая оценка для среднего по генеральной совокупности.
Найдём дисперсии средних за оба дня: 
, 
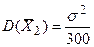. Отсюда 
.
Дисперсия среднего, рассчитанного по всем 500 наблюдениям, равна 
. Значит, дисперсия оценки больше в 
раза.
Задача 2. Свойства оценок. Случайные величины 
независимы, ряд распределения каждой из величин 
известен с точностью до параметра :
| Возможные значения величины :
| 
|
| 
|
| Вероятности этих значений: | 0.3 | 0.5 | 0.2 |
Пусть 
- среднее значение величин : 
.
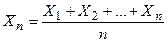а) Найдите математическое ожидание и дисперсию .
б) Достаточно ли полученных в пункте (а) результатов, чтобы утверждать, что является состоятельной оценкой для параметра ?
Решение:
а) Воспользуемся свойствами математического ожидания и дисперсии:
;
- последнее равенство верно в силу независимости .
Найдём ожидание и дисперсию величины : 
.
Отсюда:
; 
Обратим внимание, что в числителе выражения для дисперсии – сумма арифметической прогрессии: 
. Так что 
б) Достаточное условие состоятельности оценки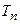 
для параметра 
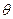состоит из двух равенств:
1) 
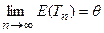, 2) 
.
Оценка удовлетворяет первому равенству: 
.
Второе, однако, не выполняется: 
Поэтому из знания математического ожидания и дисперсии нельзя заключить, что оценка состоятельна.
Задача 3. Свойства оценок. На ДОМ. Имеются две независимые несмещённые оценки параметра θ, обозначим их 
и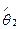 
, а их дисперсии соответственно 
и 
. Найдите значение 
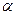, при котором оценка 
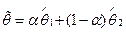будет иметь наименьшую дисперсию. Будет ли 
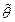несмещённой оценкой для θ?
|
|
Решение:
Найдём дисперсию оценки :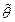 
.
Для нахождения минимума по 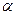приравняем к нулю первую производную полученного выражения:
.
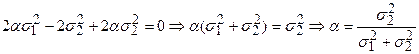Вторая производная оказывается положительной: 
(если, конечно, хотя бы одна из дисперсий не равна нулю). Таким образом, найдённое значение 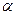действительно доставляет минимум дисперсии .
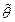Несмещённость оценки проверяется легко:
Задача 4. Свойства оценок. Имеются n наблюдений (n ≥3), представляемых независимыми одинаково распределёнными случайными величинами с математическим ожиданием и дисперсией 
. Определите, какие из приведённых ниже оценок 
, 
и 
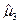являются несмещёнными? Какая из несмещённых оценок является относительно более эффективной?
а) 
,
б) 
,
в)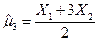 
.
Решение:
Чтобы определить, обладают ли оценки свойством несмещённости, найдём их математическое ожидание.
Таким образом, несмещёнными являются оценки и , так как их математическое ожидание равно оцениваемому параметру , оценка 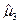не является несмещённой.
Для того, чтобы определить относительно более эффективную оценку, найдём дисперсии.
Видно, что дисперсия больше дисперсии : 
, так как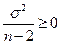 
(равенство выполняется только в том случае, когда – вырожденные случайные величины с нулевой дисперсией, в остальных случаях 
, а значит и 
).
Отсюда делаем вывод, что более эффективна оценка .
Задача 6. Метод моментов. Имеется случайная выборка X1... Xn из закона распределения, задаваемого функцией плотности:
|
|
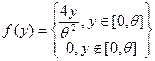
Постройте оценку параметра θ методом моментов.
Решение:
Параметр один, след, достаточно найти один первый момент.
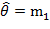=E[y] =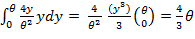 
Задача 8. Метод максимума правдоподобия.
Случайная величина Х (время безотказной работы элемента) имеет показательный закон распределения f(x) = ƛ e-ƛx (x≥0).Ниже приведено эмпирическое распределение среднего времени работы 1000 элементов (в первой строке указано среднее время xi безотказной работы одного элемента в часах; во второй строке указана частота ni – количество элементов, проработавших в среднем xi часов):
| xi | |||||||
| ni |
Найти методом максимального правдоподобия точечную оценку неизвестного параметра ƛ показательного распределения.
Решение:
Составим функцию правдоподобия:
L = f(x, θ) = П f(xi, ƛ) =П ƛ e-ƛxi = ƛn e-ƛΣxi
Найдем логарифмическую функцию правдоподобия Ln L = n lnƛ - ƛΣxi
Найдем первую производную по ƛ:
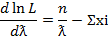
Запишем уравнение правдоподобия, для чего приравняем производную к нулю.
= 0, след ƛ = 
Найдем вторую производную по ƛ:
При ƛ =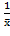 
вторая производная отрицательна, след., это и есть точка максимума.
ОТВЕТ: Находим ƛ = 1/ (20) = 0,05