Плоскость, которую пронизывает поток силовых линий, служит одновременно и некоторым "индикатором" наличия поля в данной области пространства. Однако отсутствие потока не всегда означает отсутствие поля: силовые линии могут просто "лежать" в плоскости и угол между векторами E и n составит 90 
. Дополнительным "портретом" поля, т.е.. мерой, отражающей его интенсивность и направленность, может служить в данной точке - проекция вектора Е на некоторое направление, а в пространстве плоскости - сумма произведений перемещений на проекции вектора напряженности поля на направление этих перемещений. Ближайшая механическая аналогия - подсчет работы некоторой силы. Причем в случае вектора напряженности электрического поля физический смысл аналогии сохраняется: напряженность численно равна силе, действующей на единичный заряд, а сумма произведений проекций напряженности на перемещения численно равна работе поля при перемещении единичного заряда (+1 Кл).
Рассмотрим область поля положительного точечного заряда.
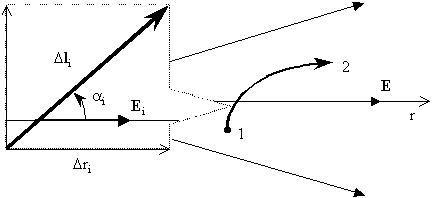
На некотором i-том участке перемещения 
l i (столь малом, что его можно считать линейным) общего перемещения единичного точечного заряда из точки 1 в точку 2 поля E в пересчете на +1 Кл совершена элементарная работа Ui, равная Е i l icos(
i). При этом l icos( i)= ri, равное проекции вектора элементарного перемещения l i на направление поля Е. При бесконечно малом перемещении
Можно сделать вывод, что при перемещении по траектории любой формы работа полем (или над полем) совершается постольку, поскольку происходит движение по силовой линии, вдоль поля (или против поля). Какой бы сложной ни была форма траектории при перемещении заряда от точки 1 в точку 2, работа в перпендикулярных силовым линиям направлениях всегда равна нулю (cos(90 )=0), а работы на "поступательно-возвратных" участках взаимно компенсируют друг друга (косинус меняет знак).
|
|
В частности при возврате в исходную точку 1 суммарная работа равна нулю: суммарная положительная работа поля компенсирована суммарной отрицательной работой внешних сил против поля. Так как замкнутая линия состоит из незамкнутых участков, то ее форма имеет более общий характер и "годится как объект для теоремы": циркуляция вектора Е вдоль замкнутой траектории тождественно равна нулю ("циркуляция" - это как раз сумма произведений перемещений на проекции вектора напряженности поля на направление этих перемещений по всей замкнутой траектории):
Пример 1. Возможна ли приведенная на рисунке ниже конфигурация электростатического поля?
Нет, невозможна. На участках обхода 2 - 3 и 4 - 1, перпендикулярных вектору поля, вклад в циркуляцию равен нулю. На участке 1 - 2 вклад положителен, на участке 3 - 4 -отрицателен, но так как на этих участках напряженность поля (густота силовых линий) различна, то суммарная циркуляция поля при обходе прямоугольника не равна 0, что противоречит теореме о циркуляции.
Пример 2. Могут ли силовые линии электростатического поля быть замкнутыми?
Нет, так как при этом циркуляция вектора поля, подсчитанная, например, вдоль силовой линии (косинус угла между вектором напряженности и направлением обхода всегда равен +1), не равна нулю.
Поля, силовые линии которых замкнуты, называются вихревыми. В них, в частности, сумма произведений вектора поля на направления обхода зависит от формы траектории, как это видно из сравнения двух траекторий от точки 1 в точку 2 на рисунке:
|
|
Независимость работы от формы траектории или нулевая циркуляция вектора поля - признак консервативности электрического поля неподвижного заряда. Ясно, что стационарные поля любых центральных (сферически симметричных) сил, например, гравитационной, являются консервативными.