Теплопроводность и теплопередача

Работа № 1

 

Условие задания: смесь идеальных газов задана мольными долями компонентов: N₂ = 65%; O₂ = 6%; Н₂ = 5 %; CO = 5%; CO₂ = 19%; H₂O = 0%. Первоначально термодинамическая система (ТДС) находится в состоянии 1 с параметрами Р₁ = 10,0 бар, t₁ = 300 ^оС. Система совершает адиабатный процесс 1-2, затем изобарный процесс 2-3 и приходит в состояние 3 с параметрами p ₃ = 4,0 бар, v ₃ = 0,3 м³/кг.

Определить: термические параметры p, v, Т состояний 1,2,3, изменение внутренней энергии, энтальпии, энтропии; работу и тепло в процессах 1-2, 2-3.

«АУЭС» каф. ТЭУ

КР-05В070200-2014

Лит

Лист

Листов

Задание

Изм.

Лист

№ докум.

Подп.

Дата Дата                     Дата

Выполнил

Абитбек А.

Проверила

Ем Т.М

Решение:

Молярные массы компонентов смеси равны:

М N₂ = 28, М О₂ = 32; М H₂ = 2; М СО = 28, М CO₂ = 44.

 

Газовые постоянные компонентов газов, Дж/кг·К,

R N₂ = 296,93; R O₂ = 259,81; R H₂ = 4124; R СО = 296,93; R CO₂ = 188,95.

Переведем объемные доли в массовые:

 

;

 

Для азота:

 

= 0,607

 

= 0,064

 

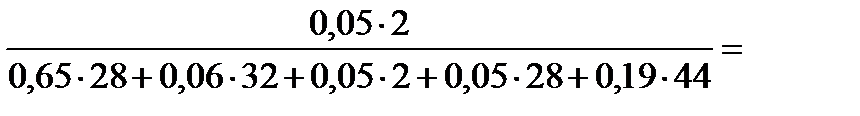= 0,0033

 

= 0,0467

= 0,279

Газовая постоянная смеси по (3.8)

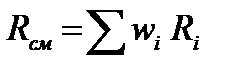= 0,607·296,93 + 0,064·259,81 + 0,0033·4124 + 0,0467·296,93 +

+ 0,279·188,95 = 277,2 Дж/кг·К.

 

Молекулярная масса смеси находится 2 способами:

а) = ;

б) По заданным х_і = φ_і , находим . Мольные доли компонентов газа по N₂ = 65 %; O₂ = 6%; H₂ = 5%; CO = 5 %; CO₂ = 19 % и объемные доли

φ_N2 = 0,65; φ_O2 = 0,06; φ_H2 = 0,05; φ_СО = 0,05; φ_СO2 = 0,19.

=0,65·28+0,06·32+ 0,05·2 + 0,05·28 + 0,19·44 = 29,98 кг/кмоль.

В пределах ошибки счета результат совпадает с предыдущим. Принимаем = 29,99 кг/кмоль.

Уравнение состояния для 1кг смеси газов имеет вид

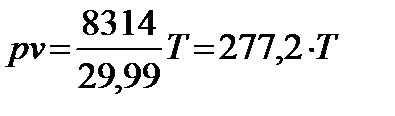
Находим значение ν ₁, Т₃ , Р₂

 

м³/кг; ν ₃ = 0,3 м³/кг

 

 

Процесс 2-3 изобарный поэтому Р₂ = Р₃ = 4,0 бар;

 

Для нахождения параметров в состоянии 2 предварительно находим показатель адиабаты к.

Представим зависимость теплоемкостей от температуры линейной функцией. Тогда по (13) получим, что средняя теплоемкость в интервале температур t₁ ÷ t₃ будет истинной теплоемкостью при средней температуре (t₁ + t₃)/2. В нашей задаче t_ср ≈ 250°С. Для температуры 250°С найдем значения средних теплоемкостей по данным [3],табл.9-12:

Компоненты смеси
N2	1,06	0,763
О2	0,978	0,719
H2	14,516	10,39
СО	1,07	0,772
СO2	1,03	0,84

Средние теплоемкости смеси газов 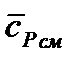, , равны

= 0,607·1,06 + 0,064·0,978 + 0,0033·14,516 + 0,0467·1,07+

 

+ 0,279·1,03 = 1,092 кДж/(кг·К)

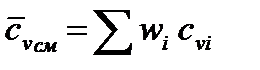= 0,607·0,763 + 0,064·0,719 + 0,0033·10,39 + 0,0467·0,772 +

+ 0,279·0,84 = 0,814 кДж/(м³·К).

 

Показатель адиабаты

 

При адиабатном процессе 1-2 из (4.24) находим параметры в состоянии 2:

 

0,314 м³/кг

 

Т₂ = Т₁· 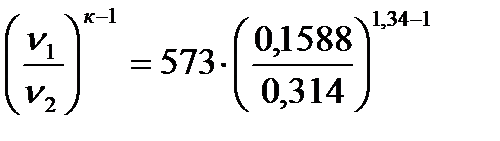= 454 К

 

Находим термические параметры состояний:

1) p ₁ = 10,0 бар, v ₁= 0,1588 м³/кг, t ₁= 300 °С;

2) p ₂ = 4,0 бар, v ₂ = 0,314 м³/кг, t ₂= 181 °С;

3) p ₃ = 4,0 бар, v ₃= 0,3 м³/кг, t ₃= 160 °С.

 

1-2 адиабатный процесс

 

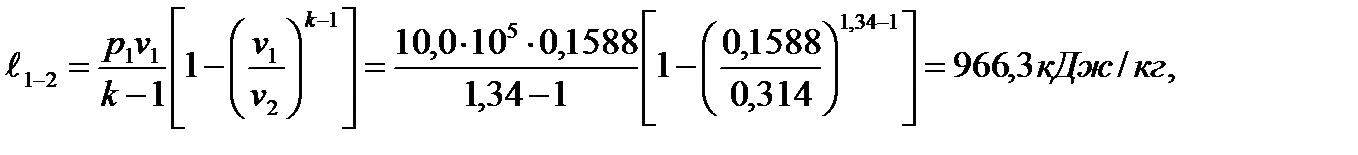
2-3 изобарный процесс

При построении термодинамических процессов в p, v; p, T; Ts - диаграммах состояний принимаем значение энтропии в состоянии 1, равной s _осм и рассчитанной для смеси газов по s _о компонентов, взятых из таблиц 13-19 [3].

 

Рисунок 1.1 – p,v –диаграмма Рисунок 1.2 - p,Т –диаграмма

 

 

 

Рисунок 1.3 - Т,s –диаграмма процессов

«АУЭС» каф. ТЭУ «АУЭС» каф. ТЭУ

КР-05В070200-2014КР-05В070200-2014

Лит     Лит

Лист   Лист

Листов   Листов

Рисунки

Изм.   Изм.

Лист     Лист

№ докум.   № докум.

Подп.   Подп.

Дата Дата                     Дата                   Дата Дата                     Дата

Выполнил   Выполнил

Абитбек А. Абитбек А.

Проверила   Проверила

Ем Т.МЕм Т.М

 

Работа № 2

 

Вода находится в состоянии насыщения при давлении р₁, бар. Насосом вода подается в парогенератор при давлении р₂, бар, где она нагревается изобарно до состояния пара со степенью сухости х₄, затем дросселируется до состояния со степенью сухости х₅. Далее пар направляется в суживающееся сопло. Состояние пара за соплом характеризуется давлением р₆, бар (см. рисунок 2.1). Принять, что все процессы являются обратимыми.

 

Рисунок 2.1 – h, s–диаграмма процесса

 

Задание

Используя «Таблицы термодинамических свойств воды и водяного пара» (далее таблицы), найти термические и калорические параметры состояний 1,2,3,4,5,6, определить интегральный дроссель-эффект в процессе 4 – 5, найти параметры пара на срезе сопла, подведенную воде и пару теплоту, скорость пара, выходящего из сопла.

Вода имеет параметры в главной тройной точке: p _тр = 610,8 Па, T_тр = 273,16 К, v _тр = 1,0002 см³/г, критические параметры: p _кр = 22,115 МПа, t _кр = 374,12 °С, v _кр = 0,003147 м³/кг.

В тройной точке принимаются значения удельных внутренней энергии и энтропии, равной нулю. Энтальпия в тройной точке h _тр = 0,611 Дж/кг, в критической точке h _кр = 2095,2 кДж/кг, s _кр = 4,4237 кДж/кг×К.

Заданы параметры пара:
р1, бар	р2, бар	х4	х5	р6, бар
0,06		0,92	0,95	0,45

«АУЭС» каф. ТЭУ

КР-05В070200-2014

Лит

Лист

Листов

Задание

Изм.

Лист

№ докум.

Подп.

Дата Дата                     Дата

Выполнил

Абитбек А.

Проверил

Ем Т.М

По таблице II при р1 =

0,06

бар, следующие параметры:

Температура, t1 =

36,18

ºС

Удельный объем, v 1 =

0,0010064

м³/кг

Энтальпия воды, h1 =

151,5

кДж/кг

Энтропия воды, s1 =

0,5209

кДж/кгК

Внутренняя энергия:

u1 = h1 - p1 ·v 1 =

145,4616

кДж/кг

Находим параметры в состоянии 2:

Давление воды, р2 =

Па

По таблице III при v 2 = v 1 =

0,0010064

м³/кг

интерполяцией находим h2 =

185,2

кДж/кг

температура, t2 =

ºС

энтропия s2 =

0,609

кДж/кгК

Состояние 3 находим на левой пограничной кривой по изобаре р2

р3 = р2 =

бар

Используем таблицу II и находим:

t3 =

275,6

ºС

v 3=

0,0013187

м³/кг

h3 =

1213,9

кДж/кг

s3 =

3,0277

кДж/кгК

параметры на правой пограничной кривой по изобаре

МПа

v "=

0,03241

м³/кг

h" =

2783,3

кДж/кг

s" =

5,8878

кДж/кгК

В состоянии 4 х4 =

0,92

t4 =

275,6

ºС

v 4= v '(1 - x4) + v "·x4 =

0,0299227

м³/кг

h4 = h'(1 - x4) + h"·x4 =

2657,748

кДж/кг

s4 = s'(1 - x4) + s"·x4 =

5,66

кДж/кгК

При адиабатном дросселировании h = const, h4 = h5 =

2657,748

кДж/кг

В состоянии 5 х5 =

0,95

По диаграмме и таблицам определяем параметры состояния

Давление

р5 =

8,0

бар

Объем

v 5=

0,24

м³/кг

Температура t5 =

ºС

Энтропии

s' =

2,0457

кДж/кгК

s" =

6,6618

кДж/кгК

Энтропия

s5 = s'(1 - x5) + s"·x5 =

6,430995

кДж/кгК

 

 

энтальпии	h' =	720,9	кДж/кг	h" =	2768,4	кДж/кг
Энтальпия расчетная	h5расч = h'(1 - x5) + h"·x5 =	2666,025	кДж/кг
Интегральный дроссель-эффект
	t5 - t4 =	-105,6	ºС
Тепло подводится в парогенераторе по изобаре 2 - 3 - 4
	q2-4 = h4 - h2 =	2472,548	кДж/кг
Работа насоса
	ℓн = h2 - h1 =	33,7	кДж/кг
Состояние влажного пара в точке 6 по hs-диаграмме
при р6 =	0,45	бар	и s = s5 =	6,430995	кДж/кгК
v 6=		м³/кг
h6 =	2220,0	кДж/кг
x6 =	0,82
По таблицам при р6 =	0,45	бар
s' =	1,06	кДж/кгК
s" =	7,6234	кДж/кгК
	x =(s5 - s')/(s" - s') =	0,8183251
Находим параметры:	t6 =	78,7	ºС
		h' =	329,65	кДж/кг
		h" =	2641,5	кДж/кг
		h6 =	2221,495	кДж/кг
		v '=	0,0010287	м³/кг
		v "=	3,580	м³/кг
		v 6=	0,0031165	м³/кг
По изоэнтропе 5-6 выбираем два состояния:
v 1=	0,39	м³/кг	р1 =	5,0	бар	0,585
v 2=	0,78	м³/кг	р2 =	2,0	бар
По этим параметрам находим скорость звука: а =	513,079	м/с
Использованный теплоперепад	∆h = a ² /2 =	131,63	кДж/кг
Состояние пара на срезе сопла по значениеям s и h
hc = h5 - ∆h =	2526,12	кДж/кг
v c=	0,42	м³/кг;	pc =	4,0	бар;
t6 =	143,62	ºС

 

 

Рисунок 5.2 – HS диаграмма

«АУЭС» каф. ТЭУ

КР-05В070200-2014

Лит

Лист

Листов

Рисунки

Изм.

Лист

№ докум.

Подп.

Дата Дата                     Дата

Выполнил

Абитбек А.

Проверила

Ем Т.М

Работа № 3

 

№_з.к.: 121099 (m=9 n=9)

 

Теплопроводность и теплопередача

 

Задание 3.1. Определение коэффициента теплопроводности тел градиентным методом.

Рисунок 3.1   Рисунок 3.1

Опытный образец выполнен в виде цилиндрического диска радиуса r =10 мм и толщины δ=1 мм. Он плотно размещен между равномерно нагретым до температуры t₁ =120 + m + 0,2n = 128.4 °С и холодным с температурой t₂ = 20 + 0,1n = 20.2 °С полюсами прибора. Благодаря теплозащитным нагревателям, радиальные потери тепла отсутствуют (см. рисунок 3.1).

Определите значение коэффициента теплопроводности образца (исследуемого материала) λ при стационарном тепловом потоке Q = 23,2 Вт через образец.

«АУЭС» каф. ТЭУ

КР-05В070200-2014

Лит

Лист

Листов

Задание

Изм.

Лист

№ докум.

Подп.

Дата Дата                     Дата

Выполнил

Абитбек А.

Проверила

Ем Т.М

Решение варианта m = 9 n = 9. Из формулы теплоты теплопроводности (1.1.28)

 

Q = , Вт

F = πr²

находим значение коэффициента теплопроводности образца

 

 

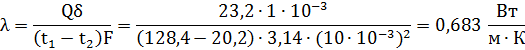
Ответ для варианта m = 9 n = 9, λ = 0,683 Вт/(м К).

 

Задание 3.2. Теплопередача (1.20 [3]).

Обмуровка печи выполнена из слоя шамотного кирпича с коэффициентом теплопроводности

λ(t) = 0,84(1 + 0,695 10 ³10^-3 t) = λ₀(1 + в t), Вт/(м К),

Рисунок 3.2   Рисунок 3.2

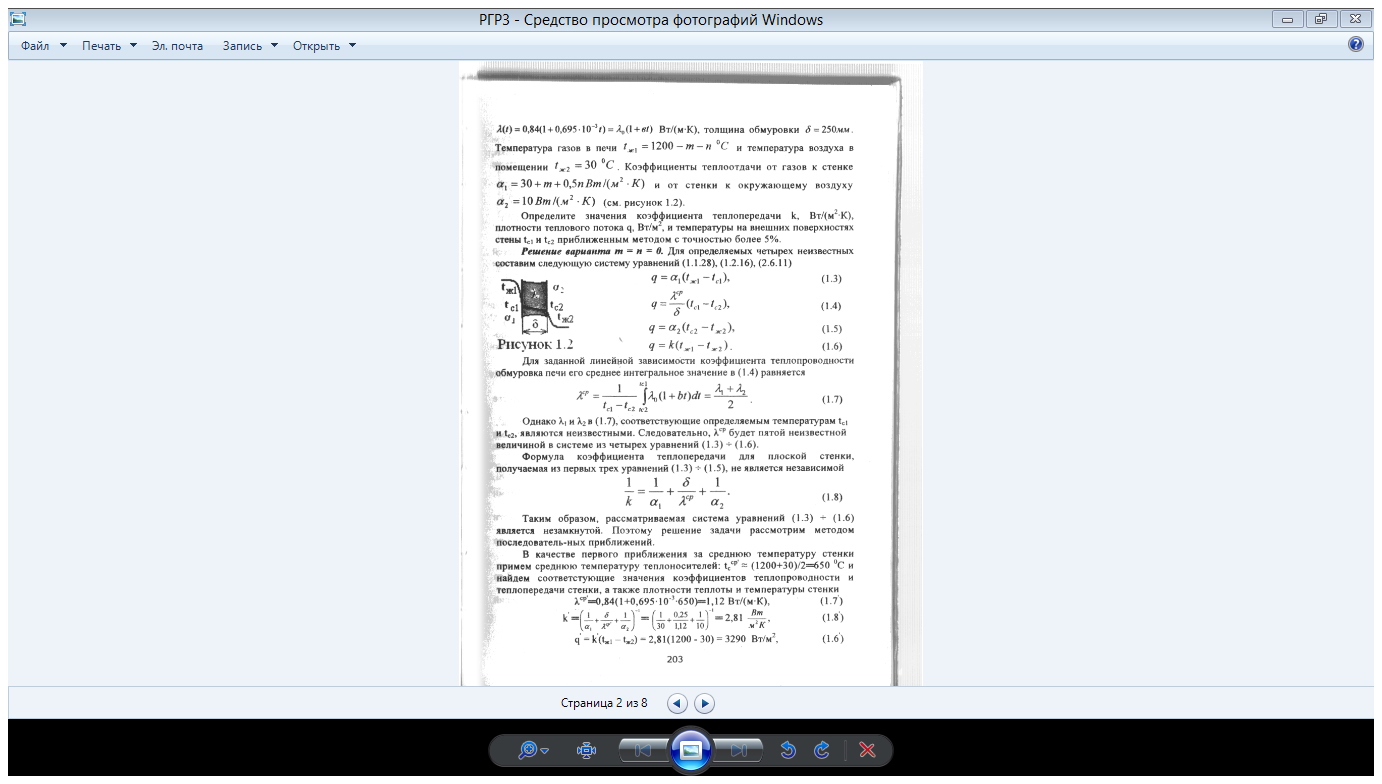толщина обмуровки δ = 250мм. Температура газов в печи t_ж1 =1200 —m — n =1190 °С _и температура воздуха в помещении t_ж2 = 30 °С. Коэффициенты теплоотдачи от газов к стенке α₁ =30 + m + 0,5n = 39 Вт/(м² К) и от стенки к окружающему воздуху

α₂ =10 Вт/(м² К) (см. рисунок 3.2).

Определите значения коэффициента теплопередачи k, Вт/(м²К), плотности теплового потока q, Вт/м², и температуры на внешних поверхностях стены t_c1 и t_c2 приближенным методом с точностью более 5%.

Решение варианта m = 9, n = 9. Для определяемых четырех неизвестных составим следующую систему уравнений

 

q=α₁(t_ж1 – t_с1)

q= (t_c1 – t_c2)

q=α₂(t_c2 – t_ж2)

q=k(t_ж1 – t_ж2)

 

Для заданной линейной зависимости коэффициента теплопроводности обмуровка печи его среднее интегральное значение равняется

.

Однако λ₁и λ₂, соответствующие определяемым температурам t_c1 и t_c2, являются неизвестными. Следовательно, λ^ср будет пятой неизвестной величиной в системе из четырех уравнений.

Формула коэффициента теплопередачи для плоской стенки, получаемая из первых трех уравнений, не является независимой

 

 

Таким образом, рассматриваемая система уравнений является незамкнутой. Поэтому решение задачи рассмотрим методом последовательных приближений.

В качестве первого приближения за среднюю температуру стенки примем среднюю температуру теплоносителей: t_c^cp’ ≈ (1190+30)/2=610 °С и найдем соответствующие значения коэффициентов теплопроводности и теплопередачи стенки, а также плотности теплоты и температуры стенки

 

λ^ср’=0,84(1+0,695∙10^-3∙610)=1,196 Вт/(м К),

[Вт/(м²К)]

q^’ = k’(t_ж1 – t_ж2) = 2,988(1190 – 30) = 3466 Вт/м²

t_c1‘ = t_ж1 – q'/α₁ = 1190 – 3466/39 = 359 °C

t_c2‘ = t + q'/α₂ = 30 + 3466/10 = 376,608 °C.

 

Во втором приближении значения средней температуры стенки, коэффициентов теплопроводности и теплопередачи стенки, а также плотности теплоты будут следующими

 

t_c^cp’’ ≈ (1101,1262+376,608)/2=738,8671 °С

λ^ср’’=0,84(1+0,695∙10^-3∙738,8671)=1,271 Вт/(м К),

[Вт/(м²К)]

q^’’ = k’’(t_ж1 – t_ж2) = 3,102(1190 – 30) = 3598,32 Вт/м²

 

При этом значении плотности теплоты температуры поверхностей стенки, средняя температура стенки и соответствующее ей значение коэффициента теплопроводности для третьего приближения будут равны

 

t_c1" = t_ж1 - q''/α₁, =1190 – 3598,98/30 = 1097,74 °С,

t_c2" = t_ж2 + q''/α₂= 30 + 3598,98/10 = 389,832 °С,

t_c^cp"'= (t_с1" + t_c2'')/2 =(1097,74 + 389,832)/2 = 743,79 °C,

λ^{ср’’’}=0,84(1+0,695∙10^-3∙743,79) = 1,274 Вт/(м К),

 

В третьем приближении среднее значение коэффициента теплопроводности изменилось очень мало, то есть точность его вычисления намного выше, чем заданная

 

< 5%

 

В качестве ответов можно принять результаты второго приближения:

t_c1 = t_c1" = 1097,74 °C, t_c2 = t_c2" = 389,832 °С, k = k" = 3,102 Вт/(м² К), q = q" = 3598.32 Вт/м².

 

Задание 3.3. Определение коэффициента теплопроводности жидкости метод нагретой нити.

Рисунок 3.3   Рисунок 3.3

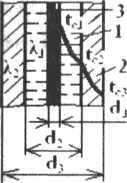В приборе для определения коэффициента теплопроводности жидкостей по методу «нагретой нити» (см. рисунок 3.3) в кольцевой зазор 1 между платиновой нитью 3 и кварцевой трубкой 2 залито испытуемое масло 1. Диаметр и длина платиновой нити d₁ = 0,12 и 1 = 90 мм; внутренний и наружный диаметры кварцевой трубки d₂ = 1 и d₃ = 3 мм; коэффициент теплопроводности кварца λ₂ = 1,4 Вт/(м К).

Вычислите коэффициент теплопроводности λ₁ и среднюю температуру t₁^ср масла, если при расходе тепла через кольцевой слой масла Q = 1,8 + 0,1m + 0,1 n = 2,8 Вт, температура платиновой нити t_с1 = 106,9 + m + 0,2n = 115,3 °С и температура внешней поверхности кварцевой трубки t_с3 = 30,6 °С.

Решение варианта m = 8 n = 2. Опытный участок представляет собой двухслойную цилиндрическую стенку, для которой формула теплового потока Q теплопроводностью имеет вид

 

 

Отсюда, искомое значение λ₁ с учетом исходных данных определяется следующим образом

 

 

 

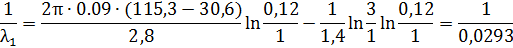
Среднюю температуру t₁^Cр трансформаторного масла (как температуру отнесения полученного значения его коэффициента теплопроводности λ₁ = 0,0293 Вт/(м∙К)) найдем приблизительно как среднее значение температур окружающих его стенок

 

, t_c2= t_с3+ 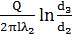=30,6 + = 34,4875°С

 

t₁^ср= (t_с1 + t_c2)/2 = (115,3 + 34,4875)/2 = 74,89 °С.

 

Ответ для варианта m = 8 n = 2 λ₁ = 0,0293 Вт/(м К), t₁^ср = 74,89 °С.

 

Задание 3.4. Критический диаметр.

Рисунок 3.4   Рисунок 3.4

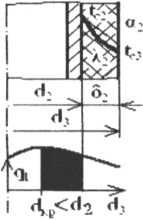Необходимо теплоизолировать трубопровод с наружным диаметром d₂ = 200 + m + n = 210 мм и температурой наружной поверхности t_с2 = 130 + m + 0,1 n = 138,2 °С, которую можно принять такой же и после наложения изоляции. Пусть температура на внешней поверхности изоляции и линейная плотность тепловые потери не превышают t_c3<30°C и q_i < 200 Вт/м. Коэффициент теплоотдачи от внешней поверхности изоляции к окружающему воздуху α₂ = 10 + m + 0,2 n = 18,4 Вт/(м²К) (см. рисунок 3.4).

Целесообразно ли выбрать в качестве тепловой изоляции материал с коэффициентом теплопроводности λ₂ = 0,05 + 0,1m + 0,1 n = 1,05 Вт/(м К)? Если целесообразно, то какой толщины δ₂ должен быть слой этого теплоизоляционного материала?

Решение варианта m = 9 n = 9. Критический диаметр цилиндрической стенки в предположении α₂ (d₃) = пост определяется следующим образом

Bi = 2; α₂∙d_кр /λ_кр≈2; d_кр^:=2λ₂/α₂ ≈ 2∙1,05/18,4= 0,114м = 114 мм. В данном случае d_кр = 114 мм < d₂ = 210 мм и согласно графическому изображению процесса на рисунке 1.4 применение данного (с λ₂ = 1,05 Вт/(м К)) теплоизоляционного материала (в рассмотренных условиях q_l < q_l^max) приводит к снижению тепловых потерь, следовательно, целесообразно.

При целесообразности использования теплоизоляционного материала, заданного значением коэффициентом теплопроводности, следует определить толщину его слоя δ₂, необходимую для выполнения условий задачи о допустимых значениях плотности тепловых потерь и температуры наружной поверхности изоляции. Для этого используется формула линейной плотности тепловых потоков стационарной теплопроводности

 

q₁=Q/l = 2πλ₂(t_c2-t_c3)ln(d₂/d₃).

 

При этом заметим, что для предварительной оценки удобно пользоваться ее более простым приближенным видом, обеспечивающим при d₃/ d₂<2 точность расчета более 4% путем замены логарифма первым слагаемым его разложения в ряд (ln(d₂/d₃) = d₂/(2δ₂))

q₁ |_d3≤2d2≈ 2πλ₂(t_c2 —t_c3)d₂ /(2δ₂).

 

Согласно приближенной формуле

δ₂ ≈ πλ₂d₂(t_c2 - t_c3)/q₁ = π1,05∙0,21(138,2-30)/200 = 0,375м= 375мм.

Проверка условия приближенного вычисления

d₃^≈ = d₂ + 2δ₂ ≈ 210 + 2∙0,375 = 960 мм; d₃^≈ /d₂ = 231,4/200 = 4,57 > 2 показывает, что она выполняется и можно было бы приближенно принять δ₂ = 375 мм. Однако ошибки приближенных вычислений, как известно, накапливаются и поэтому результаты их могут приняты как оценочные, а реально использоваться, если только удовлетворяют они допустимым их значениям. В данном случае приближенное (по d₃^≈) расчетное значение плотности тепловых потерь, но определяемое по строгой формуле

 

q₁^≈расч/q₁^зад = 2πλ₂(t_c2 - t_c3)ln(d₂/d₃^≈)/q₁=2π1,05∙108,2ln(210/960)/200 =1.42

 

превышает заданное ее значение на 4.2 %, что ниже принятой (по умолчанию) точности рассмотренного приближенного метода, а именно 4 %.

Поэтому принимаем δ₂ = 375 мм как оценочный результат и определяем толщину слоя теплоизоляционного материала по строгой формуле, следующим образом ln(d₃/d₂)=2πλ₂(t_c2-t_c3)/q₁=2π∙1,05∙108.2/200=3.57, d₃/d₂ = 1,17, d₃= 1,17d₂ = 1,17∙210 = 245,7 мм; δ₂=(d₃-d₂)/2 = (245-210)/2 = 18 мм. (1.18)

 

Ответ для варианта m = 9 n = 9 применение данного варианта теплового изоляционного материала целесообразно, и достаточная его толщина равняется 18 мм.

 

Задание 1.5. Определение истинной температуры среды.

Температура воздуха в резервуаре измеряется ртутным термометром, который помещен в гильзу (стальную трубку), заполненную маслом (с. рисунок 1.5). Термометр показывает температуру конца гильзы t₁= 84 + 0,2m + 0,1n = 85,8 °С.

Как велика ошибка измерения за счет отвода тепла по гильзе путем теплопроводности, если температура у основания гильзы t_o=40°C, длина гильзы l = 120 + m + 0,1n = 128,2 мм, толщина гильзы δ = 1,5 ™, коэффициент теплопроводности материала гильзы λ = 55,8 – m = 47,8 Вт/(м К) и коэффициент теплоотдачи от воздуха к гильзе α = 23,3 + 0,1m = 23,5 Вт/(м²К).

Рисунок 4.5   Рисунок 4.5

Решение варианта m = 9 n = 9. Для решения воспользуемся приближенной формулой для стержня конечной длины

 

Где m = – параметр дифференциального уравнения теплопроводности стержня, м^-1;

u = πd- периметр гильзы;

f = πdδ – сечение гильзы, м².

Отсюда u/f ≈ 1/δ, m = , ml = 18,104 • 0,128 = 2,317, ch (2,317,0) = 5,1219, следовательно, , =96,89 °C.

 

Ответ для варианта m = 9 n = 9: Истинная температура воздуха t_ж = 96,89°С, ошибка измерений t_ж – t₁ = 100 - 84 = 11,09 °С.

Список литературы

 

1. Кириллин В.А., Сычев В.В. Техническая термодинамика. –М.: Энергоатоиздат. 1983.-416с.

2. Ривкин С.Л., Александров А.А. Термодинамические свойства воды и водяного парам –М.: Энергоатомоиздат, 1984 -80с.

3. Сборник задач по технической термодинамике: Уч. Пособие/ Т.Н. Андрианова идр. –М.: Изд. МЭИ, 00-356с.

4. М. И. Пак, В. П. Дубовик, Т. М. Ем.Техническая термодинамика. Расчет термодинамических процессов и теплосиловых циклов. - Алматы: АИЭС, 2008.- 34с.

5. Темирбаев Д.Ж. Тепломассообмен: Учебное пособие для вузов. –Алматы: TST-company, 2009.-251c.

 

«АУЭС» каф. ТЭУ

КР-05В070200-2014

Лит

Лист

Листов

Список литературы

Изм.

Лист

№ докум.

Подп.

Дата Дата                     Дата

Выполнил

Абитбек А.

Проверила

Ем Т.М