МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ
РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧЕРЕЖДЕНИЕ ВЫСШЕГО
ОБРАЗОВАНИЯ
СТЕРЛИТАМАКСКИЙ ФИЛИАЛ БАШКИРСКОГО
ГОСУДАРСТЕННОГО УНИВЕРСИТЕТА
РЕФЕРАТ
по дисциплине «Дискретная математика»
на тему: «Теория множеств»
Выполнил: студент
Дорофеев И.В.
ПМИ21
Проверил: доц.
Акимов А.А.
Стерлитамак 2021 г.
Содержание
1. Введение………………………………………………………………….3
2. История становления теории множеств.……………………………….4
3. Основные определения ………………………………….……………...6
4. Заключение………………………………………………………………9
5. Список литературы……………………………………………………..10
Введение
Впервые мы знакомимся с термином «множества» в начальной школе. Например, при изучении совокупности чего-либо: множество животных, людей в помещении, положительных и отрицательных чисел. В средней школе были изучены некоторые свойства и действия над множествами, бесконечные и конечные множества, области определения и значения функции как пример множеств и т.д.
В математике постоянно приходится иметь дело с различными множествами: множество точек на прямой, прямых на плоскости, плоскостей в пространстве и т.д. Роль, которую понятие множества играет в современной математике, определяется не только тем, что сама теория множеств стала в настоящее время весьма обширной и содержательной дисциплиной, но главным образом тем влиянием, которое теория множеств, возникшая в 70-х годах XIX века, оказывала и оказывает на всю математику в целом.
Поэтому, в данном работе, прежде чем приступить к описанию основных положений теории множеств были рассмотрены основные этапы ее становления.
История становления теории множеств
Зачастую создание теории множеств сравнивают с революционным переворотом, равнозначным признанию математики дедуктивной наукой в древней Греции, разработке теории классического математического анализа или появление неевклидовой геометрии.
Несомненным родоначальником теории множеств нужно назвать немецкого математика Георга Кантора. Кто-то может поспорить, что понятием множеств пользовались в математике еще со времен Древней Греции, но там они использовались в неявной форме и четкого представления о теории множеств не были сформулированы четко и лаконично. Также первые представления о «актуально бесконечном множестве» можно увидеть в работах Гаусса начала 1800-х годов, где происходят сравнения на множестве рациональных чисел, обнаруживаются классы эквивалентности и разбивается все множество на эти классы. Но и тут бесконечные множества не были объектом исследования, тем более, что Гаусс выступал против использования множеств в математических доказательствах.
Наиболее близки к теории множеств Кантора были труды чешского математика Бернарда Больцано. Так в его труде «Парадоксы бесконечного» 1851 г. рассматриваются произвольные числовые множества, вводится понятие взаимно-однозначного соответствия. Но и здесь его работа носит философский характер и к математике к которой мы привыкли не имела никакого отношения.
И только Кантор в 1870 году разработал программу стандартизации математики и любой математический объект предложил рассматривать как некоторое множество. Тем самым сделал понятие «множество» объектом исследования. В 1879-1884гг. он публикует шесть статей с результатами исследований бесконечно точечных множеств.
Наконец, в 1895–1897 годах Кантор дал систематизированное изложение своих трудов и положил теорию множеств в фундамент всей математики.
Таким образом, Георг Кантор является родоначальником теории множеств. Эту теорию называют «наивной» из-за размытости понятия множества. Благодаря этой нечеткой формулировки в период 1895-1925гг. были обнаружены противоречия, которые внесли большое количество сомнений в использовании этой теории как основы для всей математики.
Изучая наивную теорию множеств, британский математик Бертран Рассел нашел противоречие, которое впоследствии получило название парадокс Рассела. Формулировка: пусть А — множество всех множеств, которые не содержат себя в качестве своего элемента. Содержит ли А само себя в качестве элемента? Если да, то, по определению А, оно не должно быть элементом А — противоречие. Если нет — то, по определению А, оно должно быть элементом А — вновь противоречие.
Таким образом, была показана несостоятельность наивной теории множеств. После этого сообщество математиков поделилось на два лагеря: одни пытались доказать правильность наивной теории множеств, другие полностью от нее отказались (например, Л. Э. Я. Брауэр и его школа).
Первые во главе с немецким математиком Д. Гильбертом разработали различные аксиоматизации теории множеств.
Аксиоматизация основана на отказе от существования множества в некотором идеальном мире. В рамках этой теории свойства понятия множества зависит от выбора аксиом, на которые она опирается. Это дало возможность для второго лагеря математиков критиковать эту теорию.
В наши дни распространенной аксиоматической теорией является теория Цермело-Френкеля, основанной на аксиоме выбора.
Основные определения
Понятие множество настолько обширно, что сформулировать его четкое определение практически невозможно. При первых же попытках вы столкнётесь с проблемой. Например, дадим следующее определение: множество — это какая-то совокупность предметов (объектов) произвольной природы. То есть определение множества дается через синоним (в данном случае это совокупность). Понятие множество является основным понятием математики и его нельзя определить через другое. В наших силах лишь пояснить его на примерах.
Множества принято обозначать прописными латинскими буквами: A, B, …, а его элементы строчными латинскими буквами: a, b, ….
Если элемент х принадлежит множеству А, то пишут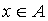 
.
Если же элемент х не принадлежит множеству А, то пишут 
.
Тогда встает вопрос, а как можно описать или задать множество. Говорят, что множество задано, если известно какие элементы принадлежат этому множеству, а какие нет.
Известны два способа описания множества.
Первый из них очень прост: перечисли все элементы множества. При таком задании множества все его элементы записываются в строку через запятую и заключаются в фигурные скобки.
А={1,3,5,7,9,11,13}. (1)
Второй способ сложней, но компактней: при записи множества укажите его характеристическое свойство. Характеристическое свойство – это такое свойство, которым обладает каждый элемент, принадлежащий множеству, и не обладает ни один элемент, который ему не принадлежит.
A={a | aÎN,a>100}. (2)
Посмотрев на приведенные примеры можно увидеть, что множества имеют как конечное, так и бесконечное число элементов. Поэтому выделяют два вида множеств — конечные и бесконечные.
Также, множество, которое не содержащее ни одного элемента называют пустым и обозначается оно символом: Æ.
Еще одно важное понятие в рассматриваемой теории это понятие подмножества.
Множество В будем называть подмножеством множества А лишь только в том случае, если любой элемент множества В является элементом множества А. вводят следующее обозначение BÌ A.
Введем еще одно понятие, которое удобно для применения. Это универсальное множество. Универсальным, называют такое множество, которое включает все рассматриваемые множества. Обозначение — U.
Нарисуем замкнутый контур и представим, что это некоторое множество А. Тогда все точки которые лежат внутри данного контура являются элементами множества А. такое графическое представление множества удобно для применения и носит название диаграмм Эйлера-Венна. Универсальные множества принято изображать прямоугольником, а результат операций штриховкой.
| В |
| А |
Давайте разберем как могут вести себя два множества относительно друг друга.
Если два множества не имеют одинаковых элементов, то говорят, что эти множества находятся в отношении непересечения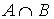 
=Æ.
Если два множества имеют одинаковые элементы, то говорят, что эти множества находятся в отношении пересечения 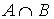≠ Æ
Если все элементы одного множества являются элементами другого, то говорят, что два множества находятся в отношении включения.
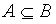(А содержится в В или В включает А), если 
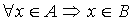А называется подмножеством В. Есл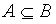и и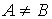 
, то А называется строгим (собственным) подмножеством В. Обозначается это 
.
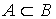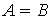если они являются подмножествами друг друга, то есть 
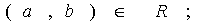или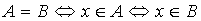 
Это всего лишь малая часть понятий, которыми оперирует теория множеств.
Заключение
Современная математика не представляет себя без такого понятия как множество. Оно является одним из основополагающих. Уникальность этого понятия в том, что под него можно подвести любую совокупность объектов, явлений и предметов. Причем сами множества объединяются в другие множества и рассматриваются как отдельные объекты.
Все содержание понятия множества можно вполне описать словами синонимами: совокупность, общность, набор и т.д. Поэтому дать строгое определение понятию множества трудно. Скорее всего это связано с тем, что долгое время это понятие носило более философский характер, чем математический.
Что же касается самой теории множеств, то она прошла не легкий путь становления. Как и любая теория изначальна она содержала противоречия, которые всем известны как парадоксы (парадоксы Кантора, Рассела и др.). Но с помощью аксиом теории множеств многие были преодолены.
Теория множеств решает множества задач современной математики и лежит в ее основе.
Список литературы
1. Дискретная математика для программистов / Ф.А.Новиков. – СПб.: Питер, 2002. – 304 с.
2. Жолков С.Ю. Математика и информатика для гуманитариев: Учебник. – М.: Гардарики, 2002. – 531 с.
3. Судоплатов С.В., Овчинникова Е.В. Элементы дискретной математики: Учебник. – М.: ИНФРА-М, Новосибирск: Изд-во НГТУ, 2002. – 280 с. – (Серия «Высшее образование»)
4. Материал из Википедии — свободной энциклопедии. Георг Кантор (https://www.peoples.ru/science/mathematics/kantor/)