Раздел 3. Обеспечение учебных занятий
 
3.1. Методическое обеспечение
3.1.1 Методические указания по освоению дисциплины
Методическое обеспечение дисциплины осуществляется за счет использования современных учебников (учебных комплексов, справочной литературы, интернет-сайтов специальных изданий, организаций) и учебных пособий по дисциплине «Математические методы в психологии», а также компьютерные программы Excel и IBMSPSS. Для проведения занятий по данной дисциплине используются следующие методы и инновационные технологии обучения: - презентации материалов, - выполнение практических заданий на компьютере под руководством преподавателя; - самостоятельное решение практических заданий по анализу данных на компьютере.
3.1.2 Методическое обеспечение самостоятельной работы
Задания для самостоятельной работы 1. Построить гистограмму, преобразовать данные из шкалы в шкалу, вычислить описательные статистики: моду, медиану, среднее, процентили, дисперсию, стандартное отклонение, z-значения. 2. По таблице стандартных нормальных вероятностей определить вероятность встречаемости значений в заданном диапазоне шкалы с заданным средним и стандартным отклонением. 3. Проверить нормальность распределения с применением критериев асимметрии и эксцесса. 4. Сформулировать содержательные психологические гипотезы, представить их на языке статистики, выбрать соответствующие критерии и проверить статистические гипотезы, записав выводы по результатам проверки каждой гипотезы: - с применением критерия t-Стьюдента для независимых выборок (с предварительной проверкой равенства дисперсий; - с применением критерия t-Стьюдента для зависимых выборок; - с применением критерия U Манна-Уитни; - с применением критерия T Вилкоксона; - с применением критерия Хи-квадрат Пирсона; - с применением критерия Н Краскала-Уоллеса; - с применением критерия Хи-квадрат Фридмана; - с применением корреляции Пирсона; - с применением корреляции Спирмена и Тау-Кендалла. 5. Применить однофакторный дисперсионный анализ с предварительной проверкой гомогенности дисперсии, с последующим множественным сравнением средних Post Hoc и методом контрастов. 6. Применить двухфакторный дисперсионный анализ и проинтерпретировать его результаты. 7. Применить многомерный дисперсионный анализ и проинтерпретировать его результаты. 8. Применить дисперсионный анализ с повторными измерениями и проинтерпретировать его результаты. 9. Интерпретация результатов множественного регрессионного анализа. 10. Определение последовательности и интерпретация результатов факторного анализа. Файлы примеров для практических занятий и самостоятельной работы представлены на сайтах преподавателей.
3.1.3 Методика проведения текущего контроля успеваемости и промежуточной аттестации и критерии оценивания
Для сдачи зачета необходимо: 1) ответить на вопросы теста, состоящего из двух частей: - часть 1: 10 вопросов из пунктов 1 - 54 (см. п. 3.1.4.), - часть 2: 10 вопросов из пунктов 55 – 112 (см. там же); 2) решить 1 практическую задачу из перечисленных в п. 4 (см. п. 3.1.2.). Требования к сдаче зачета: не менее 6 правильных ответов по каждой из двух частей теста и правильное решение практической задачи.   Для сдачи экзамена необходимо: 1) ответить на вопросы теста, состоящего из трех частей: - часть 1: 10 вопросов из пунктов 1 - 54 (см. п. 3.1.4.), - часть 2: 10 вопросов из пунктов 55 – 112 (см. там же), - часть 3: 10 вопросов из пунктов 113 – 163 (см. там же); 2) решить 1 практическую задачу из заданий п. 4 и 1 практическую задачу из п. 5 – 10 (см. п. 3.1.2).  
3.1.4 Методические материалы для проведения текущего контроля успеваемости и промежуточной аттестации (контрольно-измерительные материалы, оценочные средства)
Перечень тестовых вопросов к экзамену по курсу «Статистические методы и математическое моделирование в психологии» К каждому вопросу предлагается 4 варианта ответа, из которых один является верным. Для каждого вопроса необходимо указать только одну букву, соответствующую правильному ответу на этот вопрос. Пример вопроса и вариантов ответа Такое значение переменной, измеренной на выборке испытуемых, меньше которого имеют ровно половина этих испытуемых, называется… а) мода; б) среднее; в) медиана; г) промежуточное Правильный ответ: в) медиана   1) Две выборки являются зависимыми, если 2) Гипотеза исследования это утверждение о связи двух явлений… 3) Если 1-я выборка – сотрудники администрации, а 2-я выборка – рядовые сотрудники того же предприятия, то 2-я выборка по отношению к 1-й является 4) Основной способ обеспечения репрезентативности выборки относительно генеральной совокупности это 5) Основное свойство выборки, определяющее ее качество – это: 6) Числа, обозначающие номера испытуемых в списке – это измерение в шкале… 7) Упорядочивание испытуемых по времени решения тестовой задачи – это измерение в шкале… 8) Время простой сенсомоторной реакции (в мс) – это измерение в шкале 9) Кодирование испытуемых по воинскому званию (лейтенант, капитан, майор…) для оценки должностного статуса – это измерение в шкале… 10) Одна из перечисленных характеристик не относится к шкалам (уровням) измерения С.Стивенса: 11) Для деления выборки на несколько независимых выборок обычно используется следующая переменная: 12) В качестве группирующей переменной, делящей выборку на несколько независимых групп используется: 13) Если по времени решения тестовой задачи трем испытуемым (из 20) присвоены ранги 1 (самый быстрый), 2, 5, то справедливо следующее утверждение: 14) Если по ранговой шкале тревожности трое испытуемых (из 20) имеют значения 3, 6, 9, то справедливо следующее: 15) Мода как мера центральной тенденции не пригодна для переменных в следующих шкалах: 16) Медиана как мера центральной тенденции не пригодна для переменных в следующих шкалах: 17) Среднее как мера центральной тенденции не пригодна для переменных в следующих шкалах: 18) Графики распределения частот значений признака для группы юношей (1) и группы девушек (2). Как соотносятся средние значения и дисперсии признака групп (по графику): 19) Абсолютная величина каждого отдельного значения не учитывается для определения значений следующих мер центральной тенденции: 20) Выбросы (экстремальные значения) не влияют на следующие меры центральной тенденции: 21) Если для выборки численностью 200 чел., 60-й процентиль некоторого признака равен 6, то справедливо следующее утверждение: 22) Такое значение переменной, измеренной на группе испытуемых, меньше которого имеют ровно половина этих испытуемых, называется… 23) 50-й процентиль соответствует: 24) Чему равна медиана ряда значений 1, 2, 2, 2, 3, 7, 6, 5, 9, 5: 25) Как соотносятся меры центральной тенденции для данного ряда значений 0, 0, 2, 2, 6, 6, 6, 5, 9: 26) Как соотносятся дисперсии двух рядов чисел: 27) Как соотносятся стандартные отклонения времени решения одной и той же задачи для одной и той же выборки (N = 20), выраженные в секундах и минутах: 28) Как соотносятся стандартные отклонения возраста выборки детей 2-6 лет (N = 30), выраженные в годах и месяцах: 29) Чему равна сумма отклонений выборочных значений от выборочного среднего? 30) В группах 1 и 2 измерена некоторая переменная. D1 = D2=10, M1=20, M2=30. После объединения этих групп дисперсия… 31) Если распределение переменной соответствует нормальному виду, то 90% всех ее значений находится: 32) Если распределение признака соответствует нормальному виду, то 99% всех ее значений находится: 33) Если распределение переменной соответствует нормальному виду, то 90% всех ее значений находится: 34) Если распределение переменной соответствует нормальному виду, то в диапазоне М 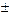1,96σ: 35) Если распределение переменной соответствует нормальному виду, то 95% всех ее значений находится: 36) Некоторое свойство измеряется при помощи тестовой шкалы CEEB (М=500, s=100). Какая приблизительно доля генеральной совокупности имеет балл от 600 до 700? 37) Некоторое свойство измеряется при помощи тестовой шкалы Бине (М=100, s=16). Какая приблизительно доля генеральной совокупности имеет балл ниже 84? 38) Для изучения каких связей коэффициенты корреляции не применимы 39) Если коэффициент корреляции Пирсона r = – 0,5, то коэффициент детерминации равен: 40) Если y – зависимая, а x – независимая переменные, то R2xy (коэффициент детерминации) это часть дисперсии… 41) Если y – зависимая, а x – независимая переменные, то R 2xy (коэффициент детерминации) равен соотношению дисперсии… 42) После z-преобразования выборочных значений переменной среднее и сигма… 43) Если Rxy=1 и обе переменные xiи yi представлены в z-значениях, то уравнение регрессии ŷi=bxi+a принимает вид: 44) Если Rxy=0, то уравнение регрессии ŷi=bxi+a принимает вид: 45) Если Rxy= 0, и обе переменные xiи yi представлены в z-значениях, то уравнение регрессии ŷi=bxi+a принимает вид: 46) Если объем выборки N=21, ковариация между двумя признаками Cov12=8, а стандартные отклонения s1=4; s2=8, то коэффициент корреляции R12 Пирсона равен 47) Если изучается взаимосвязь между двумя признаками (s1=5; s2=6; N = 21), то величина ковариации (Cov12) может быть: 48) Какая корреляция основана на подсчете разности рангов 49) Какая корреляция основана на подсчете произведений отклонений от средних 50) Какая корреляция основана на подсчете пар испытуемых: 51) Коэффициент корреляции Спирмена основан на подсчете… 52) Если при переборе всех пар испытуемых в выборке вероятность однонаправленного изменения X и Y (совпадений) составила Р = 0,8, то величина τ-Кенделла равна: 53) Если при переборе всех пар испытуемых в выборке вероятность разнонаправленного изменения X и Y (инверсий) составила Q = 0,8, то величина τ-Кенделла равна: 54) При подсчете τ -Кенделла на выборке N = 6 число совпадений составило P=10; τ –Кенделла равно… 55) Чему равна корреляция Пирсона (в других вопросах - Спирмена, Тау-Кендалла) для двух переменных:
№ X Y а) меньше 0, но больше -1 б) -1 в) 1 г) больше 0, но меньше 1
     
     
     
     
     

56) Проверяемая содержательная (научная) гипотеза подтверждается, если (при a = 0,05):

57) Если по результатам статистической проверки научной (содержательной) гипотезы (при a = 0,05) оказалось, что p < 0,05, то эта гипотеза

58) Чем больше значение р-уровня, тем…

59) Вероятность того, что в генеральной совокупности нулевая гипотеза верна, есть показатель…

60) Результат проверки гипотезы признается статистически достоверным, если…

61) Может ли одно и то же численное значение корреляции для разных выборок иметь разную статистическую значимость?

62) Для 1-ой выборки корреляция Rxy =0,30 (p =0,05), для 2-ой выборки Rxy =0,60 (p =0,05). Почему p-уровень одинаковый?

63) Для 1-ой выборки корреляция Rxy =0,35 (p =0,06), для 2-ой выборки Rxy =0,35 (p =0,03). Почему p-уровень разный?

64) Могут ли разные значения корреляции (например, 0,4 и 0,6) иметь одинаковую статистическую значимость?

65) При сравнении двух средних (М1=5, М2=7) значение р -уровня будет тем меньше, чем

66) При сравнении двух распределений частот с использованием критерия Хи-квадрат значение р -уровня больше, если

67) Гомогенность (равенство) дисперсий проверяется перед:

68) При сравнении средних для независимых выборок одним из обязательных условий является проверка:

69) Если при сравнении средних для 2-х независимых выборок неравной численности дисперсии статистически значимо различаются, то следует:

70) Если при сравнении средних для нескольких независимых выборок неравной численности дисперсии статистически достоверно различаются, то следует:

71) Если при сравнении 2-х средних для независимых выборок неравной численности оказалось, что дисперсии различаются статистически достоверно, то следует

72) Если при проверке статистической достоверности корреляции (при α = 0,05) р> 0.1, то корректен вывод, что

73) Если при проверке статистической достоверности корреляции (при α = 0,05) р< 0.05, то корректен вывод, что

74) Если при проверке статистической значимости различий двух средних р> 0.1, то делают вывод о том, что

75) Если при проверке статистической значимости различий двух средних (при α = 0,05) р> 0.05, то делают вывод о том, что

76) Для проверки достоверности различия двух независимых групп, члены которых ранжированы по степени выраженности «тревожности», применяют критерий

77) Для проверки достоверности различия двух повторных измерений, члены которых ранжированы по степени выраженности «тревожности», применяют критерий

78) Для проверки достоверности различий студентов 1 и 5 курсов по переменной «семейное положение» (холост – нет) следует применить критерий

79) Для проверки достоверности различий 2-х выборок по переменной «пол» (муж - жен) следует применить критерий

80) Для сравнения преподавателей и студентов по «доминантности» (метрическая шкала), следует применить критерий

81) Для сравнения двух независимых выборок по количественной переменной, имеющей заметные выбросы, применяют критерий

82) Для проверки различия самочувствия (метрическая шкала) до и после терапии применяют критерий

83) Если необходимо сравнить два повторных измерения количественной переменной, имеющей заметные выбросы, то применяют критерий

84) Для проверки достоверности различия двух зависимых выборок по переменной, измеренной в ранговой шкале, применяют критерий

85) Для проверки достоверности различия старших (1-я выборка) и их младших (2-я выборка) братьев по уровню доминантности, измеренной в метрической шкале, применяют критерий

86) Гипотезу о взаимосвязи номинативной (2 градации) и ранговой переменных целесообразно проверять при помощи

87) Гипотезу о взаимосвязи номинативной (2 градации) и метрической переменных целесообразно проверять при помощи

88) Статистическая значимость улучшения состояния (ранговая шкала) до и после терапии определяется по критерию

89) Гипотезу о взаимосвязи ранговой и номинативной переменной, имеющей две градации (напр., пол), целесообразно изучать при помощи критерия

90) Для проверки достоверности различия 2 групп, каждый член которых определен в одну из трех категорий («правый», «левый», «центрист»), применяют критерий

91) Для проверки гипотезы о различии 2 групп по степени индивидуальной изменчивости (дисперсии) применяют критерий

92) Гипотезу о взаимосвязи метрической и номинативной переменной, имеющей 5 градаций (например, хобби), целесообразно проверять при помощи

93) Гипотезу о взаимосвязи порядковой и номинативной переменной, имеющей 4 градации (напр., должность), целесообразно изучать при помощи критерия

94) Гипотезу о взаимосвязи метрической и порядковой переменной, имеющей 15 градаций, целесообразно изучать при помощи

95) Гипотезу о взаимосвязи 2-х количественных переменных, имеющих заметные выбросы (асимметрии) целесообразно проверять при помощи

96) Для проверки гипотезы о взаимосвязи одной метрической переменной и двух номинативных переменных целесообразно применять:

97) Для проверки гипотезы о взаимосвязи одной метрической переменной и одной номинативной переменных с 3 и более значениями целесообразно применять:

98) Для проверки гипотезы о взаимосвязи одной метрической переменной и трех номинативных переменных целесообразно применять:

99) Но об идентичности зависимых выборок по уровню выраженности переменной, измеренной в ранговой шкале (при α = 0,05) отклоняется, если:

100) Но об идентичности зависимых выборок по уровню выраженности переменной, измеренного в метрической шкале (при α = 0,05) отклоняется, если:

101) Но об идентичности независимых выборок по уровню выраженности переменной, измеренной в метрической шкале (при α = 0,05) отклоняется, если:

102) Но об отсутствии взаимосвязи двух номинальных переменных (при α = 0,05) отклоняется, если:

103) Но об отсутствии взаимосвязи двух номинальных переменных (при α = 0,05) не отклоняется, если:

104) Но об отсутствии взаимосвязи двух порядковых переменных (при α = 0,05) не отклоняется, если:

105) Но об отсутствии взаимосвязи двух порядковых переменных (при α = 0,05) отклоняется, если:

106) Статистическая гипотеза Но о равенстве двух средних значений (N1=60; N2=70) не отклоняется (при α = 0,01), если:

107) Но об отсутствии различий двух распределений номинативного признака отклоняется (при α = 0,05), если:

108) Но об отсутствии различий дисперсий двух независимых выборок (при α = 0,05) отклоняется, если:

109) Но об отсутствии различий дисперсий двух независимых выборок (при α = 0,05) не отклоняется, если:

110) Статистическая гипотеза Но о равенстве двух средних значений (N1=60; N2=70) отклоняется (при α = 0,01), если:

111) Статистическая гипотеза Но о корреляции двух переменных

(N = 18) отклоняется (при α = 0,01), если:

112) Статистическая гипотеза Но о корреляции двух переменных

(N = 18) не отклоняется (при α = 0,01), если:

113) Если при сравнении 2-х средних при помощи компьютера получен следующий результат: t=2,48; p=0,045, то различие между соответствующими группами по измеренному признаку (при α = 0,05)

114) Если при сравнении 2-х средних значений (при α = 0,01) получен следующий результат: t=2,56; p=0,12, то различие групп по измеренному признаку

115) Если при вычислении корреляции получен результат: r34=0,36; p=0,14, то взаимосвязь между признаками 3 и 4 (при α = 0,05):

116) Взаимодействие факторов в дисперсионном анализе обозначает, что влияние одного из этих факторов на зависимую переменную…

117) Взаимодействие факторов «Пол» и «Группа» в ANOVA обозначает, что различия между группами

118) Отсутствие взаимодействия факторов в дисперсионном анализе обозначает, что влияние одного из этих факторов на зависимую переменную…

119) ANOVA предполагает предварительную проверку

120) Средний квадрат (MS) в ANOVA это

121) В ANOVA межгрупповая SS это

122) В ANOVA внутригрупповая SS это

123) В ANOVA внутригрупповая (случайная) сумма квадратов вычисляется как:

124) Стандартная таблица результатов ANOVA содержит следующую последовательность столбцов

125) ANOVA предполагает следующую последовательность вычисления показателей:

126) Коэффициент детерминации (R2, RSQ) в дисперсионном анализе это отношение

127) Для проверки равенства (гомогенности) дисперсий в ANOVA применяется критерий

128) Перед проведением ANOVA с неравной численностью выборок необходимо

129) Для множественного сравнения средних в рамках дисперсионного анализа не применяют

130) Для множественного сравнения средних в рамках дисперсионного анализа применяют

131) Метод множественного сравнения средних который требует (не требует) предварительного получения статистически значимого результата дисперсионного анализа это

132) Метод Post Hoc – это метод

133) Метод контрастов – это метод

134) В ANOVA F-отношение – это частное от деления:

135) При помощи 4-факторного ANOVA проверяется:

136) Сколько гипотез о взаимодействии проверяется при помощи 4-факторного ANOVA:

137) Ковариата в дисперсионном анализе это

138) Многомерный дисперсионный анализ предназначен для изучения влияния

139) Дисперсионный анализ с повторными измерениями позволяет изучать влияние на зависимые переменные

140) Внутригрупповым (ВГ) и межгрупповым (МГ) факторам в дисперсионном анализе с повторными измерениями соответствуют выборки:

141) Сходство этих двух многомерных методов заключается в том, что анализируются различия (сходства) между объектами:

142) Сходство этих двух многомерных методов заключается в их назначении – классификации объектов:

143) Сходство этих двух многомерных методов заключается в их назначении – предсказании значений зависимой переменой:

144) Сходство этих двух многомерных методов заключается в их назначении – анализе структуры с целью выделения латентных переменных:

145) Различие этих двух многомерных методов заключается в том, в какой шкале представлена зависимая переменная (в первом – метрическая, во втором – номинативная):

146) Различие этих двух методов классификации заключается в том, что в первом задано число классов и принадлежность некоторых объектов к этим классам, а во втором – не задано ни то ни другое:

147) Сходство этих двух многомерных методов заключается в том, что анализируются корреляции между признаками:

148) Часть дисперсии «зависимой» переменной, обусловленная влиянием «независимых» переменных в МРА – это…

149) Если независимая переменная х в множественном регрессионном анализе коррелирует с другими независимыми переменными, то ее вклад в дисперсию зависимой переменной…

150) Если независимая переменная х в множественном регрессионном анализе не коррелирует с другими независимыми переменными, то ее вклад в оценку зависимой переменной…

151) Критерий Кайзера λ > 1 применяют для…

152) Для предварительной оценки числа факторов в факторном анализе используют…

153) Величина факторной нагрузки данной переменной по данному фактору свидетельствует …

154) Квадрат факторной нагрузки переменной по данному фактору есть величина…

155) Общность в факторном анализе это доля дисперсии…

156) Какая из перечисленных проблем решается исследователем в процессе проведения факторного анализа

157) Какая из перечисленных проблем не решается в процессе проведения факторного анализа?

158) Слева внизу перечислены проблемы факторного анализа. Выберите справа вариант, соответствующий правильной последовательности решения этих проблем.

159) Слева внизу перечислены шаги факторного анализа. Выберите справа вариант, соответствующий правильной их последовательности.

 

  Факторы (160) Факторы следует интерпретировать:  
(161) Общность переменной № 5 равна:   (162) Какой фактор более мощный (по доли дисперсии):  

(163) Чему равен восстановленный коэффициент корреляции r12

 
  F1 F2
  0,7 0,1
  0,8 0,4
  0,1 0,7
  0,2 -0,7
  -0,7 0,4
 

 
3.1.5 Методические материалы для оценки обучающимися содержания и качества учебного процесса
Анкеты, опросные листы для оценки обучающимися содержания и качества учебного процесса по данной дисциплине утверждаются Ученым Советом факультета.
3.2. Кадровое обеспечение
3.2.1 Образование и (или) квалификация преподавателей и иных лиц, допущенных к проведению учебных занятий
К чтению лекций должны привлекаться преподаватели, имеющие ученую степень по психологии, ведущие специалисты в области методологии применения математических методов в психологии. К проведению семинарских занятий могут привлекаться преподаватели, имеющие базовое психологическое образование, соответствующее профилю преподаваемой дисциплины
3.2.2 Обеспечение учебно-вспомогательным и (или) иным персоналом
Не требуется
3.3. Материально-техническое обеспечение
3.3.1 Характеристики аудиторий (помещений, мест) для проведения занятий
Для лекций и практических занятий: стандартно оборудованные лекционные аудитории и компьютерные классы, отвечающие санитарным нормам, предусмотренным Образовательным стандартом реализации программ высшего профессионального образования Санкт-Петербургского государственного университета, предусматривающие проведение лекций и занятий с мультимедиа.
3.3.2 Характеристики аудиторного оборудования, в том числе неспециализированного компьютерного оборудования и программного обеспечения общего пользования
Минимально необходимый перечень материально-технического обеспечения лекционных занятий включает: лекционные аудитории с компьютерным и видеопроекционным оборудованием для презентаций с выходом в Интернет, средствами звуковоспроизведения и экраном. Минимально необходимый перечень материально-технического обеспечения практических занятий включает: компьютерные классы оборудованные компьютерами в количестве по 1 компьютеру на каждого учащегося и 1 компьютер для преподавателя, дополненный видеопроекционным оборудованием и экраном.
3.3.3 Характеристики специализированного оборудования
Не требуется
3.3.4 Характеристики специализированного программного обеспечения
Наличие установленных на каждый компьютер в компьютерном классе программ IBM SPSS Statistics и AMOS последних версий.
3.3.5 Перечень и объем расходных материалов
Доски, мел, губки, маркеры, фломастеры, бумага формата А4, канцелярские товары, картриджи принтеров, диски, флеш-накопители и др. в объёме, необходимом для организации и проведения занятий (по заявкам преподавателей, подаваемым в установленные сроки).
3.4. Информационное обеспечение
3.4.1 Список обязательной литературы
1. Наследов А.Д. Математические методы психологического исследования: анализ и интерпретация данных. СПб, 2011. 2. Наследов А.Д. SPSS19: профессиональный статистический анализ данных. СПб, 2011. 3. Наследов А.Д. IBM SPSS Statistics 20 и AMOS: профессиональный статистический анализ данных. – СПб., 2013.
3.4.2 Список дополнительной литературы
1. Byrne, B. M. (2010). Structural Equation Modeling With AMOS: Basic Concepts, Applications,and Programming (2nd ed.) (Multivariate applications series). New York: Taylor & Francis Group. 396 p. 2. Harrington, D. (2009). Confirmatory factor analysis. New York: Oxford University Press, Inc. 122 p. 3. Kline, R. B. (2011). Principles and practice of structural equation modeling (3nd ed.). New York: The Guilford Press. 432 p. 4. Берка К. Измерения: понятия, теории, проблемы. М., 1987. 5. Гусев А.Н. Дисперсионный анализ в экспериментальной психологии. М., 2000. 6. Дэйвисон М. Многомерное шкалирование: методы наглядного представления данных. М., 1988. 7. Закс Л. Статистическое оценивание. М., 1976. 8. Крамер Д. Математическая обработка данных в социальных науках: современные методы: учеб. пособие для студ. высших учеб. заведений. М., 2007. 9. Митина О.В. Моделирование латентных изменений с помощью структурных уравнений // Экспериментальная психология. 2008. №1. С. 131-148. 10. Митина О.В. Основные идеи и принципы структурного моделирования // Ученые записки кафедры общей психологии МГУ. Вып.2: Смысл, 2006. С. 272-296. 11. Митина О.В., Михайловская И.Б. Факторный анализ для психологов. М., 2001. 12.., 1976.И. Теория измерений. еской психологиионным оборудованием и экраном. Суходольский Г.В. Основы математической статистики для психологов. Л., 1972.
3.4.3 Перечень иных информационных источников
Журналы: § Журнал «Вестник Санкт-Петербургского университета», серия 12 Психология, Социология. Педагогика. § Журнал «Вопросы психологии»; § «Психологический журнал» РАН; Интернет-ресурсы: Информационные ресурсы Санкт-Петербургского государственного университета: URL: https://www.lib.pu.ru Информационные ресурсы Московского психолого-педагогического университета: URL: https://www.childpsy.ru Научный электронный журнал «Журнал практической психологии и психоанализа». https://www.psyjournal.ru/ Научный электронный журнал «Психологические исследования». URL: https://psystudy.ru/ https://voppsy.ru (журнал «Вопросы психологии»), https://psychol.ras.ru/08.shtml («Психологический журнал»), https://www.psy.msu.ru/science/vestnik/index.html(«Вестник Московского университета» Серия 14.Психология) Cambridge University Press (CUP) URL: https://www.journals.cambridge.org/ EBSCO URL:https://search.ebscohost.com, Academic Search Premier Научная электронная библиотека eLIBRARY.RU URL:https://elibrary.ru/ Elsevier (платформа Science Direct) URL:https://www.jstor.org Oxford University Press URL:https://www3.oup.co.uk/jnls/ Springer/Kluwer URL:https://www.springerlink.com Web of Science URL:https://isiknowledge.com Университетская информационная система Россия URL: https://www.cir.ru/index.jsp  
Раздел 4. Разработчики программы
Фамилия, имя, отчество Учёная Учёное Должность Контактная информация
степень звание (служебный адрес электронной почты, служебный телефон)
Наследов Андрей Дмитриевич к. пс. н Доц. доцент кафедры Педагогики и педагогической психологии a.nasledov@spbu.ru 328-94-08

 



Поделиться:




Поиск по сайту

©2015-2024 poisk-ru.ru
Все права принадлежать их авторам. Данный сайт не претендует на авторства, а предоставляет бесплатное использование.
Дата создания страницы: 2020-01-14 Нарушение авторских прав и Нарушение персональных данных


Поиск по сайту:

Читайте также:

Деталирование сборочного чертежа

Когда производственнику особенно важно наличие гибких производственных мощностей?

Собственные движения и пространственные скорости звезд

Тема 11. Банковские риски и способы их оценки

Опросник «Активность повседневной жизни»

Интересно:

Как устроена магнитная головка

Что такое технологическая операция и каковы виды технологических операций?

Что такое нейролингвистика?

Что такое ХЭШТЕГ и как им пользоваться в сети

Обратная связь