Практическая часть
Главной задачей при решении тригонометрических уравнений является приведение уравнение к такому виду, чтобы слева у вас была элементарная тригонометрическая функция, а справа число. Всё, что остаётся сделать, - это найти значение аргумента функции (х) используя формулу выражения аргумента через обратные тригонометрические функции.
Чаще всего для этого, надо попытаться:
1. привести все функции входящие в уравнение к «од инаковым углам»;
2. привести уравнение к «одинаковым функциям»;
3. разложить левую часть уравнения на множители и т.п.
Метод замены переменной
Рассмотрим примеры решения тригонометрических уравнений, которые после введения нового неизвестного t = f(x), где f(x) – одна из основных тригонометрических функций, превращаются в квадратные или рациональные уравнения с неизвестным t.
Схема решения:
Шаг 1. Привести уравнение к алгебраическому виду относительно одной из тригонометрических функций.
Шаг 2. Обозначить полученную функцию переменной t (если необходимо, ввести ограничения на t).
Шаг 3. Записать и решить полученное алгебраическое уравнение.
Шаг 4. Сделать обратную замену.
Шаг 5. Решить простейшее тригонометрическое уравнение.
Пример 1
1) 
Введём новое неизвестное cosx = t, тогда уравнение (1) превратится в квадратное уравнение с неизвестным t: их исходного уравнения это уравнение
2)  не получается
не получается
Решив уравнение (2), мы получим два корня  и
и  .
.
Не стоит забывать об области определения тригонометрических функций, косинус не может принять значение -2, следовательно, мы продолжим работу с корнем 
Множество решений уравнения (1) есть множество решения уравнения
 Решая это простейшее тригонометрическое уравнение, находим, что множество всех решений уравнения (1) состоит из двух серий решений:
Решая это простейшее тригонометрическое уравнение, находим, что множество всех решений уравнения (1) состоит из двух серий решений:
 ;
; 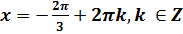 .
.
Пример 2
3)  .
.
Заменим sin x на t и получим распадающееся уравнение:
 Имеющее два решения
Имеющее два решения  и
и  .
.
Множество всех решений уравнения (3) есть объединение множество всех решений двух уравнений:
 = 0,5 и sin x = -1
= 0,5 и sin x = -1
Решая эти простейшие тригонометрическое уравнение, находим, что множество всех решений уравнения (3) состоит из трех серий решений:
 ;
;  ;
; 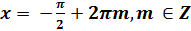 .
.
Метод разложения на множители
Если уравнение f (х) = 0 удается преобразовать к виду  , то решение данного уравнения сводится к решению уравнений
, то решение данного уравнения сводится к решению уравнений 
Многие тригонометрические уравнения, правая часть которых равна нулю, решаются с помощью разложения левой части на множители.
Пример 1
1) 
Используя формулу для синуса двойного аргумента, запишем уравнение в виде :

Вынося общий множитель sinx за скобки, получаем:
2) 
Уравнение 2 распадается на два уравнения:
 и
и 
Решая эти простейшие тригонометрическое уравнение, находим, что множество всех решений уравнения 1 состоит из трех серий решений:
 ;
;  ;
; 
Применение основных тригонометрических формул для решения уравнений
В этом пункте на примерах показано применение некоторых тригонометрических формул при решении уравнений.
1.Применение основного тригонометрического тождества.
Решим уравнение:
1)  =2
=2 
Применяя основное тригонометрическое тождество  ,
,  :
:
2) 
Введем новое неизвестное sin x = t, получим квадратное уравнение с неизвестным t:
3) 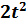 + 3t – 2 = 0
+ 3t – 2 = 0
Уравнение 3 имеет два корня  и
и  .
.
Множество решений уравнения 2, а значит и уравнения 1 есть множество решений уравнений:
 -2 и sin x =
-2 и sin x =  .
.
Первое уравнение не имеет решений, следовательно все решения уравнения 1 состоят из множества решений второго уравнения, которое имеет две серии решений:
 ;
;  .
.
2. Применение формул сложения
Решим уравнение:

Перенеся все члены уравнения в левую часть, и применив формулу синуса разности двух углов 
 получим:
получим:

Решения уравнения 2 и уравнения 1 удовлетворяют условию:
 , откуда следует одна серия решений:
, откуда следует одна серия решений:
 .
.
3. Понижение кратности углов
Иногда при решении тригонометрических уравнений бывает удобно синусы и косинусы кратных углов выражать через синусы и косинусы самих этих углов.
Решим уравнение:
 x = 1
x = 1
Используя формулу синуса двойного угла, перепишем уравнение в виде:
 Применив основное тригонометрическое тождество, перепишем это уравнение в виде:
Применив основное тригонометрическое тождество, перепишем это уравнение в виде:
 Уравнение 2, а значит и уравнение 1 имеет две серии решений:
Уравнение 2, а значит и уравнение 1 имеет две серии решений:
 ;
;  .
.
Понижение степени уравнения
Если в уравнении есть синус или косинус в четной степени, то, используя для этого формулы понижения степени и выражая квадраты синуса и квадраты косинуса половинного угла, можно понизить степень уравнения.
sin2 x = 1/2(1 – cos 2x);
cos2 x = 1/2 · (1 + cos 2x);
tg2 x = (1 – cos 2x) / (1 + cos 2x).
Решим уравнение:
 Используя формулу для квадрата косинуса из списка выше, перепишем уравнение:
Используя формулу для квадрата косинуса из списка выше, перепишем уравнение:
 Приведя к общему знаменателю и сложив подобные члены получим:
Приведя к общему знаменателю и сложив подобные члены получим:
3) 
Уравнение имеет две серии корней:
 ;
; 
5. Введение вспомогательного угла
Решим уравнение:
1) 
Поделив уравнение на 2, получим:
2) 
Замечаем:  ;
; 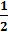 = sin
= sin  ,
,  - это и есть наш дополнительный угол, перепишем уравнение 2:
- это и есть наш дополнительный угол, перепишем уравнение 2:

Используя формулу косинуса суммы, получим:
 Уравнение имеет две серии корней
Уравнение имеет две серии корней
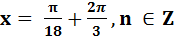 ;
; 
6. Преобразование произведения в сумму
Известно, что любая математическая формула на практике применяется как справа налево, так и слева направо. В тригонометрии мы можем преобразовать сумму тригонометрических функций в произведение и наоборот, используя формулы:
 ;
;
cos a  ;
;
sin a 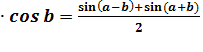
Решим уравнение:

Используя формулу произведения синусов, перепишем его как:
2) cos8x=0
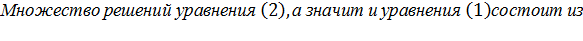


7. Универсальная тригонометрическая подстановка
Универсальная тригонометрическая подстановка – это формулы для выражения синуса, косинуса и тангенса аргумента через тангенс половинного аргумента:
 ;
;  ;
; 
Решим уравнение:
1) 
Применив формулы для универсальной тригонометрической подстановки, получим:
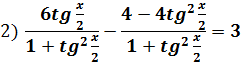 Приведя подобные члены и сделав замену
Приведя подобные члены и сделав замену  , перепишем уравнение:
, перепишем уравнение:
3) 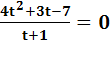
Решая уравнение 3, учитывая, что t  -1, получим корни:
-1, получим корни:
 Множество решений уравнения 3, а значит и уравнения 1 есть множество решений уравнений:
Множество решений уравнения 3, а значит и уравнения 1 есть множество решений уравнений:
 ;
; 
Решив эти уравнения, получим:
 ;
;  .
.
Однородные уравнения
Уравнение  , где a
, где a  и b
и b  , называют однородным тригонометрическим уравнением первой степени.
, называют однородным тригонометрическим уравнением первой степени.
Отличительные признаки однородных уравнений:
а) все одночлены имеют одинаковую степень;
б) свободный член равен нулю;
в) в уравнении присутствуют степени с двумя различными основаниями.
Пример 1.
Решим уравнение:

Чтобы решить уравнение такого типа, разделим обе части уравнения на
cos x  и получим:
и получим:
2) 
Множество решений уравнения 2, а значит и уравнения 1 состоит из одной серии корней:
 . период посмотри в формуле
. период посмотри в формуле
Пример 2.
Решим уравнение:
1) 
Вынесем  за скобки:
за скобки:
2) сos x 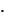 (
( 
Уравнение 2 распадается на два уравнения:
 и 4)
и 4) 
Решение уравнения 3:

Уравнение 4 - однородное тригонометрическое уравнение первой степени. Чтобы его решить, разделим обе части уравнения на  .
.
Получим: 5) 
Решение уравнения 5:
 .
.
Множество всех решений уравнения 1 есть объединение множество решений уравнений 3 и 5.