Пружинный маятник.
Пружинный маятник — механическая система, состоящая из пружины с коэффициентом упругости (жёсткостью) k (закон Гука), один конец которой жёстко закреплён, а на втором находится груз массы m.
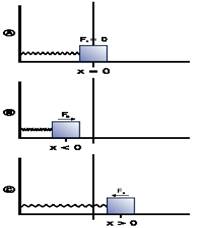
Когда на массивное тело действует упругая сила, возвращающая его в положение равновесия, оно совершает колебания около этого положения.Такое тело называют пружинным маятником. Колебания возникают под действием внешней силы. Колебания, которые продолжаются после того, как внешняя сила перестала действовать, называют свободными. Колебания, обусловленные действием внешней силы, называют вынужденными. При этом сама сила называется вынуждающей.
В простейшем случае пружинный маятник представляет собой движущееся по горизонтальной плоскости твердое тело, прикрепленное пружиной к стене.
Второй закон Ньютона для такой системы при условии отсутствия внешних сил и сил трения имеет вид:
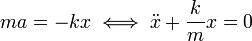
Если на систему оказывают влияние внешние силы, то уравнение колебаний перепишется так:
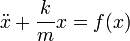— это равнодействующая внешних сил соотнесённая к единице массы груза.
В случае наличия затухания, пропорционального скорости колебаний с коэффициентом c:
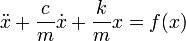
Резонанс.
Резона́нс (фр. resonance, от лат. resono — откликаюсь) — явление резкого возрастания амплитуды вынужденных колебаний, которое наступает при приближении частоты внешнего воздействия к некоторым значениям (резонансным частотам), определяемым свойствами системы. Увеличение амплитуды — это лишь следствие резонанса, а причина — совпадение внешней (возбуждающей) частоты с внутренней (собственной) частотой колебательной системы. При помощи явления резонанса можно выделить и/или усилить даже весьма слабые периодические колебания. Резонанс — явление, заключающееся в том, что при некоторой частоте вынуждающей силы колебательная система оказывается особенно отзывчивой на действие этой силы. Степень отзывчивости в теории колебаний описывается величиной, называемой добротность. Явление резонанса впервые было описано Галилео Галилеем в 1602 г в работах, посвященных исследованию маятников и музыкальных струн.
|
|
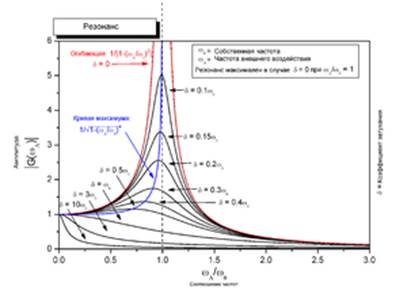
Явление резонанса.
Явление резонанса относится к наиболее важным с практической точки зрения свойствам электрических цепей. Оно заключается в том, что электрическая цепь, имеющая реактивные элементы обладает чисто резистивным сопротивлением.
Общее условие резонанса для любого двухполюсника можно сформулировать в виде Im[Z]=0 или Im[Y]=0, где Z и Y комплексное сопротивление и проводимость двухполюсника. Следовательно, режим резонанса полностью определяется параметрами электрической цепи и не зависит от внешнего воздействия на нее со стороны источников электрической энергии.
Для определения условий возникновения режима резонанса в электрической цепи нужно:
найти ее комплексное сопротивление или проводимость;
выделить мнимую часть и приравнять нулю.
Все параметры электрической цепи, входящие в полученное уравнение, будут в той или иной степени влиять на характеристики явления резонанса.
Уравнение Im[Z]=0 может иметь несколько корней решения относительно какого-либо параметра. Это означает возможность возникновения резонанса при всех значениях этого параметра, соответствующих корням решения и имеющих физический смысл.
|
|
В электрических цепях резонанс может рассматриваться в задачах:
анализа этого явления при вариации параметров цепи;
синтеза цепи с заданными резонансными параметрами.
Электрические цепи с большим количеством реактивных элементов и связей могут представлять значительную сложность при анализе и почти никогда не используются для синтеза цепей с заданными свойствами, т.к. для них не всегда возможно получить однозначное решение. Поэтому на практике исследуются простейшие двухполюсники и с их помощью создаются сложные цепи с требуемыми параметрами.
Простейшими электрическими цепями, в которых может возникать резонанс, являются последовательное и параллельное соединения резистора, индуктивности и емкости. Соответственно схеме соединения, эти цепи называются последовательным и параллельным резонансным контуром. Наличие резистивного сопротивления в резонансном контуре по определению не является обязательным и оно может отсутствовать как отдельный элемент (резистор). Однако при анализе резистивным сопротивлением следует учитывать по крайней мере сопротивления проводников.
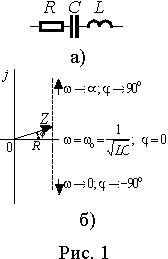
Последовательный резонансный контур представлен на рис. 1 а). Комплексное сопротивление цепи равно
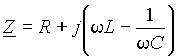
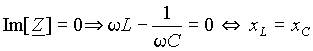
Таким образом, резонанс в цепи наступает независимо от значения резистивного сопротивления R когда индуктивное сопротивление xL = w L равно емкостному xC = 1/(w C). Как следует из выражения (2), это состояние может быть получено вариацией любого их трех параметров - L, C и w, а также любой их комбинацией. При вариации одного из параметров условие резонанса можно представить в виде
|
|
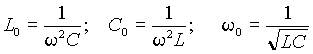
Все величины, входящие в выражение (3) положительны, поэтому эти условия выполнимы всегда, т.е. резонанс в последовательном контуре можно создать
изменением индуктивности L при постоянных значениях C и w;
изменением емкости C при постоянных значениях L и w;
изменением частоты w при постоянных значениях L и C.
Наибольший интерес для практики представляет вариация частоты. Поэтому рассмотрим процессы в контуре при этом условии.
При изменении частоты резистивная составляющая комплексного сопротивления цепи Z остается постоянной, а реактивная изменяется. Поэтому конец вектора Z на комплексной плоскости перемещается по прямой параллельной мнимой оси и проходящей через точку R вещественной оси (рис. 1 б)). В режиме резонанса мнимая составляющая Z равна нулю и Z = Z = Zmin = R, j = 0, т.е. полное сопротивление при резонансе соответствует минимальному значению
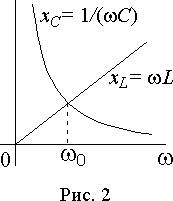Индуктивное и емкостное сопротивления изменяются в зависимости от частоты так, как показано на рис. 2. При частоте стремящейся к нулю xC ® µ, xL ® 0, и j ® - 90° (рис. 1 б)). При бесконечном увеличении частоты - xL ® µ, xC ® 0, а j ® 90°. Равенство сопротивлений xL и xC наступает в режиме резонанса при частоте w0.
Рассмотрим теперь падения напряжения на элементах контура. Пусть резонансный контур питается от источника, обладающего свойствами источника ЭДС, т.е. напряжение на входе контура u = const, и пусть ток в контуре равен i=Imsinw t. Падение напряжения на входе уравновешивается суммой напряжений на элементах
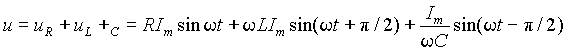
Переходя от амплитудных значений к действующим, из выражения (4) получим напряжения на отдельных элементах контура
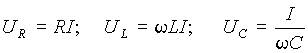
а при резонансной частоте
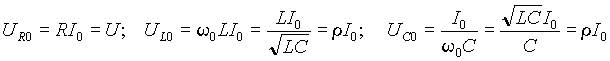
Звук. Виды звука, и их применения.
Звук, в широком смысле — упругие волны, распространяющиеся в какой-либо упругой среде и создающие в ней механические колебания; в узком смысле — субъективное восприятие этих колебаний специальными органами чувств животных или человека.
Как и любая волна, звук характеризуется амплитудой и спектром частот. Обычно человек слышит звуки, передаваемые по воздуху, в диапазоне частот от 16—20 Гц до 15—20 кГц[1]. Звук ниже диапазона слышимости человека называют инфразвуком; выше: до 1 ГГц, — ультразвуком, от 1 ГГц — гиперзвуком. Среди слышимых звуков следует также особо выделить фонетические, речевые звуки и фонемы (из которых состоит устная речь) и музыкальные звуки (из которых состоит музыка).
Различают продольные и поперечные звуковые волны в зависимости от соотношения направления распространения волны и направления механических колебаний частиц среды распространения.
Виды звуков.
Мы воспринимаем большое количество различных звуков. Но не все звуки одинаково используются в музыке. Все существующие в природе звуки делятся на музыкальные и шумовые. Основную роль в музыке играют музыкальные звуки, хотя используются и шумовые (в частности почти все ударные инструменты издают шумовые звуки).
Шумовые звуки не имеют точно выраженной высоты, например треск, скрип, стук, гром, шорох и т. п. Шумовые инструменты применяются лишь в качестве украшения или придания музыке эмоциональной насыщенности. К таким инструментам относятся почти все ударные: треугольник, малый барабан, разнообразные виды тарелок, большой барабан и др. В этом присутствует некоторая доля условности, о которой не следует забывать. Например, такой ударный инструмент как "деревянная коробочка" имеет звучание с достаточно ясно выраженной высотностью, однако этот инструмент все равно причисляется к шумовым. Поэтому отличать шумовые инструменты надежнее по тому критерию, возможно ли на данном инструменте исполнить мелодию, или нет.
Музыкальными называются звуки, имеющие определённую высоту, которую можно измерить с абсолютной точностью. Всякий музыкальный звук можно повторить голосом или на каком-либо инструменте.