#Нелинейным является уравнение регрессии нелинейное относительно входящих в него …
+факторов
-результатов
-параметров
-случайных величин
#Если спецификация модели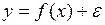 
нелинейное уравнение регрессии, то нелинейной является функция…
+ 
- 
- 
- 
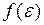
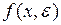
#Нелинейным не является уравнение …
+ 
- 
- 
- 
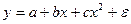
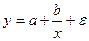
#Нелинейным является уравнение …
+
-
- 
- 
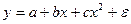
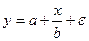
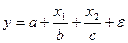
#Нелинейное уравнение регрессии означает нелинейную форму зависимости между …
+результатом и факторами
-фактором и результатами
-результатом и параметрами
-фактором и случайной величиной
#Если спецификация модели отображает нелинейную форму зависимости между экономическими показателями, то нелинейно уравнение …
+регрессии
-корреляции
-детерминации
-аппроксимации
#Уравнение регрессии 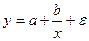характеризует ______ зависимость
+обратно пропорциональную
-линейную
-прямо пропорциональную
-функциональную
#Спецификация модели нелинейная парная регрессия подразумевает нелинейную зависимость и …
+независимую переменную
-пару независимых переменных
-пару зависимых переменных
-пару существенных переменных
#Нелинейным называется уравнение регрессии, если …
+независимые переменные входят в уравнение нелинейным образом
-параметры входят нелинейным образом, а переменные линейны
-зависимые переменные входят в уравнение нелинейным образом
-параметры и зависимые переменные входят в уравнение нелинейным образом
#В нелинейной модели парной регрессии 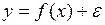функция является …
+нелинейной
-линейной
-равной нулю
-несущественной
#Экспоненциальным не является уравнение регрессии …
+ 
- 
- 
- 
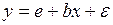
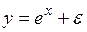
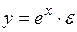
#Примером нелинейной зависимости экономических показателей является …
|
|
+классическая гиперболическая зависимость спроса от цены
-линейная зависимость выручки от величины оборотных средств
-зависимость объема продаж от недели реализации
-линейная зависимость затрат на производство от объема выпуска продукции
#При выборе спецификации нелинейная регрессия используется, если …
+между экономическими показателями обнаруживается нелинейная зависимость
-между экономическими показателями не обнаруживается нелинейная зависимость
-нелинейная зависимость для исследуемых экономических показателей является несущественной
-между экономическими показателями обнаруживается линейная зависимость
#Было замечено, что при увеличении количества вносимых удобрений урожайность также возрастает, однако, по достижении определенного значения фактора моделируемый показатель начинает убывать. Для исследования данной зависимости можно использовать спецификацию уравнения регрессии …
+ 
- 
- 
- 
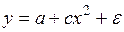
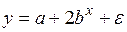
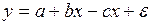
#Известно, что с увеличением объема производства себестоимость единицы продукции уменьшается за счет того, что происходит перераспределение постоянных издержек. Пусть а – совокупная величина постоянных издержек, а b – величина переменных издержек в расчете на 1 изделие. Тогда зависимость себестоимости единицы продукции от объема производства можно описать с помощью модели …
+ 
- 
- 
- 
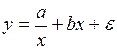
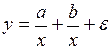
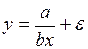
#Если между экономическими показателями существует нелинейная связь, то …
+целесообразно использовать спецификацию нелинейного уравнения регрессии
|
|
-необходимо включить в модель другие факторы и использовать линейное уравнение множественной регрессии
-нецелесообразно использовать спецификацию нелинейного уравнения регрессии
-целесообразно использовать линейное уравнение парной регрессии
#Парабола второй степени может быть использована для зависимостей экономических показателей, если
+если для определенного интервала значений фактора меняется характер связи рассматриваемых показателей: прямая связь изменяется на обратную или обратная на прямую
-если исходные данные не обнаруживают изменения направленности
-если для определенного интервала значений фактора меняется скорость изменений значений результата, то есть возрастает динамика роста или спада
-если характер связи зависит от случайных факторов
#Для моделирования зависимости предложения от цены не может быть использовано уравнение регрессии …
+ 
- 
- 
- 
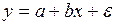
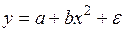
#Нелинейную модель зависимостей экономических показателей нельзя привести к линейному виду, если …
+нелинейная модель является внутренне нелинейной
-нелинейная модель является внутренне линейной
-линейная модель является внутренне нелинейной
-линейную модель является внутренне линейной
#Проводится исследование финансовых результатов деятельности предприятий, среди которых обнаруживаются как прибыльные, так и убыточные. Среди ряда факторов, влияющих на прибыль, был выделен доминирующий. При этом нельзя использовать спецификацию …
+ 
- 
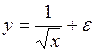
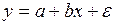, (a < 0)
-
- 
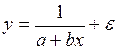
#По результатам исследования было выявлено, что рентабельность производства падает с увеличением трудоемкости. Какую спецификацию уравнения регрессии можно использовать для построения модели такой зависимости?
|
|
+ 
- 
-
- 
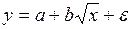
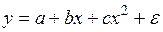
#При помощи модели степенного уравнения регрессии вида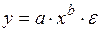 
(b >0) не может быть описана зависимость …
+выработки ль трудоемкости
-заработной платы от выработки
-выработки от уровня квалификации
-объема предложения от цены
#К линейному уравнению нельзя привести …
+ 
- 
- 
- 
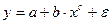
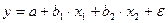
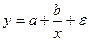
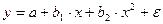
#Линеаризация подразумевает процедуру …
+приведения нелинейного уравнения к линейному виду
-приведения линейного уравнения к нелинейному виду
-приведения нелинейного уравнения относительно параметров к уравнению, линейному относительно результата
-приведения уравнения множественной регрессии к парной
#Уравнение … может быть линеаризовано при помощи подстановки …
+ 
- 
- 
- 
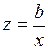
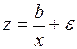
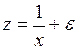
#Результатом линеаризации полиномиальных уравнений являются …
+линейные уравнения множественной регрессии
-нелинейные уравнения множественной регрессии
-линейные уравнения парной регрессии
-нелинейные уравнения парной регрессии
#Замена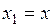 
; 
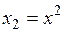подходит для уравнения …
+
- 
- 
- 
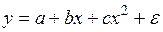
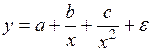
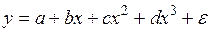
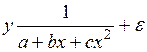
#Замена не подходит для уравнения …
+
- 
-
- 
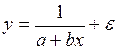
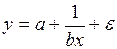
#Линеаризация не подразумевает процедуру …
+включения в модель дополнительных существенных факторов
-приведения нелинейного уравнения к линейному
-замены переменных
-преобразования уравнения
#Основной целью линеаризации уравнения регрессии является …
+возможность применения метода наименьших квадратов для оценки параметров
-улучшение качества модели
-повышение существенности связи между рассматриваемыми признаками
-получение новых нелинейных зависимостей
#Для нелинейных уравнений метод наименьших квадратов применяется к …
+преобразованным линеаризованным уравнениям
-не преобразованным линейным уравнениям
-обратным уравнениям
-нелинейным уравнениям
#Множественная регрессия не является результатом преобразования уравнения …
+ 
-
- 
-
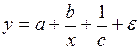
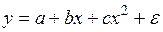
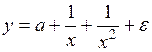
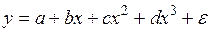
#К линейному виду нельзя привести …
+нелинейную модель внутренне линейную
-нелинейную модель внутренне нелинейную
-линейную модель внутренне нелинейную
-линейную модель внутренне линейную
#Величина коэффициента эластичности показывает …
+на сколько процентов изменится в среднем результат при изменении фактора на 1%
-во сколько раз измениться в среднем результат при изменении фактора в два раза
-предельно возможное значение результата
-предельно допустимое изменение варьируемого признака
#Спецификацию нелинейного уравнения парной регрессии целесообразно использовать, если значение…
+индекса детерминации, рассчитанного для данной модели достаточно близко к 1
-линейного коэффициента корреляции для исследуемой зависимости близко к 1
-индекса корреляции для исследуемой зависимости близко к 0
-доля остаточной дисперсии результативного признака в его общей дисперсии стремится к 1
#Если значение индекса корреляции для нелинейного уравнения регрессии стремится к 1, следовательно …
+нелинейная связь достаточно тесная
-линейная связь достаточно тесная
-нелинейная связь недостаточно тесная
-нелинейная связь отсутствует
#Оценить статистическую значимость нелинейного уравнения регрессии можно с помощью …
+критерия Фишера
-показателя эластичности
-средней ошибки аппроксимации
-линейного коэффициента корреляции
#Расчет средней ошибки аппроксимации для нелинейных уравнений регрессии связан с расчетом разности между …
+фактическим и теоретическим значениями результативной переменной
-фактическим и теоретическим значениями независимой переменной
-прогнозным и теоретическим значениями результативной переменной
-прогнозным и теоретическим значениями независимой переменной
#Назовите показатель корреляции для нелинейных моделей регрессии.
+индекс корреляции
-линейный коэффициент корреляции
-индекс детерминации
-парный коэффициент линейной корреляции
#Смысл расчета средней ошибки аппроксимации состоит в определении среднего арифметического значения …
+отклонений ε, выраженных в процентах от фактических значений результативного признака
-теоретических значений результативного признака, выраженных в процентах от его фактических значений
! отклонений ε, выраженных в процентах от фактических значений независимой переменной
-теоретических значений результативного признака, выраженных в процентах от его фактических значений признака
#Значение индекса детерминации, рассчитанное для нелинейного уравнения регрессии характеризует …
+долю дисперсии результативного признака, объясненную нелинейной регрессией в общей дисперсии результативного признака
-долю дисперсии результативного признака, объясненную линейной регрессией в общей дисперсии результативного признака
-долю дисперсии результативного признака, необъясненную нелинейной корреляцией в общей дисперсии результативного признака
-долю дисперсии результативного признака, объясненную линейной корреляцией в общей дисперсии результативного признака
#При хорошем качестве модели допустимым значением средней ошибки аппроксимации является …
+5 – 7 %
-20 – 25 %
-90 – 95 %
-50 %
#Значение индекса корреляции рассчитанное для нелинейного уравнения регрессии характеризует …
+тесноту нелинейной связи
-тесноту линейной связи
-тесноту обратной связи
-тесноту случайной связи
#Величина отклонений фактических значений результативного признака от его теоретических значений представляет собой …
+ошибку аппроксимации
-ошибку корреляции
-значение критерия Фишера
-показатель эластичности