Запишем некоторые рассчитанные ранее параметры фильтра:
1) Допустимая неравномерность АЧХ в ПП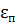 
:
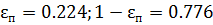
2) Допустимая неравномерность АЧХ в ПП 
:
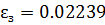
3) Значение нормированных граничных частот цифрового фильтра:
Рассчитаем параметр преобразования:
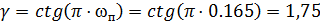
Определим граничную частоту полосы задерживания аналогового фильтра-прототипа:
Рассчитаем порядок фильтра:
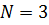
Найдем передаточную функцию аналогового фильтра прототипа:
Так как максимально допустимое ослабление в полосе пропускания
, то возьмем модуль коэффициента отражения 
По таблицам коэффициентов аналоговых фильтров найдем соответствующие коэффициенты:
По найденным значениям коэффициентов найдем передаточную функцию аналогового фильтра-прототипа:
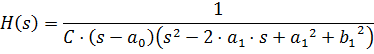
Проверим правильность рассчитанного порядка фильтра. Для этого найдем выражение комплексного коэффициента передачи аналогового фильтра 
:
Найдем модуль полученного выражения:
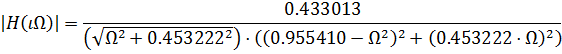
Подставим в полученное выражение 
граничные частоты полосы пропускания 
и полосы задерживания 
:
Таким образом, можно сделать вывод, что фильтр третьего порядка удовлетворяет требованиям задания к амплитудно-частотной характеристики проектируемого фильтра.
Расчет передаточной функции проектируемого цифрового фильтра методом билинейного преобразования
Используя метод билинейного преобразования для фильтра, найдем передаточную функцию ЦФ нижних частот по найденному выражению 
аналогового фильтра – прототипа.
Находим выражение передаточной функции цифрового фильтра 
= 
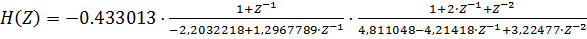
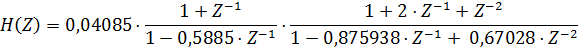
Таким образом, цифровой фильтр состоит из двух каскадов первого и второго порядков соответственно.
Контрольный расчет АЧХ фильтра в масштабах нормированных и реальных частот
Найдем выражение амплитудно-частотной характеристики цифрового фильтра, как модуль комплексного коэффициента передачи 
для этого используем замену 
в выражении H(Z).
Выполним преобразование по формуле Эйлера:
Далее найдем модуль передаточной функции и построим ее график:
1) В нормированных частотах
Рисунок 6.1 – АЧХ проектируемого фильтра в нормированных частотах.
2) В реальных частотах
Рисунок 6.2 – АЧХ проектируемого фильтра в реальных частотах.
Функции для задания «коридоров» и сами графики в логарифмическом масштабе представлены в приложении.
Проверка фильтра на устойчивость
Цифровой фильтр является устойчивым, если реакция фильтра на любое ограниченное воздействие так же будет ограничена. Чтобы фильтр был устойчивым необходимо выполнения требования 
, 
– полюсы.
Проверка фильтра на устойчивость может быть проведена по передаточной функции, для этого прировняем знаменатель к нулю:
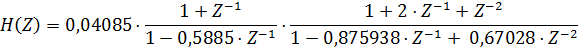
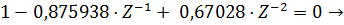
Все полюса фильтра меньше единицы, требования выполнены, следовательно, фильтр является устойчивым.