Теорема Ферма. Если дифференцируемая на промежутке X функция  достигает наибольшего или наименьшего значения во внутренней точке
достигает наибольшего или наименьшего значения во внутренней точке  этого промежутка, то производная функции в этой точке равна нулю, т.е.
этого промежутка, то производная функции в этой точке равна нулю, т.е. 
Доказательство. Пусть функция  дифференцируемая на промежутке X и в точке
дифференцируемая на промежутке X и в точке  принимает наименьшее значение (рис. 3.13).
принимает наименьшее значение (рис. 3.13).
 |
Рис. 3.13.
Тогда  если
если  и, следовательно, величина
и, следовательно, величина 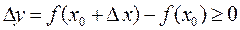 при достаточно малых
при достаточно малых 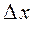 независимо от знака
независимо от знака 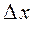 . Отсюда
. Отсюда  при
при  и
и  при
при 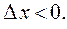 Переходя к пределу при
Переходя к пределу при  (справа) и при
(справа) и при  (слева), получим
(слева), получим  и
и 
По условию функция  дифференцируема в точке
дифференцируема в точке  , следовательно, ее предел при
, следовательно, ее предел при  не должен зависеть от способа стремления
не должен зависеть от способа стремления  (справа и слева), т.е.
(справа и слева), т.е. 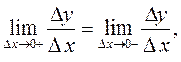 откуда следует, что
откуда следует, что 
Аналогично рассматривается случай, когда функция  принимает в точке
принимает в точке  набольшее значение.
набольшее значение.
Геометрический смысл теоремы Ферма очевиден: в точке наибольшего или наименьшего значения, достигаемого внутри промежутка X, касательная к графику функции параллельна оси абсцисс.
Теорема Ферма может быть использована для доказательства так называемых теорем о среднем, к рассмотрению которых мы переходим.
Теорема Ролля. Пусть функция  удовлетворяет следующим условиям:
удовлетворяет следующим условиям:
1) непрерывна на отрезке [ a, b ];
2) дифференцируема на интервале (a, b);
3) на концах отрезка принимает равные значения, т.е. 
Тогда внутри отрезка существует по крайней мере одна такая точка
 в которой производная функции равна нулю:
в которой производная функции равна нулю: 
Доказательство. Было установлено, что функция, непрерывная на отрезке, достигает на нем своего наибольшего M и наименьшего m значений. Если оба эти значения достигаются на концах отрезка, то по условию они равны (т.е. m=M), а это значит, что функция тождественно постоянна на отрезке [ a, b ]. Тогда производная равна нулю во всех точках этого отрезка. Если же хотя бы одно из этих значений – максимальное или минимальное – достигается внутри отрезка (т.е. m<M), то производная в соответствующей точке равна нулю в силу теоремы Ферма.
Отметим геометрический смысл теоремы Ролля (см. рис. 3.14) найдется хотя бы одна точка, в которой касательная к графику функции будет параллельна оси абсцисс; в этой точке производная и будет равна нулю (заметим, что на рис. 3.14 таких точек две: 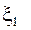 и
и  ).
).

Рис. 3.14
Если  , то теорему Ролля можно сформулировать так: между двумя последовательными нулями дифференцируемой функции имеется хотя бы один нуль производной.
, то теорему Ролля можно сформулировать так: между двумя последовательными нулями дифференцируемой функции имеется хотя бы один нуль производной.
Следует отметить, что все условия теоремы Ролля существенны и при невыполнении хотя бы одного из них заключение теоремы может оказаться неверным. Так, для функции, приведенных на рис. 3.15 нарушено только одно условие: на рис. 3.15а – непрерывность на отрезке [ a, b ], на рис. 3.15б - дифференцируемость на интервале (a, b), на рис. 3.15в – равенство значений 
В результате не существует такой точки  в которой
в которой 
 | |||||
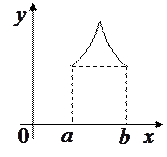 | |||||
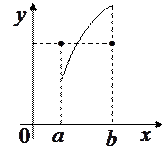 | |||||
а) б) в)
Рис. 3.15
Теорема Ролля является частным случаем теоремы Лагранжа.
Теорема Лагранжа. Пусть функция  удовлетворяет следующим условиям:
удовлетворяет следующим условиям:
1) непрерывна на отрезке [ a, b ];
2) дифференцируема на интервале (a, b);
Тогда внутри отрезка существует по крайней мере одна такая точка  в которой производная равна частному от деления приращения функции на приращение аргумента на этом отрезке, т.е.
в которой производная равна частному от деления приращения функции на приращение аргумента на этом отрезке, т.е.
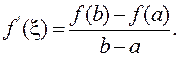 (3.14)
(3.14)
Доказательство. Введем новую функцию 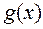 следующим образом:
следующим образом:
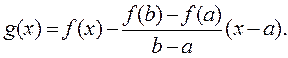
Функция 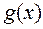 удовлетворяет условиям теоремы Ролля: она непрерывна на отрезке [ a, b ], дифференцируема на интервале (a, b) и принимает на его концах равные значения:
удовлетворяет условиям теоремы Ролля: она непрерывна на отрезке [ a, b ], дифференцируема на интервале (a, b) и принимает на его концах равные значения:

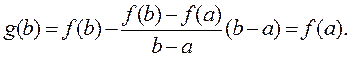
Следовательно, существует точка  такая, что
такая, что  или
или  откуда
откуда 
Заключение (3. 14) теоремы Лагранжа может быть записано и в виде:
 (3.15)
(3.15)
Выясним механический и геометрический смысл теоремы Лагранжа.
Приращение  - это изменение функции на отрезке [ a, b ];
- это изменение функции на отрезке [ a, b ];  средняя скорость изменения функции на этом отрезке; значение же производной в точке – это “мгновенная” скорость изменения функции. Таким образом, теорема утверждает: существует хотя бы одна точка внутри отрезка такая, что скорость изменения функции в ней равна средней скорости изменения функции на этом отрезке.
средняя скорость изменения функции на этом отрезке; значение же производной в точке – это “мгновенная” скорость изменения функции. Таким образом, теорема утверждает: существует хотя бы одна точка внутри отрезка такая, что скорость изменения функции в ней равна средней скорости изменения функции на этом отрезке.
Геометрическая интерпретация теоремы Лагранжа приведена на рис. 3.16

Рис. 3.16
Если перемещать прямую AB параллельно начальному положению, найдется хотя бы одна точка  в которой касательная к графику функции
в которой касательная к графику функции  и хорда AB, проведенная через концы дуги AB, параллельны так как угловой коэффициент секущей
и хорда AB, проведенная через концы дуги AB, параллельны так как угловой коэффициент секущей 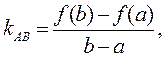 а касательной -
а касательной - 
Следствие. Если производная функции  равна нулю на некотором промежутке X, то функция тождественно постоянна на этом промежутке.
равна нулю на некотором промежутке X, то функция тождественно постоянна на этом промежутке.
Возьмем на рассматриваемом промежутке X отрезок [ a, x ].Согласно теореме Лагранжа 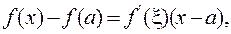 где
где  По условию
По условию  следовательно,
следовательно,  т.е.
т.е. 