Этот метод можно применять только к линейным уравнениям с постоянными коэффициентами и с правой частью специального вида:
,
где α, β – постоянные,
Pn (x), Qm (x) – многочлены степени n и m соответственно.
В этом случае в зависимости от конкретного вида правой части f (x) и корней характеристического уравнения частное решение y ч.н. следует искать в одной из следующих форм.
Сводная таблица видов частных решений
для различных видов правых частей
| № | Правая часть дифференциального уравнения | Корни характеристического уравнения | Виды частного решения |
| I | Pm (x) | 1. Число 0 не является корнем характеристического уравнения | 
|
| 2. Число 0 – корень характеристического уравнения кратности s | 
| ||
| II |
| 1. Число α не является корнем характеристического уравнения | 
|
| 2. Число α является корнем характеристического уравнения кратности s |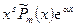 
| ||
| III |
| 1. Числа  не являются корнями характеристического уравнения
| 
|
| 2. Числа являются корнями характеристического уравнения кратности s
| 
| ||
| IV |
| 1. Числа  не являются корнями характеристического уравнения
| 
|
| 2. Числа являются корнями характеристического уравнения кратности s
| 
|
Первые три вида правых частей являются частными случаями IV вида.
В связи с ограниченным объемом рассмотрение уравнений более высоких порядков осталось за рамками данного пособия. Самостоятельно ознакомиться с данными видами уравнений можно, например, в пособии [5], указанного в списке литературы.
Примеры.
1. Найти общее решение уравнения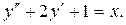 
Решение. Заданное уравнение является линейным дифференциальным уравнением второго порядка с постоянными коэффициентами и с правой частью специального вида. Перепишем уравнение в виде 
.
Запишем соответствующее однородное уравнение: 
Характеристическое уравнение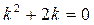 
, имеет корни 
.
Общее решение: 
Правая часть имеет вид 
, где 
(совпадает с корнем характеристического уравнения), 
- многочлен первой степени, поэтому частное решение следует искать в виде
, тогда
.
Подставив 
, 
, 
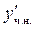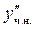в заданное уравнение и находим значение А, В методом неопределённых коэффициентов. (приравнивая коэффициенты при одинаковых степенях x в левой и правой части уравнения)
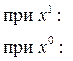
тогда 
Итак, по теореме
для нашего уравнения
2. Найти общее решение уравнения 
.
Решение. Запишем соответствующее однородное уравнение 
.
Тогда характеристическое уравнение 
имеет корни 
.
Общее решение:
Правая часть имеет вид:
, т.е. 
- многочлен первой степени. Числа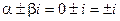 
не являются корнями характеристического уравнения.
Частное решение ищем в виде:
Подставив 
в исходное уравнение и приравняв коэффициенты при одинаковых функциях (т.е. использовав метод неопределённых коэффициентов) получаем:
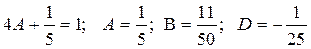
Частное решение:
Общее решение исходного уравнения:
.
Пример. Найти общее решение уравнения
.
Решение. Характеристическое уравнение 
имеет корни 
, а поэтому общим решением y о.о. соответствующего однородного уравнения будет
.
Для нахождения частного решения данного уравнения найдем частные решения двух уравнений
, (1)
(2)
Уравнение (1) имеет частное решение y 1 вида 
(см. табл. 1, случай II (1)). Подставляя выражение для y 1 в уравнение (1), найдем А =1, так что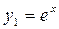 
. Частное решение уравнения (2) ищем в виде 
(см. табл. 1, случай II (2)). Находим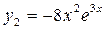 
.
В силу принципа суперпозиции решений частное решение y ч.н. исходного уравнения будет равно сумме частных решений y 1 и y 2 уравнений (1) и (2)
.
Общее решение уравнения
.