Требования к частоте и точности обсерваций.

Одного навигационного параметра, как бы точно измерен он ни был, для получения места судна недостаточно. Обсервованное место можно получить лишь при наличии не менее двух навигационных параметров, причем линии положения должны пересекаться под каким-то углом θ. Очевидно, что этот угол не может быть 180 или 0°, так как в этом случае линии положения сольются в одну и получить точку, определяющую место судна, будет невозможно. Наиболее благоприятным является положение, когда θ = 90°.

На рис.1 две линии положения (два пеленга) АР₁ и ВР₂ пересекаются под углом θ. В точке их пересечения получается место судна М₀. Если бы в наблюдениях пеленгов не было ошибок, то истинное место судна можно было бы считать в точке М₀. Но наличие неизбежных случайных и систематических ошибок в измерениях приводит к тому, что место судна определяется с ошибкой.

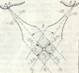рис.1

Рассмотрим ошибку в определении места судна под влиянием случайных ошибок. Так как появление противоположных по знаку случайных ошибок равновероятно, то равновероятно и смещение ∆n каждой линии положения первого и второго пеленгов (рис.1).

Под смещением изолинии понимают ее отклонение в ту или иную сторону от действительного положения, связанное с ошибками наблюдений навигационных параметров. Величину возможного смещения обычно характеризуют с помощью средней квадратической ошибки ± m. Так, величину смещения линии положения пеленга ∆n₁ на рис.1 можно определить по углу отклонения пеленга на величину средней квадратической ошибки ± m в измерении пеленга данным наблюдателем и расстоянию D от ориентира A до точки М₀.

∆n = ±Dm,

где m выражено в радианах.

Переходя к градусной мере, найдем ∆n = ± Dm | 57,3°

В общем случае смещение любой линии положения может быть найдено по формуле:

∆n = ± (m /g)

где g — коэффициент пропорцио­нальности, или градиент.

Итак, если найдены по средней квадратической ошибке наблюдения ± m смещения каждой линии положения ± ∆n, то оценить ошибку определения места судна можно площадью aba₁b₁ (рис.1). Вероятность нахождения места судна внутри такого эллипса невелика и составляет 39%. Для практических целей и для удобства анализа точности обсервации це­лесообразнее оценивать полученное место судна с помощью средней квадратической ошибки обсервации (точки).

Средняя квадратическая ошибка (иногда ее называют круговой) для оценки точности обсервации по двум линиям положения может быть вычислена по формуле

М = ± —— √ ∆n₁² + ∆n₂², (64)

sin θ

где М — радиус окружности, в площади которой находится вероят­ное место судна;

θ — угол пересечения изолиний (или линий положения); ∆n₁ — величина смещения первой линии положения, кб или ми­ли; ∆n₂ — величина смещения второй линии положения.

В теории ошибок доказывается, что вероятность нахождения мес­та судна в круге радиусом М равна 63—68% в зависимости от величины угла θ, т. е. достаточно высока.

Недостатком оценки точности определения места судна методом средней квадратической ошибки М является то, что она не дает представления о распределении ошибок по направлению. Преимущество заключается в простоте расчетов.

Для упрощения вычислительной работы судоводителя в условиях мостика созданы специальные таблицы и номограммы, с помощью которых легко и быстро находят среднюю квадратическую ошибку М обсервованного места судна по соответствующим для данных линий положения аргументам.

Влияние систематических ошибок проявляется иначе. Ни величина, ни знак этих ошибок судоводителю не известны. Но если наблюдения навигационных параметров одного типа производились в равных условиях, то можно полагать, что систематические ошибки ∆n₁^′ и ∆n₂^′ в каждой из линий положения приблизительно одинаковы и по величине, и по знаку. Поэтому смещение линий положения будет происходить в одном направлении для обеих линий положения, что приведет к смещению обсервованного места в точку М₁ или в точку М₂ (рис.2). Из этого вытекает, что действие систематических ошибок определяется линейной величиной, а не площадью, как действие случайных ошибок.

Систематические ошибки, если они выявлены, легко исключить из наблюдений, но когда они не известны, то остается только предполагать или ожидать их наличия. Поэтому в дальнейшем будет рассматриваться оценка точности полученных обсерваций только в зависимости от случайных ошибок.

Предполагаемые систематические ошибки совместно со случайными в случае необходимости могут быть учтены графическим способом. Пусть в точке М₀ (рис.3) находится место судна, полученное по двум пеленгам. Если предполагаемая систематическая ошибка вызывает смещение линии положения ∆n₁^′, то смещение положения судна будет найдено в точках М₁ и М₂. Рассчитав среднюю квадратическую ошибку обсервованного места ± m в зависимости от случайных ошибок, из точек М₁ и М₂ как из центров проводят окружности радиусом R = ± М. После этого обводят полученные окружности плавной кривой и получают общую площадь вероятного места судна с учетом возможных систематических и случайных ошибок.

рис.2 и 3