Тема: Числовые и функциональные ряды.
Числовые ряды.
Пусть дана числовая последовательность чисел: 
Числовым рядом называется выражение
= 
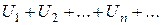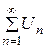, (1)
где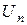 
- общий член ряда. Сумма Sn первых n членов ряда называется n - ой частичной суммой ряда: 
.
Ряд называется сходящимся, если существует конечный предел S последовательности его частичных сумм Sn при неограниченном возрастании номера n, то есть 
.
Предел S последовательности частичных сумм сходящегося ряда называется суммой ряда.
Если последовательность частичных сумм ряда не имеет предела, то ряд называется расходящимся. Расходящийся ряд суммы не имеет.
Геометрическая прогрессия: 
является сходящимся рядом при 
и расходящимся при 
.
Рассмотрим простейшие свойства сходящихся рядов.
1. Если ряд (43) сходится и имеет сумму S, то ряд образованный из произведений всех членов данного ряда на одно и тоже число l: 
, то же сходится и имеет сумму lS.
2. Если ряд (43) и ряд (2), то есть ряд 
, сходятся, то ряд, образованный сложением соответствующих членов данных рядов: 
, тоже сходится.
3. Если ряд (1) сходится, то сходится и ряд, полученный из данного отбрасыванием конечного числа членов.
Необходимый признак сходимости ряда. Если ряд (43) сходится, то общий член стремится к нулю при n ® ¥.
Стремление к нулю общего члена является необходимым, но не достаточным для сходимости ряда. Если Un не стремится к нулю, то ряд (43) расходится.
Пример 1. Доказать расходимость ряда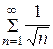 
.
Решение. Здесь 
- необходимое условие выполнено, но ряд расходится. Покажем это: 
. Так как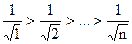 
, то 
. 
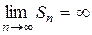, следовательно, ряд расходится.
Достаточные признаки сходимости положительных рядов.
Первый признак сходимости. Пусть даны два ряда (1) 
и
(2), причём каждый член ряда (2) не превосходит соответствующего члена pяда (2), то есть 
, n = 1,2… Тогда если сходится ряд (2), то сходится и ряд (1), ели расходится ряд (1), то расходится и ряд (2).
Рассмотрим вспомогательные ряды:
1) 
называется гармоническим. Он является расходящимся;
2) 
- обобщенный гармонический ряд, сходится при a > 1 и расходится при a £ 1.
Геометрическая прогрессия, гармонический и обобщенный гармонический ряд очень часто используется при исследовании рядов с помощью признаков сравнения.
Пример 2. Исследовать на сходимость ряд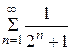 
.
Решение. 
, а ряд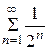 
- сходится, как геометрическая прогрессия. Следовательно, по первому признаку сходимости искомый ряд сходится.
Второй признак сходимости. Пусть даны два ряда (43) и
(44), если существует конечный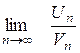 
¹ 0, то ряды (43) и (44) сходятся или расходятся одновременно.
Пример 3. Исследовать на сходимость ряд 
.
Решение. Рассмотрим вспомогательный ряд: 
- гармонический расходящийся ряд. Вычислим предел :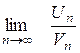
= 
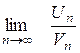¹0.
Значит, по второму признаку сходимости и данный ряд расходится.
Признак Даламбера. Если для знакоположительного ряда 
существует 
, то при D < 1 ряд сходится, а при D >1 ряд расходится. При D = 1 признак Даламбера вопрос о сходимости не решает.
Пример 4. Исследовать сходимость ряда 
.
Решение. Так как U n = 
, U n+1 = 
, то D = = 
< 1, поэтому данный ряд сходится по признаку Даламбера.
В тех случаях, когда признак Даламбера не позволяет сделать вывод о сходимости, применяют интегральный признак Коши:
Интегральный признак Коши. Пусть члены знакоположительного ряда (1) являются значениями при x = 1,2,3,…, n,.. некоторой функции f(x) положительной, непрерывной, убывающей на интервале 
:
U1 = f(1), U2 = f(2),…, Un = f (n).
Тогда: а) если 
- сходится, то сходится и ряд (43);
б) если - расходится, то ряд (43) также расходится.
Пример 5. Исследовать на сходимость ряд 
.
Решение. Если применить признак Даламбера, то 
, сказать о сходимости или расходимости нельзя. Применим интегральный признак Коши: 
- lnln3 = ¥. Несобственный интеграл расходится, а значит, расходится и данный ряд по интегральному признаку сходимости.
Признак Коши. Если для ряда (1) существует 
, то этот ряд сходится при C<1 и расходится при C >1.
Пример 6. Исследовать на сходимость ряд 
.
Решение. Рассмотрим предел 
= 
< 1, следовательно, ряд сходится по признаку Коши.
Знакопеременный ряд – ряд, содержащий как положительные, так и отрицательные члены.
Знакочередующийся ряд – ряд, в котором за каждым положительным членом следует отрицательный, а за каждым отрицательным членом положительный:
(3)
Для знакочередующихся рядов имеет место достаточный признак сходимости Лейбница.
Признак Лейбница. Если в знакочередующемся ряде (45) абсолютные величины членов убывают: 
и общий член ряда стремится к нулю: 
, то ряд сходится, причём его сумма положительна и не превосходит первого члена ряда.
Пример 7. Исследовать на сходимость ряд.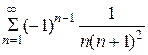 
.
Решение. Данный ряд является знакочередующимся, поэтому применяем признак Лейбница:
1) 
;
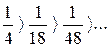2) 
. Оба условия выполнены, значит, ряд сходится по признаку Лейбница.
Сходящийся ряд называется условно сходящимся, если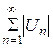 
- расходится.
Пример 8. Исследовать на условную и абсолютную сходимость:
а) 
; б) 
.
Решение. а) Рассмотрим ряд составленный из абсолютных величин, то есть ряд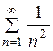 
. Он сходится, как обобщенный гармонический ряд, следовательно, искомый ряд сходится абсолютно.
б) Ряд составленный из абсолютных величин 
- расходится. Исследуем его на условную сходимость. Применим признак Лейбница:
1) 
;
2) 
.
Ряд сходится по признаку Лейбница, следовательно, искомый ряд сходится условно.
2. Функциональные и степенные ряды.
Ряд 
члены которого функции от x называется функциональным.
Совокупность значений x, при которых функции 
определены и ряд 
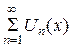- сходится, называется областью сходимости функционального ряда.
Каждому значению из области сходимости X соответствуют определенные значение величины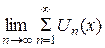 
. Эту величину являющейся функцией от x, называется суммой функционального ряда и обозначают S(x). Если функциональный ряд сходится и имеет сумму S(x), то разность 
- называется n-ым остатком функционального ряда.
Степенным рядом называется ряд вида
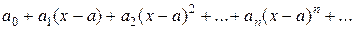(4)
где a и коэффициенты ряда 
- постоянные, в частности при a =
= 0 Þ 
(5)
Теорема. Областью сходимости степенного ряда 
является интервал (-R, R), к которому, в зависимости от конкретных случаев могут быть добавлены концевые точки –R и R.
Интеграл 
называется интервалом сходимости степенного ряда, а половина его длины, т.е. число R – радиусом сходимости, который можно вычислить по формуле:
(6)
А интервал (а - R; a + R) является интервалом сходимости ряда (46). Областью сходимостью степенного ряда является интервал сходимости плюс концевые точки интервала, если в них сходится ряд.
Пример 9. Найти область сходимости степенного ряда 
.
Решение. Находим интервал сходимости по формуле (6):
= 
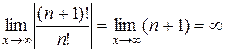. Значит, область сходимости степенного ряда 
вся числовая прямая.
Пример 10. Найти область сходимости степенного ряда 
.
Решение. Находим интервал сходимости по формуле (6):
= 
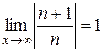, следовательно, интервалом сходимости данного ряда является интервал (1-1;1+1) = (0;2). Исследуем сходимость на концах интервала.
1) при х = 0 получаем знакочередующийся ряд 
, который сходится по признаку Лейбница: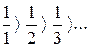 
и 
.
2) при х = 2 получаем гармонический ряд 
, который является расходящимся.
Значит, 
- область сходимости данного степенного ряда.