ДОКАЗАТЕЛЬСТВО. Пусть 
Тогда переменную 
можно представить в виде
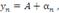
где 
– бесконечно малая величина.
Очевидно, что
Поскольку 
представляет собой бесконечно малую величину, то число c A является пределом последовательности 
:
ДОКАЗАТЕЛЬСТВО. Пусть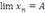 
и 
. Тогда переменные 
и 
можно представить в виде
где 
и 
– некоторые бесконечно малые величины.
Тогда
Учитывая, что 
- бесконечно малая величина, получаем
Аналогично,
Осталось распознать в выражении 
бесконечно малую величину, что влечет за собой
Далее покажем, что отношение 
можно представить в виде
Очевидно, что
где
Следовательно,
13. Функция вещественной переменной (определение). Действия над функциями вещественного аргумента.
Если задано правило, согласно которому каждому элементу множества x ставится в соответствие единственный элемент множества y, то говорят, что задана ФУНКЦИЯ, действующая из множества xв множество y.
Числовую величину Х назовем переменной величиной, если она может принимать различные значения. Каждому элементу Х сопоставлен единственный элемент У. Функция определена, если задано: 1) ООФ. 2) мнж-во У. 3) Правило сопоставления элементов У элементам Х.
СПОСОБЫЗАДАНИЯ: 1) Табличный-ф-ция задается таблицей ряда значений аргумента и соотв. им. знач-ям ф-ции. 2) Графический-график функции: знач-я ф-ции У, соответствующие значениям Х нах-ся непосредственно из графика. (+) наглядность. (-) неточность. 3) Описательный. 4)Аналитический. ф-ция задается в виде одной или нескольких формул, это наиболее совершенный способ задания функции.
ДЕЙСТВИЯ НАД ФУНКЦИЯМИ
Функции можно складывать
Функции можно умножать
Функции можно делить
Функции могут быть составлены друг с другом
16. Определение предела функции на языке последовательностей. Понятие об одностороннем пределе.
Постоянное число А называется предел функции f(x) при x→a, если для всякой последовательности {xn} значений аргумента, стремящейся к а, соответствующие им последовательности {f(xn)} имеют один и тот же предел А.
ОДНОСТОРОННИЕ ПРЕДЕЛЫ
Число А1 называется правосторонним пределом функции f(х) при х→хо+0
если для любого ε>0, найдется δ>0, что для всех хϵ(хо;хо+δ) выполняется │ f(х)-А1│<ε
Аналогично находится предел слева. Если сущ. предел f(х) в точке хо и он=А, то и сущ оба односторонних предела, причем А=А1=А2
18. Число e (б/д). Второй замечательный предел.
ЧИСЛОМ E называется предел последовательности
Известно, что число e является иррациональным числом e=2,718281828459045
ВТОРОЙ ЗАМЕЧАТЕЛЬНЫЙ ПРЕДЕЛ
14. Обратная функция. Монотонные функции. Элементарные функции. Понятие четности функции, ограниченности функции.
обратная функция: Пусть задана функция у=f(х) с обл. опр-я D и множ-вом знач. E. Если каждому знач-ю уϵЕ соотв. единственное знач-е хϵD, то опреде-ла ф-ция х=φ(у) с обл. опр-я Е и множ-вом знач-ий D. Такая ф-ция φ(у) называется обратной к f(х).
монотонность f(х1) <f(х2)-возрастающая, f(х1)≤f(х2)-неубывающая, f(х1)>f(х2)-убывающая, f(х1)≥f(х2)-невозрастающая.
Ограниченность: функцию у=f(х), определенную на множ-ве D называют ограниченной, если на этом множ-ве сущ. такое число М>0, что для всех х из D выполняется │f(х)│≤М
ЭЛЕМЕНТАРНЫЕ ФУНКЦИИ- функции, полученные при помощи конечного числа действий.
четность: четная: f(-х) =f(х), нечетная:f(-х)=-f(х)
22. Свойства функций вещественного аргумента, непрерывных в точке (б/д). Непрерывность элементарных функций.
СВОЙСТВА: 1) если 2 ф-ции опр-ны в некот. окр-ти точки хо и непрерывны в ней, то их сумма и произведение так же непрерывны в точке хо, а частное при условии,что ф-ция не=0.
2)Суперпозиция 2х ф-ций непрерывных в хо и уо также непрерывна в хо
3) Элементарные ф-ции непрерывны во всех точках своей области определения, в окрестностях которых они определены.
НЕПРЕРЫВНОСТЬ ЭЛЕМЕНТАРНЫХ ФУНКЦИЙ
1. f(x) = C, (где С – постоянная) непрерывна на R, т.к. 
при любом x.
2. f(x) = x, непрерывна на R, т.к.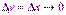 
при 
.
3. f(x) = sin(x), f(x) = cos(x)
7. f(x) = arcsin(x), f(x) = arccos(x), f(x) = arctg(x), f(x) = arcctg(x), непрерывны на своей области определения.
8. 
, где r – рациональное. П
9. 
, a > 1, непрерывна на R.
10. Логарифмическая функция непрерывна.
15. Определение предела функции на языке ε- δ (различные случаи (определения 1-4)) (в точке, на + и -бесконечности, конечный и бесконечный пределы).
Пусть ф-ция f(х) опр в некоторой окрестности точки хо кроме быть может самой точки хо.
КОНЕЧНЫЙ ПРЕДЕЛ В ТОЧКЕ
Число А называется пределом f(х) в точке х=хо при х стремящемуся к хо lim f(х)=δ, если для любого ε>0 найдется такое δ>0 что для всех х не равных хо удовлетворяющих │х-хо│<δ, выполняется условие │f(х)-а│<ε
КОНЕЧНЫЙ ПРЕДЕЛ НА БЕСКОНЕЧНОСТИ
Число А называется пределом f(х) при х→∞, если для любого ε>0 найдется такое δ>0, что для всех х таких, что │х│>δ выполняется │f(х-А)│<ε
Бесконечный предел в конечной точке
Предел f(х)=∞ в точке х=хо при х→хо. если для любого ε>0 найдется такое δ>0, что для всех х не равных хо удовл: │х-хо│<δ выполняется │f(х)│>ε
БЕСКОНЕЧНЫЙ ПРЕДЕЛ НА БЕСКОНЕЧНОСТИ
Предел f(х)=∞ при х→∞, если для любого ε>0 найдется такое δ>0, что для всех х таких что │х│>δ выполняется │f(х)│>ε
17. Первый замечательный (тригонометрический) предел (д).
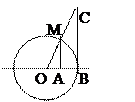
. Док-во: возьмём единичную окружность. Угол МОВ=х 0<x<p/2. площадь треугольника МОВ меньше, чем площадь сектора МОВ и меньше, чем площадь треугольника СОВ. |MA|=sin x=MA/OB=MA/1, |CB|=tgx=СB/OB.
S∆MOB=1/2 OB*AM. S сект=1/2 R2α
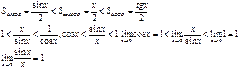
19. Бесконечно большие и бесконечно малые функции.
1) Функция f(x) - БЕСКОНЕЧНО БОЛЬШАЯ ФУНКЦИЯ, если ее предел в точке хо при х→хо =∞
если для любого ε>0 найдется такое δ>0, что для всех х на равных хо, таких что │х-хо│<δ выполняется │f(x)│>ε
2) Функция f(x) - БЕСКОНЕЧНО БОЛЬШАЯ ФУНКЦИЯ, если ее предел при х→∞ =∞
если для любого ε>0 найдется такое δ>0, что для всех х, таких что │х│>δ выполняется │f(x)│>ε
СВОЙСТВА ББФ
1. Произведение б.б.ф. на функцию, предел которой отличен от 0, есть б.б.ф.
2. Сумма б.б.ф. и ограниченной функции есть б.б.ф.
3. Частное от деления б.б.ф. на функцию, имеющую предел, есть б.б.ф.
Функция f(х) называется БЕСКОНЕЧНО МАЛОЙ, если ее предел при х→хо равен 0, если для любого ε>0 найдется такое δ>0, что для всех х таких что │х-хо│<δ выполняется │f(х)│<ε
СВОЙСТВА БМФ
1. Алгебраическая сумма конечного числа бесконечно малых функций есть бесконечно малая функция.
2. Произведение ограниченной ф-ции на б.м. ф-цию есть б.м. функция
3. Произведение двух б.м. есть б.м. функция.
4. Произведение б.м. ф-ции на число есть б.м. функция.
5. Если f(х) б.м. ф-ция, то 1\ f(х)-б.б. ф-ция и наоборот
6. Частное от деления б.м.ф на функцию, имеющую отличный от 0 предел, есть б.м.ф.
СВЯЗЬ БЕСКОНЕЧНО МАЛЫХ И БЕСКОНЕЧНО БОЛЬШИХ ФУНКЦИЙ
Связь: 1. Если a(x) бмф, то 1/a(x) ббф
2 Если b(x) ббф, то 1/b(x) бмф
Док-во: Пусть а(х) – бмф при х->x0, те lim a(x)(при х->x0)=0. Тогда д/люб. Е>0 сущ-ет б>0 д\люб. х: 0<|x-x0|<б выполн. |a(x)|<E, т е |1/а(х)|>1/E, те |1/a(x)|>M, где М=1/Е. А это означает, что ф-ция 1/а(х) – ббф. Аналогично доказывается обратное.
20. Свойства пределов функций, связанные с арифметическими операциями над функциями.
1. Предел суммы(разности) двух функций равен сумме(разности) их пределов.
2. Функция может иметь только один предел при х→хо
3. Предел произведения двух функций равен произведению их пределов.
4. Постоянный множитель можно выносить за знак предела.
5. Предел степени с натуральным показателем равен той же степени предела.
6. Предел дроби равен пределу числителя, деленному на предел знаменателя, если предел знаменателя не =0.
21. Непрерывность функции в точке. Классификация точек разрыва.
Пусть функция f(х) определена в точке хо и некоторой окрестности точки хо.
Ф-ция f(х) назыв. НЕПРЕРЫВНОЙ В ТОЧКЕ хо если сущ. предел ф-ции в этой точке и он равен значению ф-ции в этой точке. т.е выполняются 3 условия: 1) f(х) определена в хо и ее окрестности; 2) Сущ. предел ф-ции, равный односторонним пределам 3) предел = значению ф-ции в этой точке.
ТОЧКИ РАЗРЫВА
Точка разрыва 1 рода:
1) lim f(x) x→xo+o=lim f(x) x→xo-o точка устранимого разрыва, тогда возможно:
а) в точке хо f(х) не определена
б) в точке хо f(х) определена, но ее предел не равен значению ф-ции в этой точке
2) предел слева не равен пределу справа - точка скачка
Если хотя бы один из односторонних пределов не сущ. или =∞, то ф-ция имеет разрыв 2 рода.
23. Свойства функций, непрерывных на замкнутом промежутке (Т. 1-4) (б/д).
Ф-ция f(х) назыв. НЕПРЕРЫВНОЙ В ИНТЕРВАЛЕ (а;в) если она непрерывна в каждой точке этого интервала.
Ф-ция f(х) назыв. НЕПРЕРЫВНОЙ НА ОТРЕЗКЕ [a;в] если: 1) она непрерывна в каждой точке интервала (а;в); 2) в точке х=а непрерывна справа; 3) в т. х=в непрерывна слева.
ф-ция f(х) называется ограниченной на отрезке [a;b] если сущ. такое число с>0, что │f(х)│<с для всех х из [a;b].
1-АЯ ТЕОРЕМА ВЕЙЕРШТРАССА: всякая непрерывная на данном отрезке функция ограничена на этом отрезке.
2-АЯ ТЕОРЕМА ВЕЙЕРШТРАССА: если функция непрерывна на [a;b], то достигает не нем своего наибольшего и наименьшего значения.
3. Если функция непрерывна на [a;b] и на его концах принимает значения разных знаков, то внутри [a;b] найдется хотя бы одна точка С, в которой данная функция обращается в 0, то есть корень функции.
4. Если f(x) непрерывна на [a;b] и f(a)=A, f(b)=B, то для любого числа C(C>A, C<B) найдется такое c,что f(c)=C.
25. Уравнение касательной к графику функции.
Прямая у-уо=к(х-хо), угловой коэффициент которой равен значению производной в точке, называется КАСАТЕЛЬНОЙ к графику функции в точке(xo;f(xo)).
Рассмотрим секущую, проходящую через точку (xo;f(xo)) и (xo+∆х;f(xo+∆х)). При ∆х→0, т.е. секущая стремится занять положение касательной, говорят, что касательная это предельное положение секущей, следовательно, геометрический смысл производной состоит в том, что она равна угловому коэффициенту (тангенсу угла наклона) касательной в точке касания.
f'(xo)=k=tgα
y-yo=f'(xo)*(x-xo) ур-е касательной
Прямая, перпендикулярная касательной в точке касания, называется нормалью к кривой.
y-yo=-1\f'(xo)*(x-xo) ур-е нормали
24. Производная функции вещественного аргумента (определение, геометрический смысл).
ПРОИЗВОДНОЙ ФУНКЦИИ в точке называется предел отношения приращения функции к вызвавшему его приращению аргумента, если приращение стремится к 0(при условии, что этот предел существует)
y'=lim ∆f/∆x= lim f(x+xo)-f(xo)/∆x
Обратим внимание что предел может существовать и быть конечным, тогда говорят, что в данной точке функция имеет конечную производную. Если предел существует и бесконечен, тогда ф-ция им. бесконечную производную. Если предел не сущ., то и производная не сущ.
Функция, имеющая производную в каждой точке данного интервала назыв. ДИФФЕРЕНЦИРУЕМОЙ, а операция ее нахождения ДИФФЕРЕНЦИРОВАНИЕМ.
Существуют ОДНОСТОРОННИЕ ПРЕДЕЛЫфункции y=│x│ lim ∆y/∆x x→0-0 и lim ∆y/∆x x→0+0 и обозначаю f'_(x) и f'+(x). Если они не равны, то производная в точке не существует.
ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ
30. Производные элементарных функций (таблица производных).
26. Дифференцируемость функции одного аргумента. Теорема о связи между непрерывностью и дифференцируемостью (д).
y=f(x) называется дифференцируемой в точке хо если ее приращение ∆у можно представить в виде ∆у=А*∆х+g(∆x) * ∆x где А- независимое число, g(∆x)- б.м. ф-ция при ∆x→0
ТЕОРЕМА: чтобы y=f(x) была дифференцируема в точке хо необходимо и достаточно, чтобы она имела в этой точке конечную производную.
Доказательство: Необходимость
y=f(x) дифференцируема, значит имеет конечную производную и по определению ее приращение можно представить в виде ∆у=А*∆х+g(∆x) * ∆x│: ∆x
∆у/∆x=А+ g(∆x)
lim ∆у/∆x=lim А+ g(∆x) =A
Достаточность
Пусть у функции y=f(x) существует конечная производная. Докажем, что она дифференцируема.
lim (∆у/∆x-А) =0
g(∆x) =∆у/∆x-А│* ∆x
g(∆x) *∆x =∆у-А*∆x
∆у=А*∆х+g(∆x) * ∆x
27. Свойства операции дифференцирования (1-4) (д).
1)
2)
3)
4)
28. Производная сложной функции (д).
Пусть y=f(u) b u=g(x) y=f(g(x)) сложная функция с промежуточным аргументом u и независимым аргументом x.
ТЕОРЕМА
Пусть u=g(x) дифференцируема в точке хо, а y=f(u) дифференцируема в точке uo, где uo=g(xo), тогда сложная функция y=f(g(x)) имеет производную в точке хо, и справедлива формула:
y'(xo)=f'(uo)*g(xo)
Доказательство: По определению производной y'(xo)=lim f'(g(xo+∆x)) -f(g(xo))\∆x (∆x→0) т.к. ф-ция y=f(u) дифференцируема в точке uo и f'(uo)=limf(uo+∆u)-f(uo)/∆u
Применим теорему о существовании предела: если lim f(x)=a, f(x)=a+m(x).
f(uo+∆u)-f(uo)/∆u=a+m(∆u) │*∆u
f(uo+∆u)-f(uo)=(f"(uo)+ m(∆u)) * ∆u
т.к. u=g(x) f(uo+∆u)-f(uo)= f(g(xo+∆x)) -f(g(xo))
y'(xo)= limf(uo+∆u) * ∆u/∆x
y'(xo)= limf(uo+∆u) + lim ∆u/∆x
y'(xo)=f'(uo)*g(xo)
29. Производная обратной функции (д).
Пусть y=f(x) определена, строго монотонна и непрерывна в окрестности точки хо.
g=f-1(y) - обратная к ней. Тогда если y=f(x) имеет производную в точке хо, отличную от 0, то обратная функция также имеет в точке yo=f(xo) конечную не =0 производную, которую находят по формуле.
f-1'(yo)=1/f'(xo)
Доказательство: По определению производной f-1'(yo)=lim f-1(yo+∆y)-f-1(yo)/∆y= lim xo+∆x-xo/f(xo+∆x)-f(xo)=lim∆x/f(xo+∆x)-f(xo)
Переход на основании 2ого определения непрерывности функции
lim∆x/f(xo+∆x)-f(xo)= lim∆x/f(xo+∆x)-f(xo)* ∆x\∆x= lim 1/f(xo+∆x)-f(xo)\∆x=1/f'(xo)
31. Теорема Ролля (д)
Пусть на отрезке [a;b] определена ф-ция y=f(x), причем выполняются условия: 1) она непрерывна на отрезке [a;b]; 2) она дифференцируема на интервале (a;b); 3) f(a)=f(b); тогда существует точка С принадлежащая интервалу (a;b) и f'(c)=0.
ДОКАЗАТЕЛЬСТВО: Так как функция y=f(x) непрерывна на отрезке [a;b], то по теореме Вейерштрасса она имеет на этом отрезке наибольшее значение М и наименьшее значение m, т.е. существуют точки х1 и х2 принадлежащие [a;b] и f(x1)=M, f(x2)=m и m≤f(x)≤M. Возможны 2 случая:
1) M=m
в этом случае функция является постоянной и f'(x)=0 в любой точке этого интервала.
2) m<M
т.к. согласно условию f(a)=f(b), то хотя бы одно из значений m или M не принимается на концах отрезка, т.е. сущ. точка С принадлежащая интервалу (a;b) в кот-ой ф-ция принимает наибольшее или наименьшее значение, т.к. ф-ция дифференцируема в этой точке, то по теореме Ферма следует, что f'(c)=0.
32. Теорема Лагранжа (д).
Пусть на отрезке [a;b] определена ф-ция y=f(x), причем выполняются условия: 1) она непрерывна на отрезке [a;b]; 2) она дифференцируема на интервале (a;b); тогда существует точка С принадлежащая интервалу (a;b) и f'(c)=f(b)-f(a)/(b-a)
Доказательство:
Рассмотрим на отрезке [a;b] вспомогательную функцию F(x)= f(x)-f(a)-f(b)-f(a)/(b-a), для кот-ой выполняются все условия теоремы Ролля: 1) Она непрерывна на отрезке как разность двух функций; 2) Дифференцируема, т.к. существует производная f'(x); 3) f(a)=f(b). Значит существует точка С принадлежащая интервалу (a;b) такая что F'(c)=0 следовательно
f'(c)=F'(c)- f(b)-f(a)/(b-a) f'(c)=f(b)-f(a)/(b-a) - формула конечных приращений
Замечание: геометрический смысл теоремы Лагранжа состоит в том, что на графике функции y=f(x) найдется точка с координатами (с;f(c)), в которой касательная к графику функции будет параллельна секущей ab.
33. Теорема Коши (д).
ТЕОРЕМА. Пусть функции 
и 
непрерывны в замкнутом промежутке 
; дифференцируемы в открытом промежутке 
; 
в открытом промежутке 
. Тогда существует такая точка 
, что
|
ДОКАЗАТЕЛЬСТВО. Заметим, что 
. В противном случае – согласно теореме Ролля – производная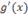 
обратилась бы в нуль в некоторой точке 
Рассмотрим вспомогательную функцию
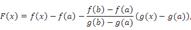
которая удовлетворяет всем условиям теоремы Ролля и, в частности, принимает одинаковые значения на концах промежутка 
:
Тогда существует точка 
, в которой
34. Правило Лопиталя (д).
Теорема: Пусть f(x) и g(x) определены и дифференцируемы в некоторой окрестности точки хо, за исключением, быть может, самой точки хо, известно так же что пределы этих функций равны 0. Тогда, если существует предел отношения производных этих функций, конечный или бесконечный, то существует и предел отношения самих функций и справедливо:
lim f(x)/g(x)=lim f'(x)/g'(x) при x→xo
Доказательство: предположим, что f(x) и g(x) непрерывны в точке хо. Применим теорему Коши для отрезка [x;xo].
f(x)-f(xo)/g(x)-g(xo)=f'(c)/g'(c) cϵ(x;xo)
по условию непрерывности f(xo)=g(xo)=0
f(x)/g(x)=f'(c)/g'(c) перейдем к пределу при х→хо учитывая, что с→хо
lim f(x)/g(x)=lim f'(c)/g'(c)
по условию существования предела отношения производных обозначим lim f'(х)/g'(х) числом L, тогда lim f'(c)/g'(c)= L, следовательно lim f(x)/g(x)=lim f'(c)/g'(c)=L тогда справедливо limf(x)/g(x)=lim f'(х)/g'(х)
35. Дифференциал функции (определение, геометрический смысл).
Пусть y=f(x) дифференцируема в точке хо, тогда ее приращение ∆у можно представить в виде суммы 2х слагаемых ∆у=А*∆х+g(∆x)* ∆x, где g(∆x)- бесконечно малая функция при ∆x→0. Рассмотрим слагаемое А*∆х, оно является бесконечно малым одного порядка с ∆х.
lim А*∆х/∆х=A не = 0
Рассмотрим 2ое слагаемое g(∆x)* ∆x, оно явл. б. малым более высокого порядка чем ∆x
lim g(∆x)* ∆x/∆x= lim g(∆x)=0, то есть А не =0 является главной частью приращения y=f(x). ДИФФЕРЕНЦИАЛОМ функции y=f(x) в точке хо называется главная линейная относительно ∆x часть приращения ф-ции в этой точке dу=A*∆x. Если А=0, то и в этом случает полагают что A*∆x является главной частью приращения и dу=0. Учитывая, что А=f'(xo) получаем dу=f'(xo)*∆x
ГЕОМЕТРИЧЕСКИЙ СМЫСЛ
Дифференциал функции y=f(x) в точке хо равен приращению ординаты касательной к графику функции в этой точке, когда хо получит приращение ∆x.