Законы распределения дискретных случайных величин.

Лекция 2. Вероятностные характеристики дискретных случайных величин.

План.

1.Вероятностные характеристики событий.

2.Законы распределения дискретных случайных величин.

3.Моменты дискретных случайных величин.

4.Вероятностные числовые характеристики дискретных случайных величин.

5.Интегральный закон распределения.

Вероятностные характеристики событий.

К категории случайных событий можно отнести такие, точное предска­зание протекания которых в каждом отдельном случае оказывается невоз­можным.

Так, например, если бросать монету, то выпадение герба или цифры будет случайным событием. Если повторить этот эксперимент N раз, то можно зафиксировать определенное число выпадений герба т и число выпадений цифры N-т. Относительная величина m/N называется частотой события выпадения герба, а величина (N-m)/N — частотой события выпадения цифры.

Рис 2.1.

Если устремить число экспериментов N→ ∞, то частоты событий будут стремиться к некоторому пределу

, (2.1)

называемому вероятностью данного события.

В рассмотренном случае очевидно, что обе вероятности выпадения герба и цифры одинаковы и равны 0,5.

Вероятность каждого события лежит в интервале 0≤ Р ≤1.

Если событие является невозможным, вероятность его равна нулю; если событие является достоверным, его вероятность равна единице.

В примере с бросанием монеты рассматривалась дискретная случайная величина, которая могла принимать два фиксированных значения — выпадение герба и выпадение цифры. Существуют случайные величины, которые могут принимать непрерывные значения. Так, например, если рассмотреть стрельбу из орудия (рис 2.1), то расстояние L от орудия до места падения снаряда будет случайной величиной, которая на определенном отрезке может принимать все возможные значения. В этом случае можно говорить о вероятности нахождения случайной величины L в некотором интервале от L ₁ до L ₂.

Законы распределения дискретных случайных величин.

Чтобы полностью знать дискретную случайную величину, надо иметь следующие данные:

а) все возможные значения, которые она может принимать при данных условиях задачи или опыта;

б) вероятность появления каждого из этих значений. Так, например, если дискретная случайная величина может принимать конечное число значений х₁, х₂, x₃.... x_n и вероятность каждого значения будет соответственно P₁, P₂, P₃.... P_n, то можно представить так называемый закон распределения случайной величины в виде таблицы. При этом должно выполняться условие

(2.2)

Пусть, например, производится опыт бросания игральной кости. Очевидно, что при каждом бросании число выпавших очков, которое представляет собой случайную величину, может принимать одно из следующих значений: 1, 2, 3, 4, 5, 6. Если кость совершенно симметрична, то вероятность выпадения каждой из этих цифр является одинаковой. Так как число различных значений, которое может принимать случайная величина, равно шести, тоиз (2.2) имеем

Графически этот закон распределения изображен на рис. 2.2. Он представляет собой равновероятное распределение в некотором интервале (в рассматриваемом случае от 1 до 6).

В некоторых случаях закон распределения случайной величины может задаваться в аналитической форме.

Примером аналитического задания закона распределения дискретной случайной величины является часто используемый закон Пуассона. Он применим к дискретным случайным величинам, которые теоретически могут принимать все положительные значения от 0 до ∞.

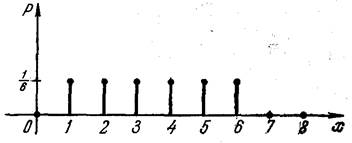
Рис 2.2.

Примерами таких величин могут служить число пассажиров вагона трамвая, число вызовов на телефонной станции в течение какого-либо определенного отрезка времени, число электронов, попадаю­щих на анод электронной лампы за определенный промежуток времени, и т. п. Этот закон записывается следующим образом для целых значений числа х:

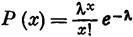(2.3)

где Р (х) — вероятность появления значения x; λ представляет собой среднее значение данной дискретной величины, полученное по результатам большого числа опытов.

Графически этот закон имеет вид, изображенный на рис.2.3, причем место максимума зависит от величины λ.

В качестве одного из примеров рассмотрим функцию у(t), котораяможет принимать одно из значений +а или -a (рис. 2.4).

Предположим, что среднее число перемен знака в единицу времени этой функции равно у. и что вероятность перемены знака на интервале (t, t + Dt) не зависит от того, что происходит в остальные моменты времени. Тогда вероятность перемены знака на интервале Dt составит mDt<<1.

Рис 2.3.

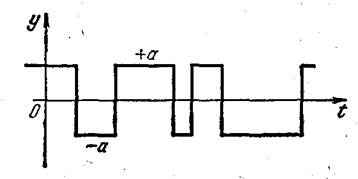
Рис. 2.4

Вероятность того, что на интервале Dt не произойдет перемены знака, будет (1-mDt).

Если взять два интервала времени Dt, то вероятность отсутствия перемены знака на двух интервалах будет равна произведению вероятностей и составит (1-mDt) ². Для трех интервалов Dt она составит (1-mDt) ³ и т. д.

Возьмем теперь конечный интервал времени T, который можно представить в виде T = пDt. Тогда вероятность отсутствия перемены знака на этом интервале можно найти из выражения

(2.4)

Аналогичным образом можно показать, что вероятность одной перемены знака на интервале Т будет Р (1)= mTe^-mT, вероятность двух перемен

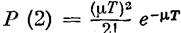(2.5)

и т. д. Следовательно, вероятность х перемен знака на интервале времени Т будет определяться выражением

(2.6)

которое совпадает с формулой (2.З), если положить в ней λ=mT, где mT — среднее число перемен знака на интервале времени Т, которое будет наблюдаться при многократном повторении наблюдения.

Хотя закон распределения полностью определяет случайную величину, для практики нужны некоторые более простые осредненные характеристики случайной величины, выражающиеся в виде обыкновенных неслучайных чисел.

Одной из таких характеристикявляется среднее значение, или математическое ожидание, случайной величины. Оно определяется из выражения

(2.7)

Так, например, для случая бросания игральной кости

Вообще для равновероятного закона распределения (11.5) превращается в формулу

(2.8)

Для случайной величины, распределенной по закону Пуассона, среднее значение, подсчитанное но формуле (2.5), дает

Основные свойства среднего значения случайной величины следующие.

1. Для любых случайных величин среднее значение их суммы равно. сумме средних значений этих величин:

2. Среднее значение произведения случайных величин, независимых друг от друга, равно произведению средних значений этих величин:

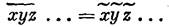
Последняя формула не распространяется на общий случай любых случайных величин.